A particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle θ above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection θ so that R is maximum ? What is the maximum value of R?
Refer to below given figure .
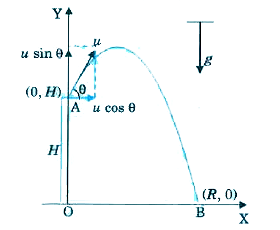
We have selected botton of the tower O as the origin . Horizontal direction is X-axis and vertically upward direction is selected as Y-axis A is the point of projection and B is the point where particle hits the ground . Coordinqates of the initial point a are (0. H) and for the final point (R, 0). components of displacement along X-axis and Y-axis can be written as followings:
Sx=R−0=R,
Sy=0−H=−H
Acceleration due to gravity is vertically downwards , hence components can be written as follows :
ax=0,
ay=−g,
Components of initial velocity are as follows :
ux=ucosθ,
uy=usinθ,
X-axis: Sx=uxt+12axt2
⇒=(ucosθ)t⇒t=Rucosθ
Y-axis: Sy=uyt+12ayt2
⇒−H=(usinθ)t+12(−g)t2
Substituting t from equation (i) , we get the following :
⇒−H=(usinθ)(Rucosθ)−g2(Rucosθ)2
⇒−H=Rtanθ−gR22u2(1+tan2θ)
⇒−2u2H=2u2Rtanθ−gR2(1+tan2θ)
⇒−2u2H=2u2Rtanθ−gR2−gR2−gR2tan2θ
⇒gR2tan2θ−2u2Rtanθ+(gR2−2u2H)=0
Discriminate of above equation must be greater than zero for real value of tan θ .
Δ≥0
⇒4u4R2−4gR2(gR2−2u2H)≥0
⇒u4−g(gR2−2u2H)≥0
⇒u4−g2R2+2gu2H≥0
⇒g2R2≤u4+2gu2H
⇒R≤ug√u2+2gH
Hence maximum range can be written as followings:
⇒Rmax=ug√u2+2gH
If discriminant of a quadratic equation ax2+bx+c=0 is zero , then equal roots can be written as x=−b/2a . If we assume R equal to Rmax described by equation (ii), then we can understand that discriminant of the equation (ii) will be zero , hence tanθ for the equation can be written as follows:
tanθ=2Ru22gR2=u2gR
Substituting value of R from equation (iii) , we get the following :
tanθ=u2g(u)g√u2+2gH
⇒tanθ=u√u2+2gH
⇒θ=tan−1(u√u2+2gH)
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)
25 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) (NCERT (Additional Exercises))
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Conceptual Questions
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
View SolutionA stone is projected at an angle α to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot α from the foot of the lower.
View Solution
Knowledge Check
A ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
Av0√3gB√3v0gCv0gDv0gA particle just clear a wall of height b at a distance a and strikes the ground at a distance from the point of projection, the angle of projection is :
Atan−1(bac)B45∘Ctan−1(bca(c−1))Dtan−1(bca)A particle is projected in air with an initial velocity u directed at an angle θ above horizontal. After time t0 the velocity of the particle is directed at angle ϕ above horizontal.
AAt time t0 magnitude of verticle component of velocity of the particle is ucosθcotϕBAt time t0 magnitude of rate of change of speed of the particle is gsinϕCThe radius of curvature of the trajectory at time t0 is u2cos2θgcos3ϕDThe value of time t0 is ucosθ(tanθ−tanϕ)/g.
A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
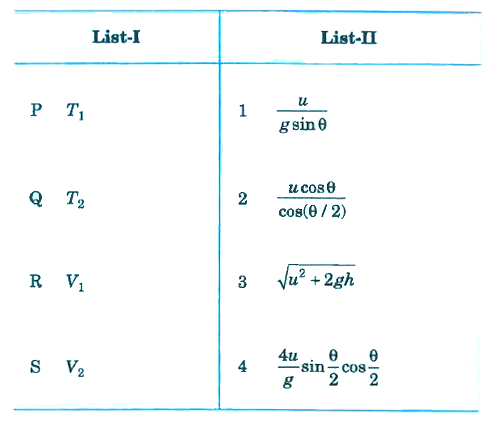
View SolutionA particle is projected from the top of a tower of height h with a speed u at an angle θ above the horizontal .
T1=Time taken by the projectile to reach the height of tower again .
T2=Time taken by the projectile to move at right angle to initial direction of motion .
V1=Speed of the projectile when it moves at an angle θ/2 with the horizontal .
V2=Speed with projectile strikes the ground .
.
View SolutionA particle is projected from ground with some initial velocity making an angle of 45∘ with the horizontal. It reaches a height of 7.5m above the ground while it travels a horizontal distance of 10m from the point of projection. The initial speed of the projection is
View SolutionA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View Solution
