Particle projected from tower fo heigh 10m as shown in figure. Find the time (in sec) after which particle will hit the ground.
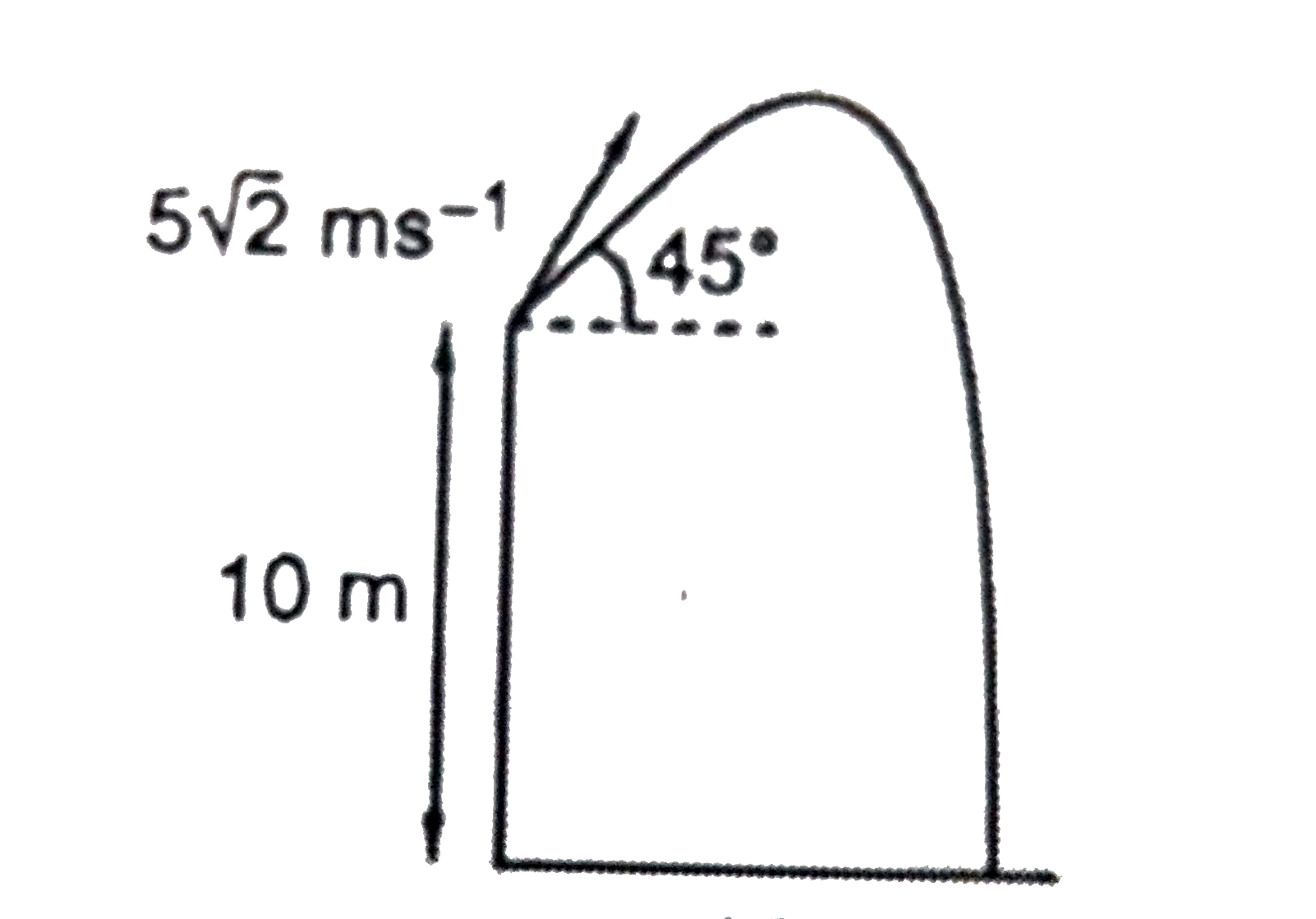
The correct Answer is:2
uy=vsin45∘=5√2×1√2=5ms−1
Using, y=uyt+12ayt2
−10=5t+12(−10)t2
t2−t=2=0
(r−2)(t+1)=0
∴ t=2 (rejecting -ve time)
Topper's Solved these Questions
Similar Questions
In the figures shown, three particles are thrown from a tower of height 40 m as shown in figure. In each case find the time when the particles strike the ground and the distance of this point from foot of the tower.
, 
, 
.
View SolutionA particle is projected at an angle 60∘ with speed 10√3 m/s from the point A as shown in the figure. At the same time the wedge is made to move with speed 10√3 m/s toward right as shown in figure. Find the time after which particle will strike the wedge.
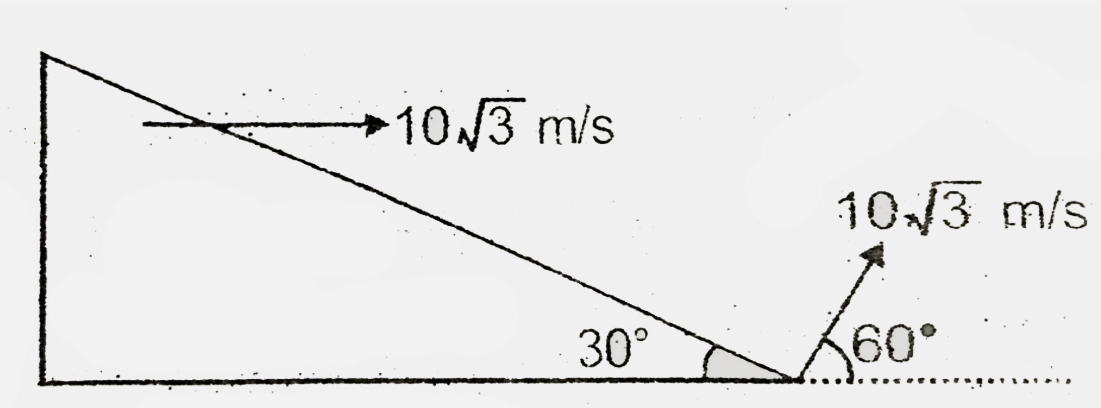
View Solution
Knowledge Check
A particle is projected at an angle 60∘ with speed 10(√3)m/s, from the point A, as shown in the figure. At the same time the wedge is made to move with speed 10(√3)m/s towards right as shown in the figure. Then the time after which particle will strike with wedge is
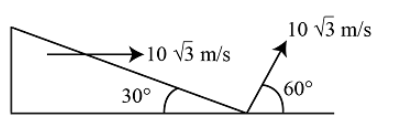A2 sB2(sqrt3) sC4√3sDNone of theseTwo particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
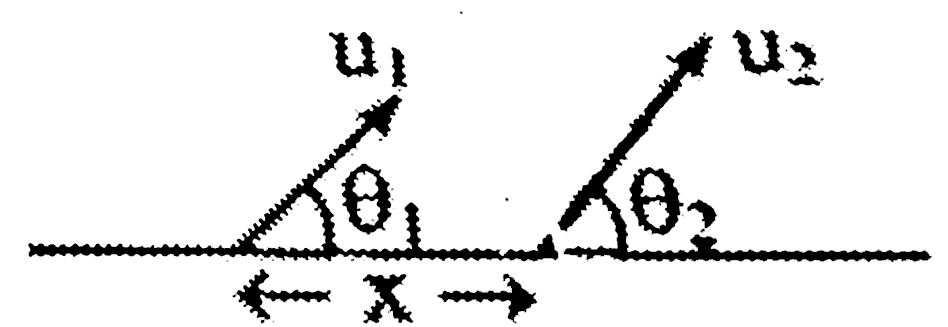Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
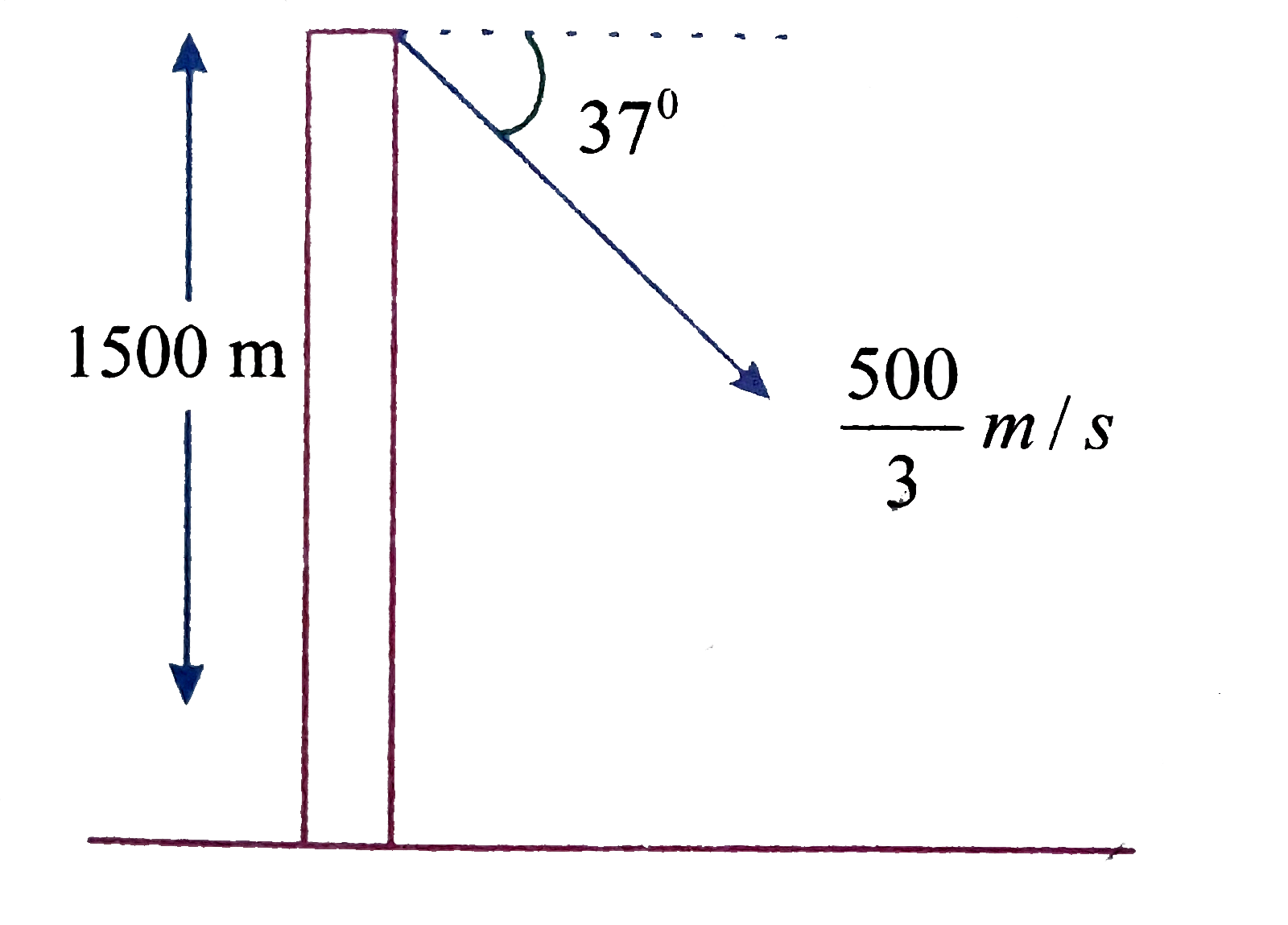
A particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
View SolutionFive particles are projected simultaneously from the top of a tower that is h=32m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal.
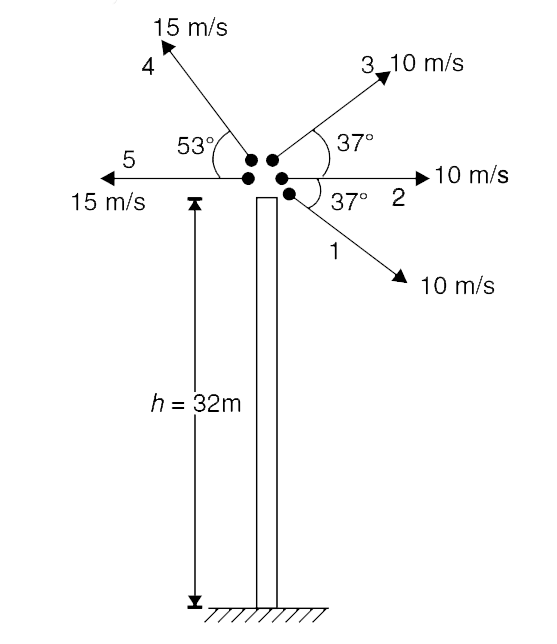
(a) Which particle will hit the ground first?
(b) Separation between which two particles is maximum at the instant the first particle hits the ground?
(c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground.
[g=10m/s2,tan37∘=34]
View SolutionA particle is projected from a tower of height 25 m with velocity 20√2m/s at 45∘. Find the time when particle strikes with ground. The horizontal distance from the foot of tower where it strikes. Also find the velocity at the time of collision.
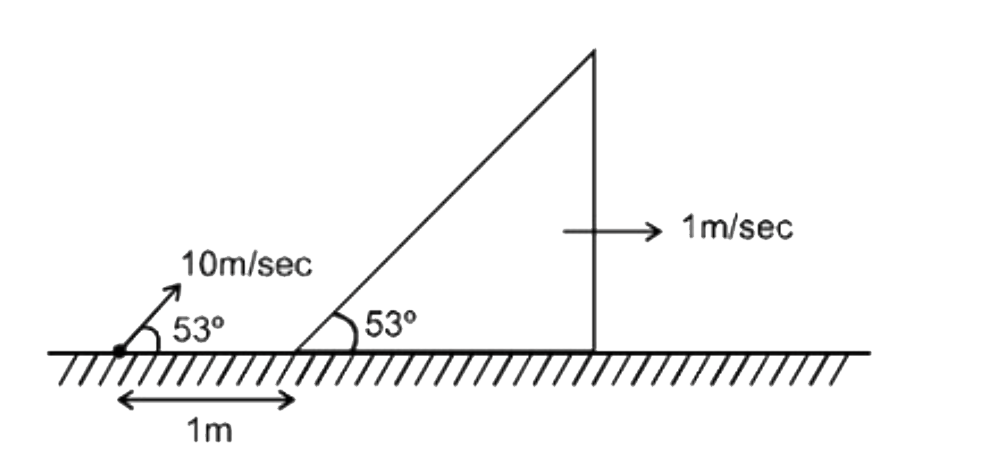
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]
View SolutionA particle is dropped from the top of a tower of height 80m. Find the time of jurney and the speed with which it strikes the ground.
View SolutionTwo particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
.
View Solution