Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

P2
P1
P1(V02)λ(V02+Ax)λ
P2(V02)λ(V02+Ax)λ
The correct Answer is:C
Step by step video, text & image solution for Following figure shows on adiabatic cylindrical container of volume V_(0) divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (C_(p)//C_(y)=lambda) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
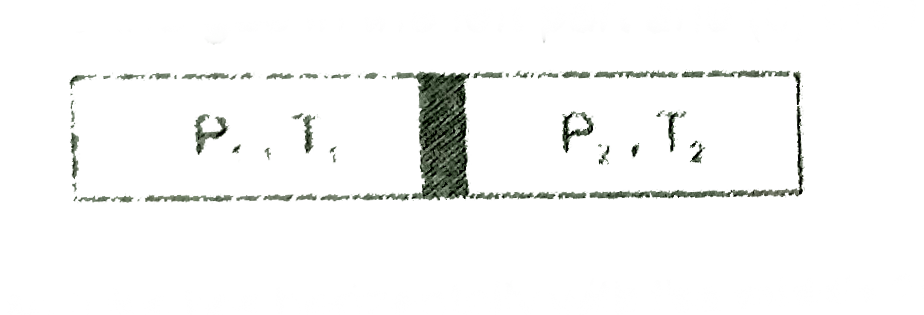
View SolutionShow a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
View Solution
Knowledge Check
In an adiabatic change, the pressure p and temperature T of a diatomic gas are related by the relation p∝Tα, where α equals
A(a) 1.67B(b) 0.4C(c) 0.6D(d) 3.5A closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston isAP0γA2xV0B2P0γA2xV0C3P0γA2xV0DP0γA2x(γ−1)V0In an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
A35B53C25D52
Figure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

View SolutionA cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
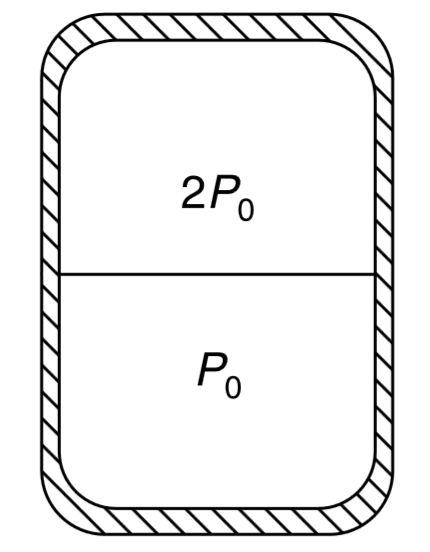
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
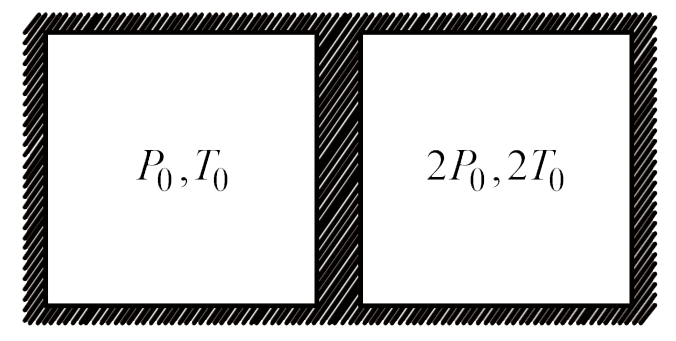
The pressure in left compartment after thermal equilibrium is achieved is
View SolutionIn an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
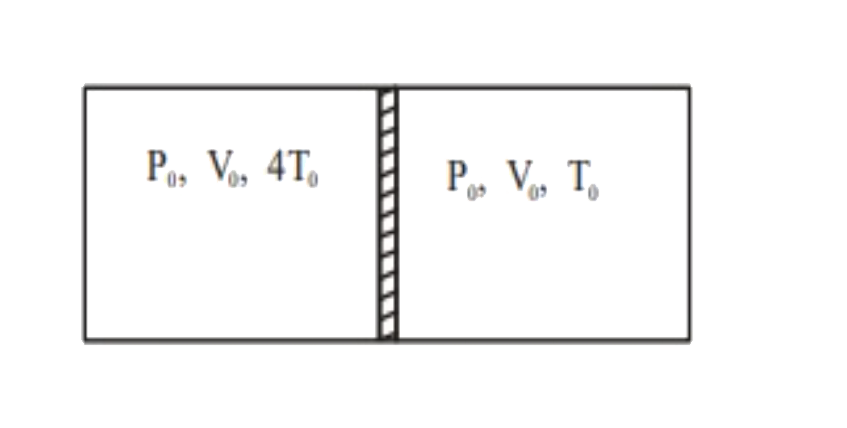
View Solution
