For a particle moving in a straight line
If velocity is negative and acceleration is positive then speed increases.
if velocity is positive and acceleration is negative then speed decreases.
if velocity is zero at an instant then acceleration must also be zero at that instant.
it is possible that speed of a particle is never zero in an interval of time, but average speed is zero.
The correct Answer is:b
To solve the problem regarding the motion of a particle in a straight line and determine which statement is correct, we will analyze each option based on the principles of physics related to velocity and acceleration.
1. Understanding the Concepts:
- Velocity: It is the rate of change of displacement and can be positive or negative, indicating the direction of motion.
- Acceleration: It is the rate of change of velocity. It can also be positive or negative, indicating whether the velocity is increasing or decreasing.
2. Analyzing Each Statement:
- Statement A: "If velocity is negative, acceleration is positive, then speed increases."
- If velocity is negative and acceleration is positive, the particle is moving in the negative direction while accelerating in the positive direction. This means the speed (magnitude of velocity) is decreasing. This statement is incorrect.
- Statement B: "If velocity is positive, acceleration is negative, speed decreases."
- If velocity is positive and acceleration is negative, the particle is moving in the positive direction but slowing down. Hence, the speed is indeed decreasing. This statement is correct.
- Statement C: "If velocity is zero at an instant, then the acceleration must be zero at that instant."
- This is not necessarily true. For example, when an object is thrown upwards, its velocity becomes zero at the highest point, but the acceleration due to gravity is still acting downwards (non-zero). This statement is incorrect.
- Statement D: "It is possible when the speed of the particle is never zero in an interval of time, but the average speed is zero."
- Average speed is defined as total distance traveled divided by total time taken. If the speed is never zero, the average speed cannot be zero. This statement is incorrect.
3. Conclusion:
- The only correct statement among the options provided is Statement B: "If velocity is positive, acceleration is negative, speed decreases."
- Velocity: It is the rate of change of displacement and can be positive or negative, indicating the direction of motion.
- Acceleration: It is the rate of change of velocity. It can also be positive or negative, indicating whether the velocity is increasing or decreasing.
- Statement A: "If velocity is negative, acceleration is positive, then speed increases."
- If velocity is negative and acceleration is positive, the particle is moving in the negative direction while accelerating in the positive direction. This means the speed (magnitude of velocity) is decreasing. This statement is incorrect.
- If velocity is positive and acceleration is negative, the particle is moving in the positive direction but slowing down. Hence, the speed is indeed decreasing. This statement is correct.
- This is not necessarily true. For example, when an object is thrown upwards, its velocity becomes zero at the highest point, but the acceleration due to gravity is still acting downwards (non-zero). This statement is incorrect.
- Average speed is defined as total distance traveled divided by total time taken. If the speed is never zero, the average speed cannot be zero. This statement is incorrect.
- The only correct statement among the options provided is Statement B: "If velocity is positive, acceleration is negative, speed decreases."
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( D.(MULTIPLE CHOICE QUESTIONS))
9 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (ASSERTION REASON)
9 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
74 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
Knowledge Check
Select the correct statement. For a particle moving on a straight line
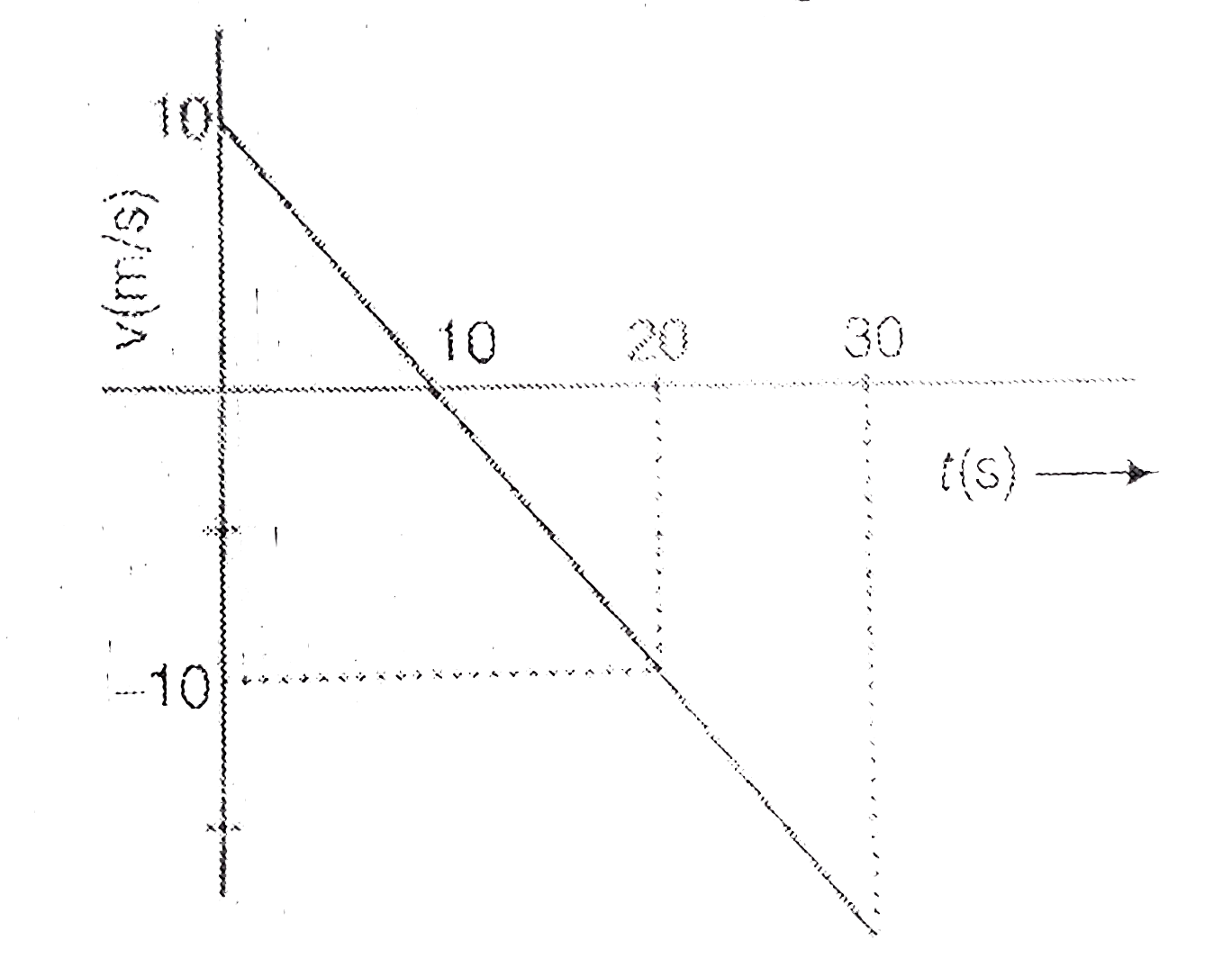
AAverage speed is equal to magnitude of average velocityBAverage speed may be greater than magnitude of average velocityCAverage velocity = instantaneous velocity if velocity is constantDMoving with constant acceleration, average velocity for given time interval is arithmetic mean of initial and final velocityThe velocity-time plot for a particle moving on a straight line is shown in figure.
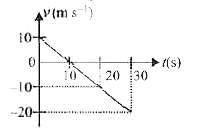AThe particle has a constant acceleration.BThe particle has never tumed around.CThe particle has zero displacement.DThe average speed in the interval 0 to 10 s is the same as the average speed in the interval 10s to 20 s.Velocity displacement graph of a particle moving in a straight line is as shown in figure.
Amagnitude of acceleration of particle is decreasingBmagnitude of acceleration of particlre is increasingCacceleration versus displacement graph straight lineDacceleration versus displacement graph is parabola
The velocity-position graph of a particle moving in a straight line along x -axis is givenbelow.Acceleration of particle,at x=2m is
View SolutionThe velocity- time plot for a particle moving on a straight line is shown in the figure
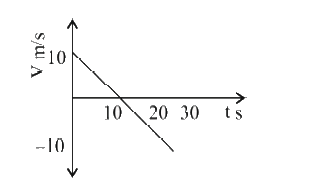
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
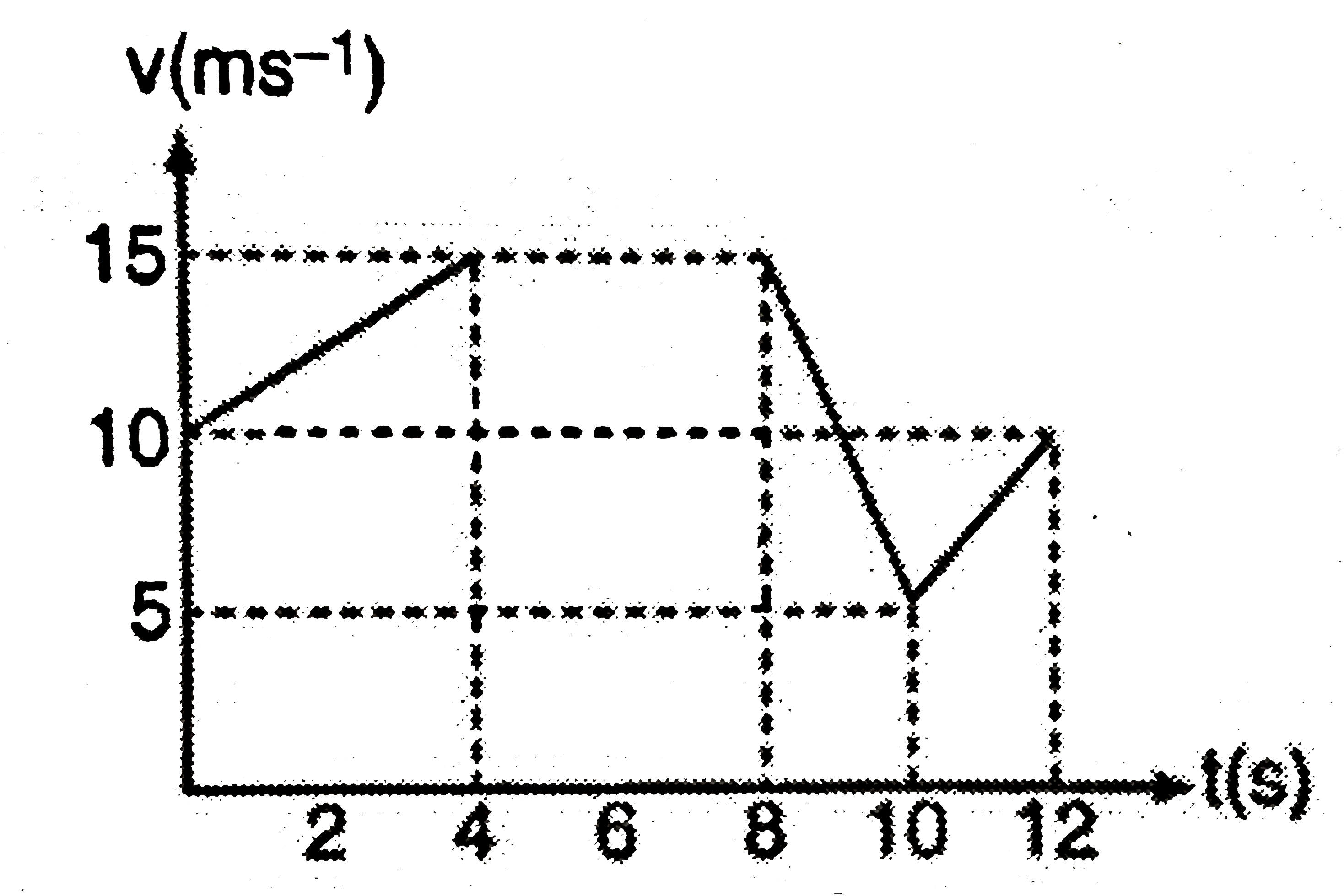
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View Solution