For an ideal gas the equation of a process for which the heat capacity of the gas varies with temperatue as C=(α/T(α) is a constant) is given by
VlnT=constant
VT1/(γ−1)_(e)α/RT=constant
V1γ−1Tα/RT=constant
Vγ−1T=constant
The correct Answer is:B
ΔQ=dU+PdV
⇒αTdT=CVdT+PdV⇒αTdT=CVdT+RTVdV
αdTT=Rγ−1dT+RTdVV
⇒αRdTT2=1γ−1adTt+dVV
On integrating and soliving
VT1/(γ−1)α/(RT)e=constant
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - MCQs
6 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Carnot Engine
9 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The specific heat of an ideal gas varies with temperature T as
AT1BT2CT−2DT0Two moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process isA1P=V0T3/204RT52e(T−T0T0)B1P=V0T3/202RT52e(T−T0T0)C1P=V0T3/204RT52e(T+T0T0)D1P=V0T3/203RT52e(T−T0T0)A monoatomic ideal gas undergoes a process ABC. The heat given to the gas is
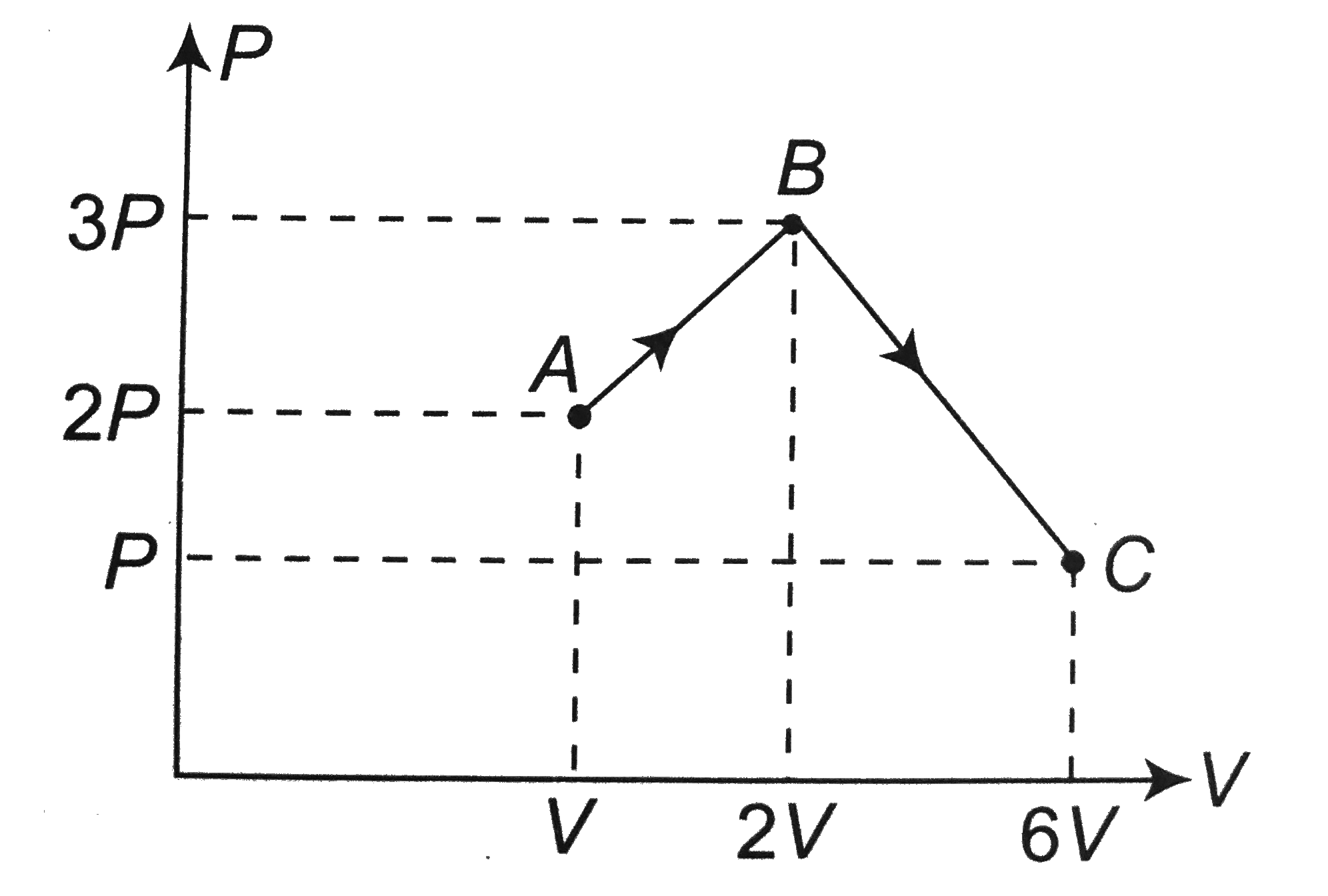 A7.5PVB12.5PVC16.5PVD20.5PV
A7.5PVB12.5PVC16.5PVD20.5PV
For the case of an ideal gas find the equation of the process (in the variables T,V) in which the molar heat capacity varies as :
(a) C=CV+αT ,
(b) C=CV+βV,
( c) C=Cv+ap ,
where α,β and a are constants.
View SolutionOne mole of an ideal gas with heat capacity CV goes through a process in which its entropy S depends on T as S=α/T, where α is a constant. The gas temperature varies from T1 to T2 Find :
(a) the molar heat capacity of the gas as function of its temperature ,
(b) the amount of heat transferred to the gas ,
( c) the work performed by the gas.
View SolutionAn ideal gas has an adiabatic exponent γ. In some process its molar heat capacity varies as C=α/T,where α is a constant Find :
(a) the work performed by one mole of the gas during its heating from the temperature T0 to the temperature η times higher ,
(b) the equation of the process in the variables p,V.
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionThe molar heat capacity for a gas at constant T and P is
View Solution
