For an ideal gas the slope of V-T graph during an adiabatic process is (dV)/(dT) = -matap∮wherevolumeandtemperatureareV_(0)andT_(0).F∈dthevalueofC_(p) of the gas. It is given that m is a positive number.
The correct Answer is:(mT0V0+1)
To solve the problem, we will follow these steps:
Step 1: Understand the Adiabatic Process for an Ideal Gas
In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas, the relationship between volume (V), temperature (T), and pressure (P) can be described using the adiabatic condition.
Step 2: Use the Adiabatic Condition
The adiabatic condition for an ideal gas can be expressed as:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
Step 3: Differentiate the Adiabatic Condition
To find the slope of the V-T graph, we need to express the relationship between volume and temperature. We can differentiate the equation PVγ=constant with respect to T.
Using the ideal gas law PV=nRT, we can express pressure P in terms of V and T:
P=nRTV
Substituting this into the adiabatic condition gives:
nRTVVγ=constant
Step 4: Find the Slope
We are given that the slope of the V-T graph is:
dVdT=−m
At the point where V=V0 and T=T0, we can express this as:
dVdT=dVdT∣∣∣(V0,T0)=−m
Step 5: Relate the Slope to Heat Capacities
From thermodynamic relations, we know:
dVdT=−V0T0(γ−1)
Setting this equal to −m:
−m=−V0T0(γ−1)
Thus, we have:
m=V0T0(γ−1)
Step 6: Solve for Cp
We know that:
γ=CpCv
And since Cv=Cp−R, we can express γ as:
γ=CpCp−R
Substituting this into our equation gives:
m=V0T0(CpCp−R−1)
Simplifying this leads to:
m=V0T0(RCp−R)
Rearranging gives:
Cp=mT0V0R+R
Final Expression for Cp
Thus, the final expression for Cp is:
Cp=mT0V0R+R
In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas, the relationship between volume (V), temperature (T), and pressure (P) can be described using the adiabatic condition.
The adiabatic condition for an ideal gas can be expressed as:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
To find the slope of the V-T graph, we need to express the relationship between volume and temperature. We can differentiate the equation PVγ=constant with respect to T.
P=nRTV
Substituting this into the adiabatic condition gives:
nRTVVγ=constant
We are given that the slope of the V-T graph is:
dVdT=−m
At the point where V=V0 and T=T0, we can express this as:
dVdT=dVdT∣∣∣(V0,T0)=−m
From thermodynamic relations, we know:
dVdT=−V0T0(γ−1)
Setting this equal to −m:
−m=−V0T0(γ−1)
Thus, we have:
m=V0T0(γ−1)
We know that:
γ=CpCv
And since Cv=Cp−R, we can express γ as:
γ=CpCp−R
Substituting this into our equation gives:
m=V0T0(CpCp−R−1)
Simplifying this leads to:
m=V0T0(RCp−R)
Rearranging gives:
Cp=mT0V0R+R
Thus, the final expression for Cp is:
Cp=mT0V0R+R
Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 2
34 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
Knowledge Check
A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature (V0,T0). From the details given in the graph, find the value of adiabatic constant γ
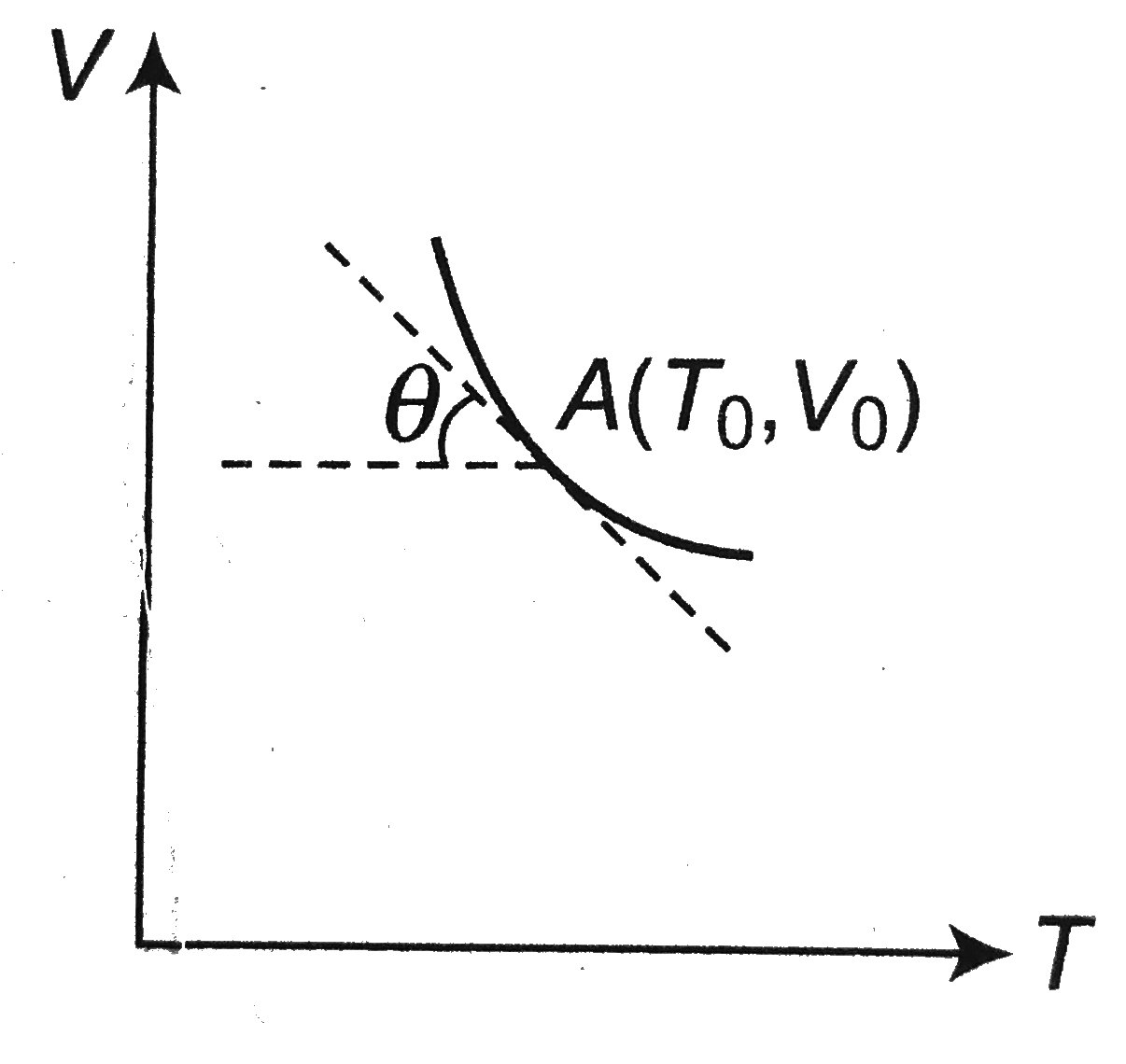 AV0T0tanθ+1BV0tanθT0+1CV0tan2θT0+1DV0T0+tanθ
AV0T0tanθ+1BV0tanθT0+1CV0tan2θT0+1DV0T0+tanθDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature. The ratio of CPCV for the gas is
A53B32C43D2During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature the ratio CpCv for the gas is
A2B53C32D43
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio CP/CV for the gas is
View SolutionA gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are V0,T0 and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
View SolutionP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
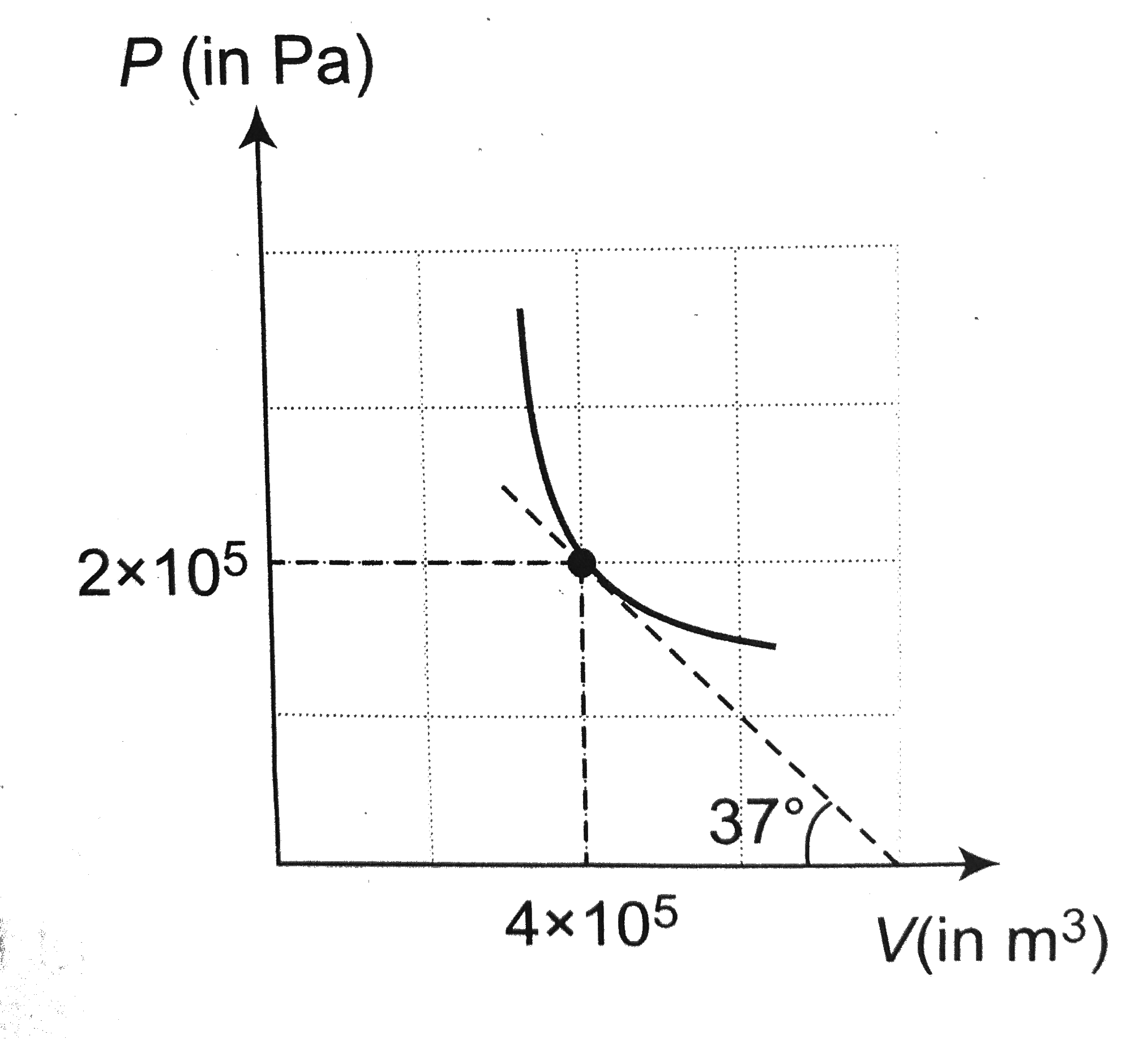
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View Solution
