A gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are $V_{0}, T_{0}$ and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]

A

$\frac{m R T_{0}}{V_{0}}$

B

$\frac{M R T_{0}}{2 V_{0}}$

C

$\frac{(V_{0} + m T_{0}) R}{V_{0}}$

D

$\frac{(V_{0} + m T_{0}) R}{2 V_{0}}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem step by step, we will analyze the adiabatic process of the gas and derive the expression for the molar specific heat at constant pressure $C_{p}$ .
Step 1: Understand the Adiabatic Process
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure $P$ , volume $V$ , and temperature $T$ for an ideal gas undergoing an adiabatic process is given by:
$P V^{γ} = constant$
where $γ = \frac{C_{p}}{C_{v}}$ .
Step 2: Use the Ideal Gas Law
From the ideal gas law, we have:
$P V = n R T$
We can express $P$ in terms of $V$ and $T$ :
$P = \frac{n R T}{V}$
Step 3: Substitute into the Adiabatic Equation
Substituting $P$ into the adiabatic equation gives:
$(\frac{n R T}{V}) V^{γ} = C$
Simplifying this, we get:
$n R T V^{γ - 1} = C$
Step 4: Rearranging the Equation
Rearranging the equation, we find:
$T V^{γ - 1} = \frac{C}{n R} = C^{'}$
This shows the relationship between $T$ and $V$ during the adiabatic process.
Step 5: Differentiate the Equation
To find the slope of the $V - T$ graph, we differentiate the equation $T V^{γ - 1} = C^{'}$ with respect to $T$ :
$\frac{d}{d T} (T V^{γ - 1}) = 0$
Using the product rule:
$V^{γ - 1} + T (γ - 1) V^{γ - 2} \frac{d V}{d T} = 0$
Step 6: Solve for $\frac{d V}{d T}$
Rearranging gives:
$\frac{d V}{d T} = - \frac{V^{γ - 1}}{T (γ - 1) V^{γ - 2}} = - \frac{V}{T (γ - 1)}$
Thus, the slope of the $V - T$ graph is:
$∣ ∣ ∣ \frac{d V}{d T} ∣ ∣ ∣ = \frac{V}{T (γ - 1)}$
Step 7: Substitute Known Values
At the point where $V = V_{0}$ and $T = T_{0}$ , we have:
$m = \frac{V_{0}}{T_{0} (γ - 1)}$
Step 8: Express $γ$ in Terms of $C_{p}$ and $C_{v}$
Recall that:
$γ = \frac{C_{p}}{C_{v}}$
and
$C_{p} - C_{v} = R$
Thus, we can express $γ - 1$ as:
$γ - 1 = \frac{C_{p} - R}{C_{v}}$
Step 9: Solve for $C_{p}$
Substituting this back into our equation for $m$ :
$m = \frac{V_{0}}{T_{0} (\frac{C_{p} - R}{C_{v}})}$
Rearranging gives:
$C_{p} = \frac{R V_{0}}{T_{0} m} + R$
Step 10: Final Expression for $C_{p}$
Thus, we can express $C_{p}$ as:
$C_{p} = \frac{R (V_{0} + m T_{0})}{V_{0}}$
Conclusion
The molar specific heat at constant pressure $C_{p}$ is given by:
$C_{p} = R \frac{V_{0} + m T_{0}}{V_{0}}$

Updated on:18/9/2024

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature $(V_{0}, T_{0})$ . From the details given in the graph, find the value of adiabatic constant $γ$

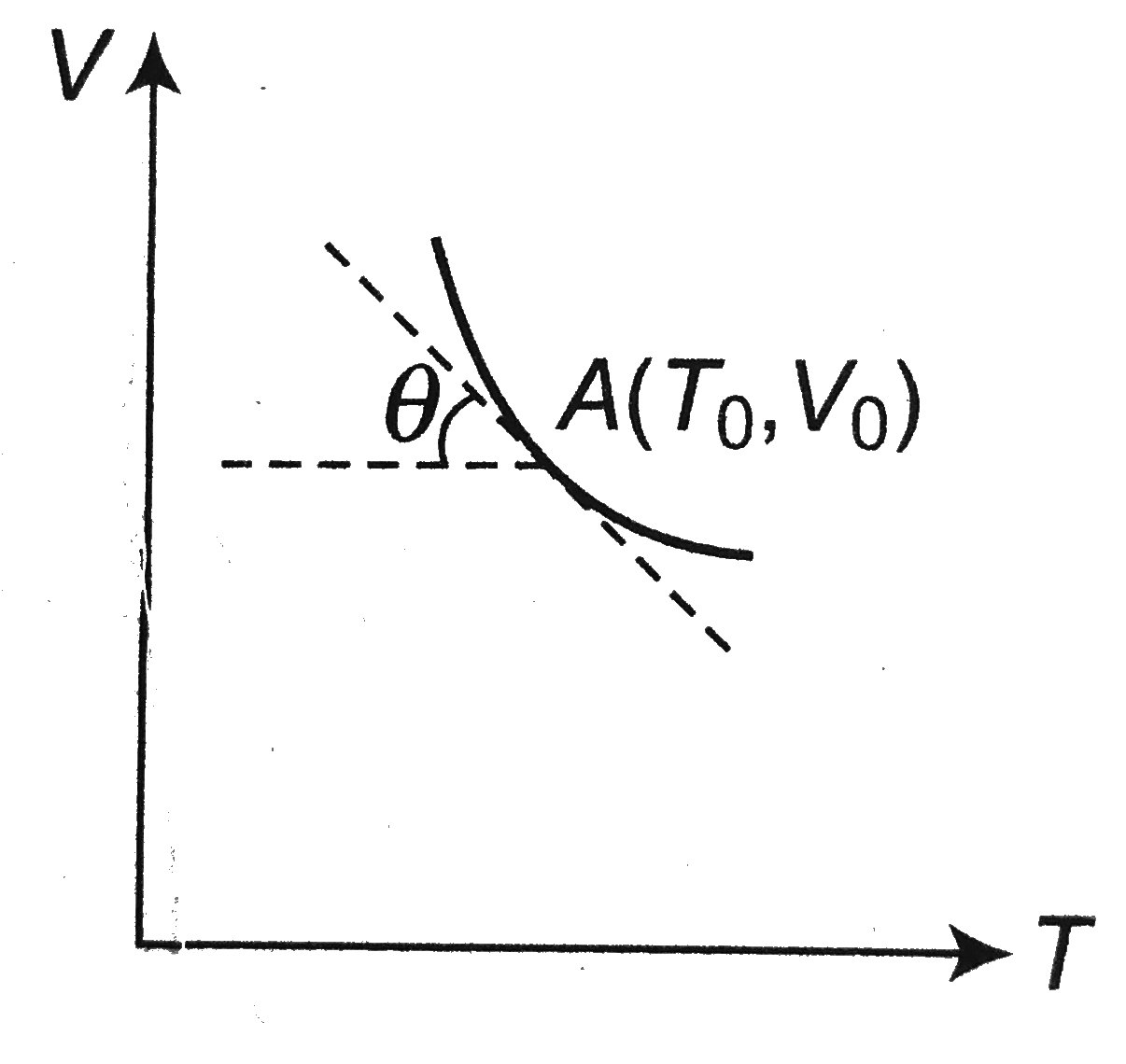A $\frac{V_{0}}{T_{0} tan θ} + 1$
B $\frac{V_{0} tan θ}{T_{0} + 1}$
C $\frac{V_{0} {tan}^{2} θ}{T_{0}} + 1$
D $\frac{V_{0}}{T_{0}} + tan θ$
For an adiabatic change in a gas, if P,V,T denotes pressure, volume and absolute temperature of a gas at any time and $γ$ is the ratio of specific heats of the gas, then which of the following equation is true?
A $T^{γ} P^{1 - γ} =$ const.
B $T^{1 - γ} P^{γ} =$ const.
C $T^{γ - 1} V^{γ} =$ const.
D $T^{γ} V^{γ} =$ const.
If the absolute temperature of a gas is doubled and the pressure is reuced to one-half, the volume of the gas will $____________$
ARemain unchanged
BBe doubled
CIncrease four-fold
DBe reduced to $1 / 4^{t h}$

NTA MOCK TESTS-NTA JEE MOCK TEST 101-PHYSICS

Home
Ask Doubt
Profile