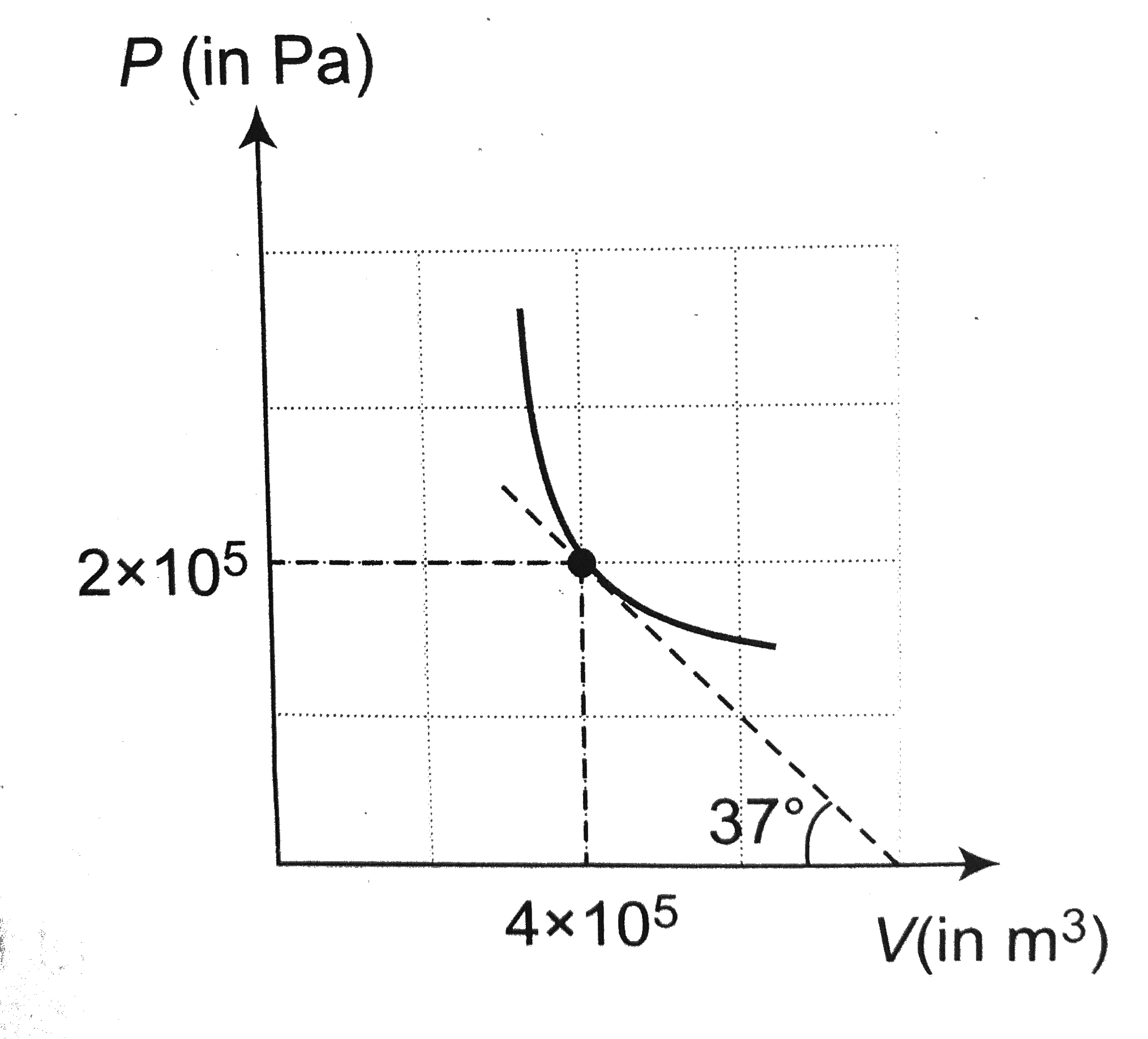
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
34
−32
53
32
The correct Answer is:D
PVm=const.
⇒VmdP+mvm−1Pdv=0
⇒dPdV=−mPV=tan(180−37∘)
=34=m2×1054×105⇒m=32.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Second Law Of Thermodynamics29videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Problems Based On Mixed Concepts49videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - First Law Of Thermodynamics , Internal Energy And Work Done55videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test29videos
GRAVITATION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal monatomic gas undergoes process PV1.25 = constant .Then
Aupon increase in pressure temperature decreasesBupon increase in pressure heat is absorbed by gasCif heat is given to gas its internal energy increasesDheat is absorbed by gas if volume increases - Question 2 - Select One
A certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
A0<n<γB1<n<γCn=γDn>γ - Question 3 - Select One
PV Diagram for ideal gas in piston cylinder assembly undergoing a thermodynamic process is shown in figure. Process is
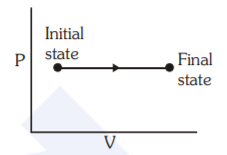 AIsothermalBBasicCIsobaricDAdiabatic
AIsothermalBBasicCIsobaricDAdiabatic
For an ideal gas the ratio of specific heats is CpCv=γ. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View SolutionIn the polytropic process PV2 = constant, is the gas cooled'or heated with increase in volume.
View SolutionAn ideal gas undergoes a polytropic process PV^(n)= constant,such that the molar specific heat during "],[" the process is negative.If the ratio of the specific heats of the gases be Y,then the range of value of n will be
View SolutionFind the molar heat capacity of an ideak gas in a polytropic process pVn=const if the adiabatic exponent of the gas is equal to γ. At what values of the polytropic constant n will the heat capacity of the gas be negative ?
View SolutionOne mole of an ideal gas is taken along the process in which PV'= constant. The graph shown represents the variation of molar heat capacity of such a gas with respect to x. The value of c' and x'c respectively, are given by
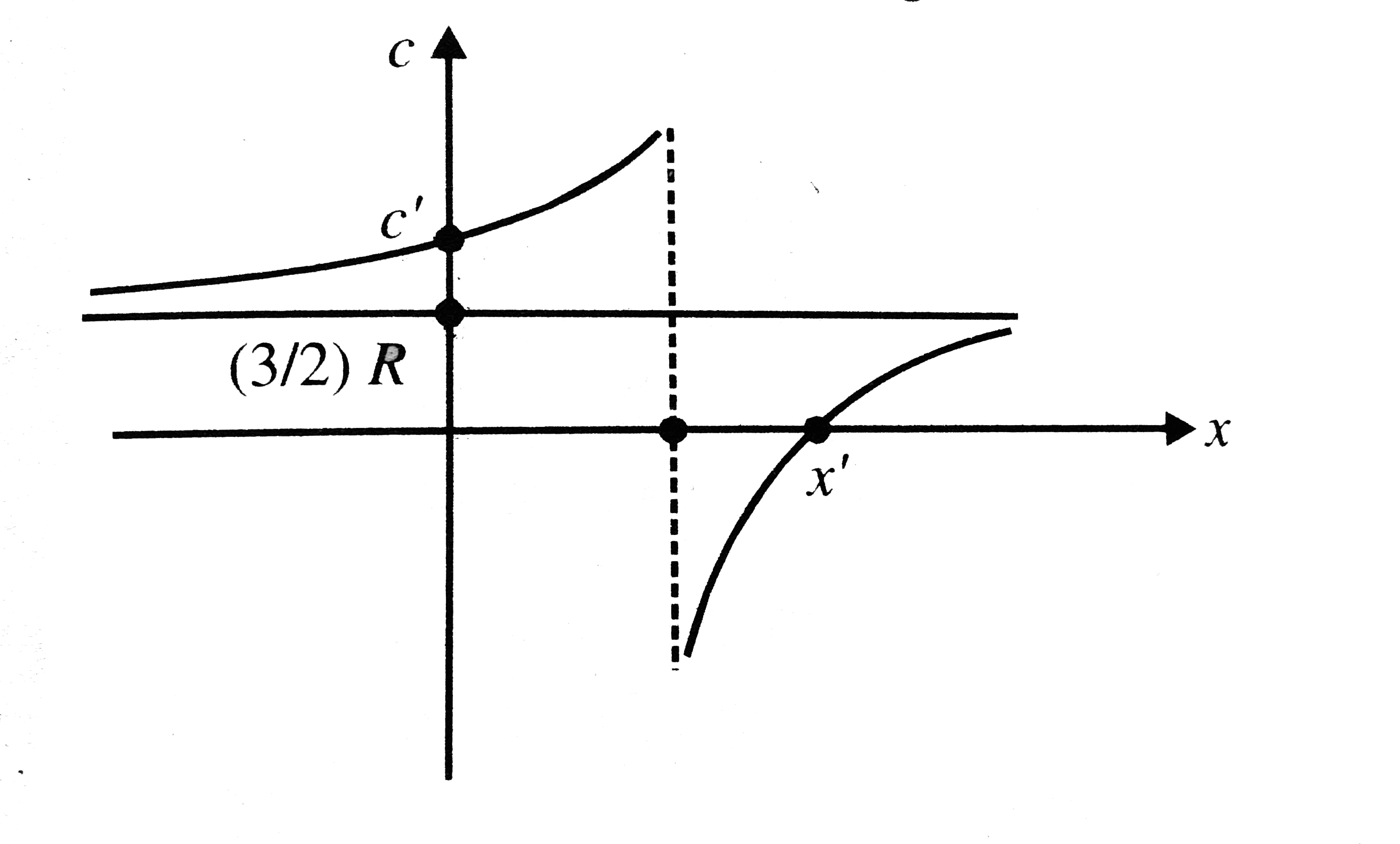 View Solution
View Solution

