For the motion of the mass suspended by a coil spring in example 32.
(i) What is the net force on the suspended mass at its lowermost position ?
(ii) What is the elastic restoring force on the mass due to the spring at its uppermost position ?
Step by step video & image solution for For the motion of the mass suspended by a coil spring in example 32. (i) What is the net force on the suspended mass at its lowermost position ? (ii) What is the elastic restoring force on the mass due to the spring at its uppermost position ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type C Based on Oscillations of a Simple Pendulum
7 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type D Based on Other Examples of SHM
2 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise
233 Videos
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66 Videos
- Physical worldBOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise
49 Videos
Similar Questions
Oscillations of a mass suspended from a vertical spring is ……………………………motion.
View SolutionWhen a body of mass 2.0 kg is suspended by a spring, the spring is stretched. If the body is pulled down slightly and released, it coscillated up and down. What force is applied on the body by the spring when it passes through the mean position ? (g=9.8Nkg−1)
View Solution
Knowledge Check
The restoring force on the body of the above problem due to the spring when it is at its upper most position of its oscillation is
A160 NB40 NC60 ND80 NA simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle θ. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
AkxBmgCmg(cosθ)Dmg(sinθ)A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
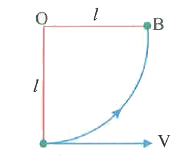 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2gl
The periodic time of a mass suspended by a spring (force constant k) is T. if the spring is cut in three equal pieces, what will be the force constant of each part? If the same mass be suspended from one piece, what will be the periodic time?
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
View SolutionA block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View Solution
