Force constant of a spring (k) is anonymous to
YAL
YLA
ALY
ALY
The correct Answer is:A
To solve the problem regarding the force constant of a spring k, we can follow these steps:
1. Understand the Spring Force Equation:
The force exerted by a spring is given by Hooke's Law:
F=k⋅ΔL
where F is the force applied, k is the spring constant (force constant), and ΔL is the change in length of the spring.
2. Rearranging the Equation for Spring Constant:
From the equation above, we can express the spring constant k as:
k=FΔL
3. Introduce Young's Modulus:
Young's modulus Y is defined as:
Y=F⋅LA⋅ΔL
where L is the original length of the material, A is the cross-sectional area, and ΔL is the change in length.
4. Relate Spring Constant to Young's Modulus:
We can rearrange the equation for Young's modulus to find FΔL:
FΔL=Y⋅AL
5. Substituting into the Spring Constant Equation:
Now, we can substitute this expression into the equation for k:
k=FΔL=Y⋅AL
6. Conclusion:
Therefore, the spring constant k is related to Young's modulus Y, the cross-sectional area A, and the original length L of the spring as:
k=Y⋅AL
Final Answer:
The force constant of a spring k is given by:
k=Y⋅AL
The force exerted by a spring is given by Hooke's Law:
F=k⋅ΔL
where F is the force applied, k is the spring constant (force constant), and ΔL is the change in length of the spring.
From the equation above, we can express the spring constant k as:
k=FΔL
Young's modulus Y is defined as:
Y=F⋅LA⋅ΔL
where L is the original length of the material, A is the cross-sectional area, and ΔL is the change in length.
We can rearrange the equation for Young's modulus to find FΔL:
FΔL=Y⋅AL
Now, we can substitute this expression into the equation for k:
k=FΔL=Y⋅AL
Therefore, the spring constant k is related to Young's modulus Y, the cross-sectional area A, and the original length L of the spring as:
k=Y⋅AL
The force constant of a spring k is given by:
k=Y⋅AL
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
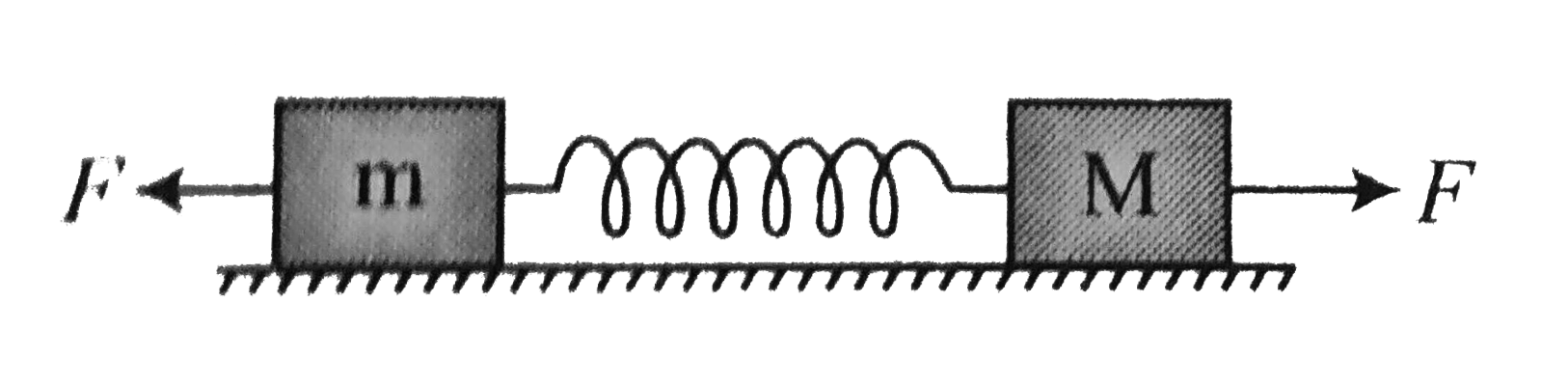
In the situation shown in figure all contact surfaces are smooth. The force constant of the spring is K. Two forces F are applied as shown. The maximum elongation produced in the spring is how many times of F/K (initially the spring is relaxed)?
View SolutionA spring whose instretched length is l has a force constant k. The spring is cut into two pieces of unstretched lengths l1 and l2 where, l1=nl2 and n is an integer. The ratio k1/k2 of the corresponding force constant, k1 and k2 will be :
View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k?
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
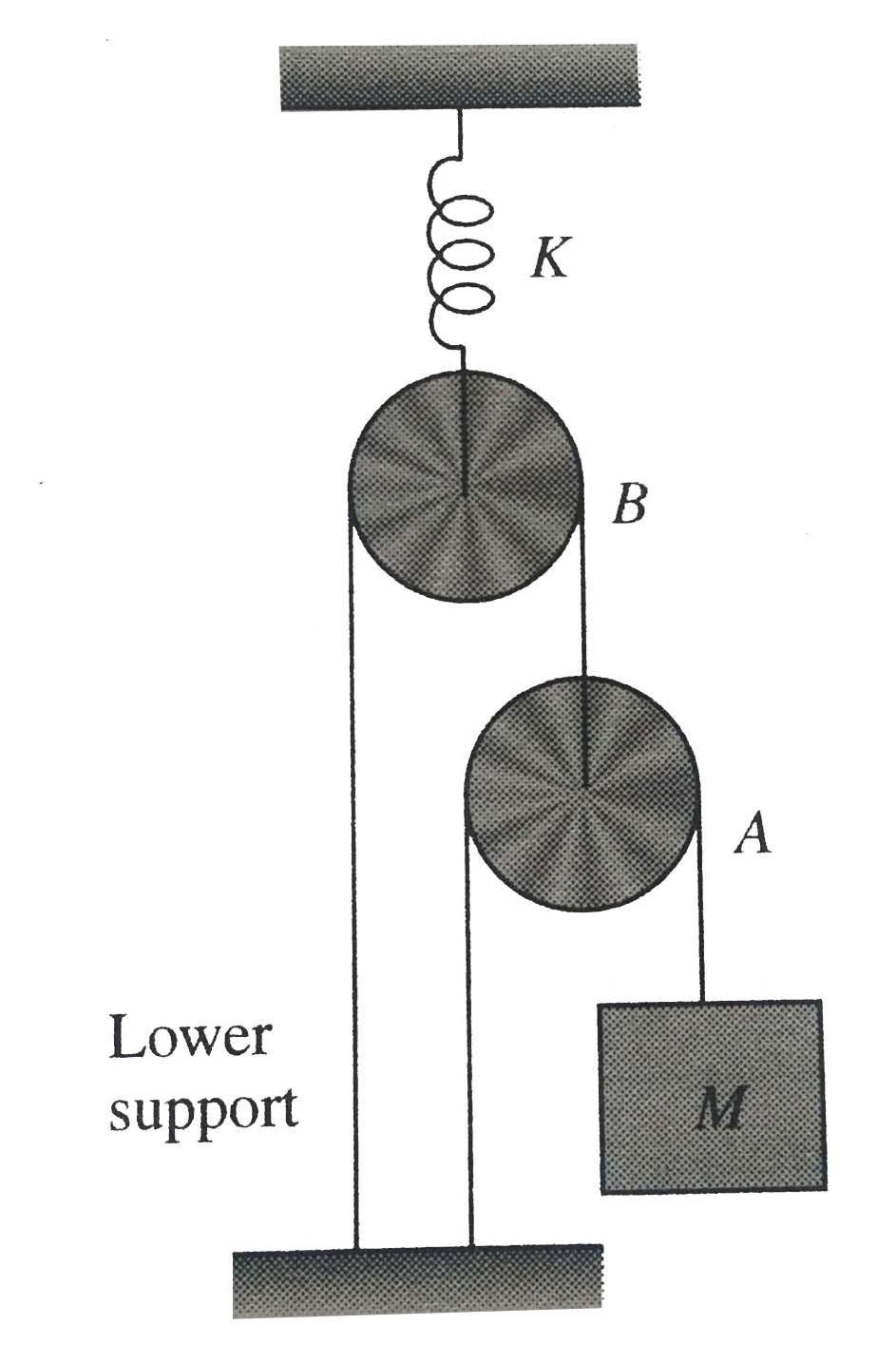
The extension produced in the spring is given by
View SolutionA constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is

View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
View SolutionIn the two block spring system, force constant of spring is k = 6N/m. Spring is stretched by 12 cm and then left. Match the following.

View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

View Solution
