A spring whose instretched length is l has a force constant k. The spring is cut into two pieces of unstretched lengths l1 and l2 where, l1=nl2 and n is an integer. The ratio k1/k2 of the corresponding force constant, k1 and k2 will be :
n
1n2
1n
n2
The correct Answer is:D
To solve the problem, we need to find the ratio of the force constants k1 and k2 of two pieces of a spring that has been cut into two parts. The unstretched lengths of these parts are given as l1 and l2, where l1=nl2.
1. Understanding the Spring Constant:
The spring constant k is related to the unstretched length of the spring. For a spring of unstretched length l and force constant k, the relationship is given by:
k=cl
where c is a constant.
2. Finding the Spring Constants for Each Piece:
For the first piece of the spring with unstretched length l1:
k1=cl1
For the second piece of the spring with unstretched length l2:
k2=cl2
3. Setting Up the Ratio of the Spring Constants:
We want to find the ratio k1k2:
k1k2=cl1cl2=l2l1
Here, the constant c cancels out.
4. Substituting the Relationship Between l1 and l2:
We know from the problem statement that l1=nl2. Substituting this into the ratio gives:
k1k2=l2nl2
5. Simplifying the Expression:
The l2 terms cancel out:
k1k2=1n
6. Conclusion:
Therefore, the ratio of the spring constants k1 and k2 is:
k1k2=1n
Final Answer:
The ratio k1k2 is 1n.
---
The spring constant k is related to the unstretched length of the spring. For a spring of unstretched length l and force constant k, the relationship is given by:
k=cl
where c is a constant.
For the first piece of the spring with unstretched length l1:
k1=cl1
For the second piece of the spring with unstretched length l2:
k2=cl2
We want to find the ratio k1k2:
k1k2=cl1cl2=l2l1
Here, the constant c cancels out.
We know from the problem statement that l1=nl2. Substituting this into the ratio gives:
k1k2=l2nl2
The l2 terms cancel out:
k1k2=1n
Therefore, the ratio of the spring constants k1 and k2 is:
k1k2=1n
The ratio k1k2 is 1n.
Topper's Solved these Questions
Similar Questions
A uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k?
View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k? what is the ratio k1/k2
View SolutionA uniform spring whose unstressed length is l has a force constant k. The spring is cut into two pieces of unstressed lengths l1 and l2 where l1=nl2 where n being on integer. Now a mass m is made to oscillate with first spring. The time period of its oscillation would be
View SolutionForce constant of a spring (k) is anonymous to
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View SolutionA spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
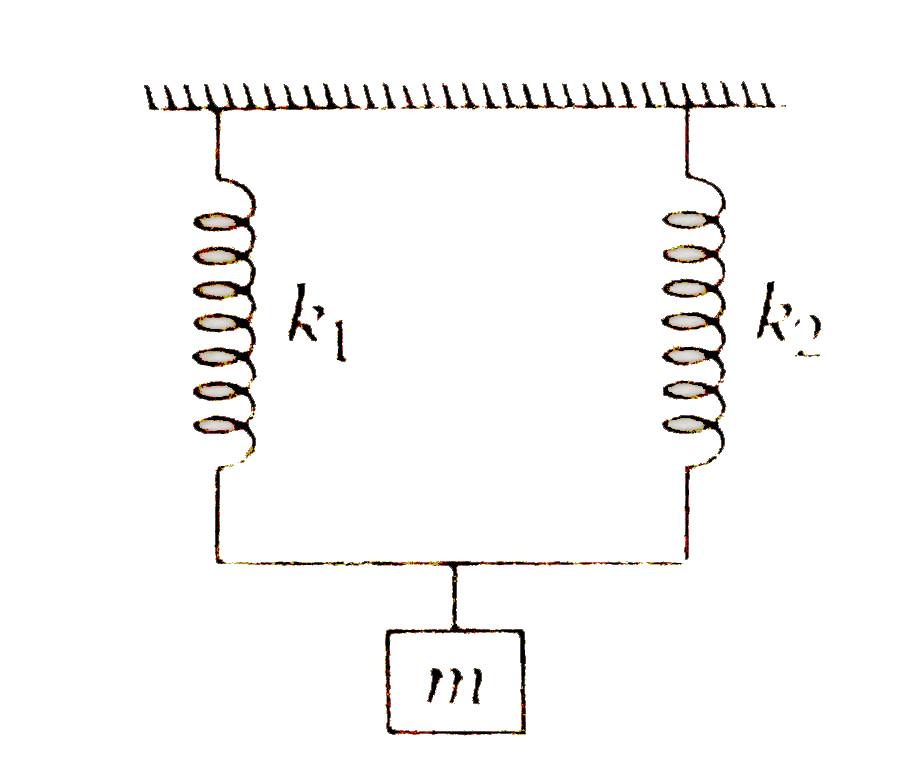
View SolutionThe spring constants of two springs of same length are k1 and k2 as shown in figure. If an object of mass m is suspended and set in vibration , the period will be
View SolutionA block of mass m, when attached to a uniform ideal apring with force constant k and free length L executes SHM. The spring is then cut in two pieces, one with free length n L and other with free length (1−n)L. The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency f1 . The bigger part of the block attached to smaller part of the spring executes SHM with frequency f2. The ratio f1/f2 is
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View Solution
