Comparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
CL
V1CL
CL
LC
The correct Answer is:D
To solve the problem of comparing L-C oscillations with the oscillations of a spring-block system, we can follow these steps:
Step 1: Understand the systems
We have two systems to compare:
1. An L-C circuit (inductor-capacitor circuit) that undergoes oscillations.
2. A spring-block system that oscillates under the influence of a restoring force.
Step 2: Write the equations of motion
For the L-C circuit, we can apply Kirchhoff's law:
E+V=0
Where E is the electromotive force and V is the potential across the capacitor. The equation can be expressed as:
LdIdt+QC=0
Where Q is the charge on the capacitor and I is the current.
Step 3: Substitute for charge
We know that charge Q can be expressed in terms of current:
Q=I⋅t
Substituting this into the equation gives:
LdIdt+I⋅tC=0
Step 4: Differentiate with respect to time
Differentiating the equation with respect to time, we have:
Ld2Idt2+IC=0
Step 5: Compare with the spring-block system
The equation for a spring-block system is given by:
Md2xdt2+Kx=0
Where M is the mass and K is the spring constant.
Step 6: Identify the similarities
From the equations:
- We can see that L (inductance) corresponds to M (mass).
- The term 1C corresponds to K (spring constant).
Thus, we have:
L∼MandK∼1C
Step 7: Calculate the quantity mk
We are asked to find the quantity mk:
mk=M⋅K
Substituting the relationships we found:
mk=L⋅1C=LC
Conclusion
Thus, the physical quantity mk is similar to:
LC
Final Answer
The correct answer is LC.
---
We have two systems to compare:
1. An L-C circuit (inductor-capacitor circuit) that undergoes oscillations.
2. A spring-block system that oscillates under the influence of a restoring force.
For the L-C circuit, we can apply Kirchhoff's law:
E+V=0
Where E is the electromotive force and V is the potential across the capacitor. The equation can be expressed as:
LdIdt+QC=0
Where Q is the charge on the capacitor and I is the current.
We know that charge Q can be expressed in terms of current:
Q=I⋅t
Substituting this into the equation gives:
LdIdt+I⋅tC=0
Differentiating the equation with respect to time, we have:
Ld2Idt2+IC=0
The equation for a spring-block system is given by:
Md2xdt2+Kx=0
Where M is the mass and K is the spring constant.
From the equations:
- We can see that L (inductance) corresponds to M (mass).
- The term 1C corresponds to K (spring constant).
L∼MandK∼1C
We are asked to find the quantity mk:
mk=M⋅K
Substituting the relationships we found:
mk=L⋅1C=LC
Thus, the physical quantity mk is similar to:
LC
The correct answer is LC.
Topper's Solved these Questions
Similar Questions
While comparing the L−C oscillations with the oscillations of spring-block system, with whom the magnetic energy can be compared and why?
View SolutionComparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table Table-1(LC oscillations)Table-2(Spring-block oscillations)(A)L(P)k(B)C(Q)m(C)i(R)v(D)didt(S)x(T)None
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionIn the two block spring system, force constant of spring is k = 6N/m. Spring is stretched by 12 cm and then left. Match the following.

View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
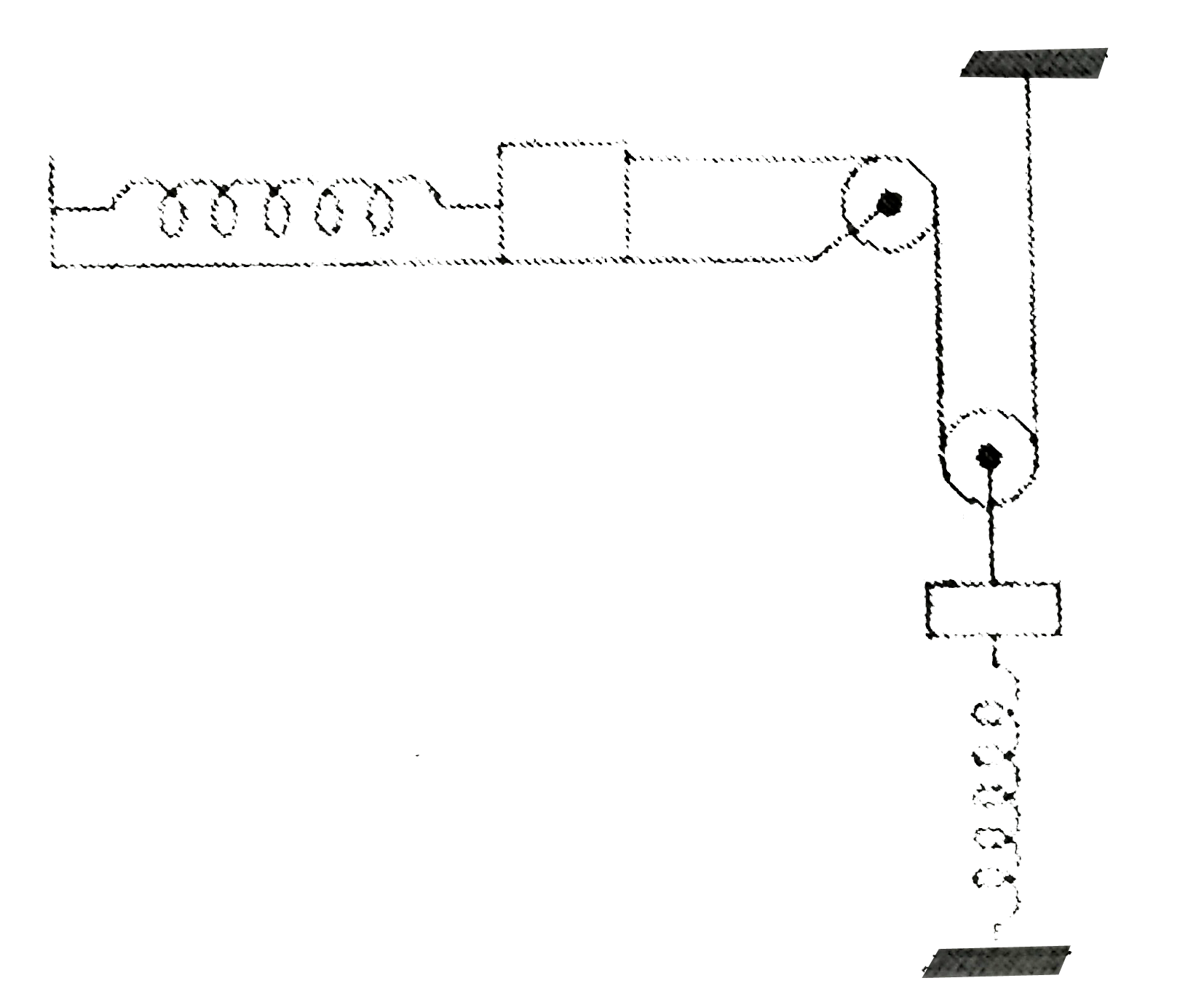
In the equilibrium position, speed of the block placed horizontally is
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionAssertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
View SolutionAssertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
View Solution
