Four charges equal to are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
The correct Answer is:B
To solve the problem of finding the value of charge q at the center of a square with four charges −Q at its corners, we can follow these steps:
Step 1: Understand the Configuration
We have a square with each corner having a charge −Q and a charge q placed at the center. The charges at the corners will exert forces on the charge at the center.
Step 2: Calculate the Distance
The distance from the center of the square to any corner can be calculated using the Pythagorean theorem. If the side length of the square is a, the distance r from the center to a corner is given by:
r=a√2
Step 3: Calculate the Force on Charge q
The force exerted on the charge q at the center by one of the corner charges −Q is given by Coulomb's law:
F=k⋅|q⋅(−Q)|r2
Substituting r=a√2:
F=k⋅|q⋅(−Q)|(a√2)2=2k⋅|q⋅(−Q)|a2
Step 4: Consider the Forces from All Four Charges
Since there are four corner charges, the total force on q due to all four charges will be directed towards the center (attraction), and the magnitude will be:
Ftotal=4⋅2k⋅|q⋅(−Q)|a2=8k⋅|q⋅(−Q)|a2
Step 5: Set the Forces Equal for Equilibrium
For the system to be in equilibrium, the net force acting on charge q must be zero. The force due to the charge q on the charges −Q at the corners must balance the forces exerted by the corner charges. The force exerted by q on one of the corner charges −Q is:
Fq=k⋅|q⋅(−Q)|(a√2)2=2k⋅|q⋅(−Q)|a2
Step 6: Balance the Forces
Setting the total force due to the corner charges equal to the force due to charge q:
8k⋅|q⋅(−Q)|a2=2k⋅|q⋅(−Q)|a2
Step 7: Solve for q
Since k, |Q|, and a2 are common factors, we can simplify:
8|q|=2|q|⟹8=2⟹|q|=0
However, this indicates that the charge q must be positive to balance the negative charges at the corners. Thus, we find:
q=Q4(1+2√2)
Final Answer
The value of charge q at the center for the system to be in equilibrium is:
q=Q4(1+2√2)
We have a square with each corner having a charge −Q and a charge q placed at the center. The charges at the corners will exert forces on the charge at the center.
The distance from the center of the square to any corner can be calculated using the Pythagorean theorem. If the side length of the square is a, the distance r from the center to a corner is given by:
r=a√2
The force exerted on the charge q at the center by one of the corner charges −Q is given by Coulomb's law:
F=k⋅|q⋅(−Q)|r2
Substituting r=a√2:
F=k⋅|q⋅(−Q)|(a√2)2=2k⋅|q⋅(−Q)|a2
Since there are four corner charges, the total force on q due to all four charges will be directed towards the center (attraction), and the magnitude will be:
Ftotal=4⋅2k⋅|q⋅(−Q)|a2=8k⋅|q⋅(−Q)|a2
For the system to be in equilibrium, the net force acting on charge q must be zero. The force due to the charge q on the charges −Q at the corners must balance the forces exerted by the corner charges. The force exerted by q on one of the corner charges −Q is:
Fq=k⋅|q⋅(−Q)|(a√2)2=2k⋅|q⋅(−Q)|a2
Setting the total force due to the corner charges equal to the force due to charge q:
8k⋅|q⋅(−Q)|a2=2k⋅|q⋅(−Q)|a2
Since k, |Q|, and a2 are common factors, we can simplify:
8|q|=2|q|⟹8=2⟹|q|=0
q=Q4(1+2√2)
The value of charge q at the center for the system to be in equilibrium is:
q=Q4(1+2√2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answer Type1videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type22videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension Type2videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
Four point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
 View Solution
View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View Solution
Knowledge Check
- Question 1 - Select One
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Four identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .View Solution
.View SolutionFour charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the souare will be (where k = 14πε0 )
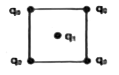
View SolutionFour equal charges are kept fixed on the vertices of a square of side 'a'. A charge q1 is kept at the centre of the square as shown in the figure . Then
 View Solution
View Solution

