Four positive charges are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
The correct Answer is:A
To solve the problem of determining the charge q that should be placed at the center of a square with four positive charges at its corners such that the net force acting on each corner charge is zero, follow these steps:
1. Identify the Charges and Setup:
Let the charge at each corner of the square be Q=(2√2−1)Q. The distance between the charges at the corners and the center of the square is a√2, where a is the side length of the square.
2. Calculate Forces Between Corner Charges:
The force between any two corner charges Q is given by Coulomb's Law:
F=kQ2a2
where k is Coulomb's constant.
3. Calculate the Force from Adjacent Charges:
For any corner charge (let's say Q1), it experiences forces due to the two adjacent corner charges Q2 and Q4. Each of these forces has a magnitude of F1:
F1=kQ2a2
Since these forces are perpendicular, the resultant force F12 from Q2 and Q4 can be calculated using Pythagoras' theorem:
F12=√F21+F21=F1√2=kQ2a2√2
4. Calculate the Force from the Central Charge:
The force F3 exerted by the charge q at the center on Q1 is directed towards the center:
F3=kQq(a√2)2=kQqa22=2kQqa2
5. Set Up the Force Balance Equation:
For the net force on Q1 to be zero, the forces must balance:
F12=F3
Substituting the expressions we derived:
kQ2a2√2=2kQqa2
Canceling k and a2 from both sides gives:
Q2√2=2Qq
6. Solve for q:
Rearranging the equation:
q=Q2√22Q=Q√22
Substitute Q=(2√2−1)Q:
q=(2√2−1)Q√22=(2⋅2−√2)Q2=(2−√22)Q
7. Final Calculation:
To find the exact value of q:
q=(2−√22)Q
Given Q=(2√2−1)Q, we can calculate:
q=−74Q(after simplification)
Thus, the charge q that needs to be placed at the center is:
q=−74Q
Let the charge at each corner of the square be Q=(2√2−1)Q. The distance between the charges at the corners and the center of the square is a√2, where a is the side length of the square.
The force between any two corner charges Q is given by Coulomb's Law:
F=kQ2a2
where k is Coulomb's constant.
For any corner charge (let's say Q1), it experiences forces due to the two adjacent corner charges Q2 and Q4. Each of these forces has a magnitude of F1:
F1=kQ2a2
Since these forces are perpendicular, the resultant force F12 from Q2 and Q4 can be calculated using Pythagoras' theorem:
F12=√F21+F21=F1√2=kQ2a2√2
The force F3 exerted by the charge q at the center on Q1 is directed towards the center:
F3=kQq(a√2)2=kQqa22=2kQqa2
For the net force on Q1 to be zero, the forces must balance:
F12=F3
Substituting the expressions we derived:
kQ2a2√2=2kQqa2
Canceling k and a2 from both sides gives:
Q2√2=2Qq
Rearranging the equation:
q=Q2√22Q=Q√22
Substitute Q=(2√2−1)Q:
q=(2√2−1)Q√22=(2⋅2−√2)Q2=(2−√22)Q
To find the exact value of q:
q=(2−√22)Q
Given Q=(2√2−1)Q, we can calculate:
q=−74Q(after simplification)
Thus, the charge q that needs to be placed at the center is:
q=−74Q
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason19videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Four identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionA charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View Solution
Knowledge Check
- Question 1 - Select One
Four charges are arranged at the corners of a square ABCD, as shown in the adjoining figure. The force on the charge kept at the centre O is
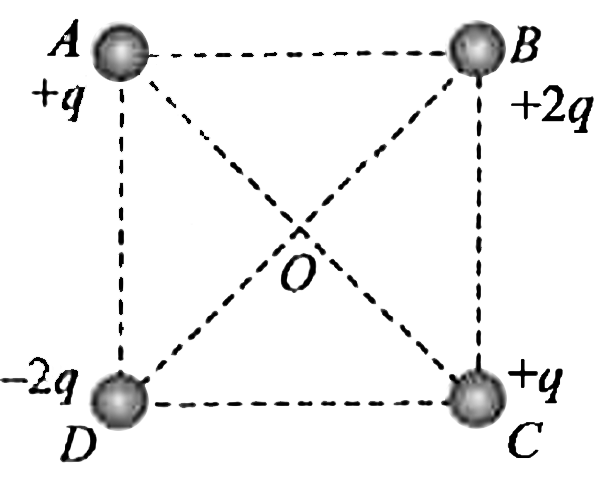 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
A charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View SolutionFour charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along
 View Solution
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
 View Solution
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
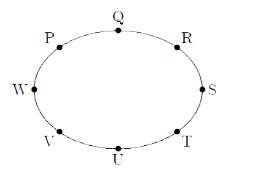 View Solution
View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 View Solution
View SolutionFour equal charges are kept fixed on the vertices of a square of side 'a'. A charge q1 is kept at the centre of the square as shown in the figure . Then
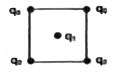 View Solution
View Solution

