Four equal charges each are fixed at the four corners of a squae of side 5 cm. Find the coulomba force eperienced by one of the charges due to the rest three.
To solve the problem of finding the Coulomb force experienced by one of the charges due to the other three charges located at the corners of a square, we will follow these steps:
Step 1: Understand the Configuration
We have four equal charges Q=2.0×10−6C fixed at the corners of a square with a side length of a=5cm=0.05m.
Step 2: Calculate the Forces Due to Each Charge
1. Force due to the charge directly adjacent (F1):
The force between two charges is given by Coulomb's law:
F=kQ2r2
For the charges at adjacent corners, the distance r=a:
F1=kQ2a2
2. Force due to the charge diagonally opposite (F2):
The distance between the charges at opposite corners is given by the diagonal of the square:
r=√2a
Therefore, the force F2 is:
F2=kQ2(√2a)2=kQ22a2
Step 3: Substitute Values
Using k=8.99×109N m2/C2:
1. Calculate F1:
F1=8.99×109(2.0×10−6)2(0.05)2=8.99×1094.0×10−120.0025=14.384N
2. Calculate F2:
F2=8.99×109(2.0×10−6)22(0.05)2=8.99×1094.0×10−120.005=7.192N
Step 4: Determine the Resultant Force
1. The forces F1 and F2 act at right angles to each other. The resultant force FR can be calculated using the Pythagorean theorem:
FR=√F21+F22
Substituting the values:
FR=√(14.384)2+(7.192)2=√206.5+51.8=√258.3≈16.1N
Step 5: Conclusion
The total Coulomb force experienced by one of the charges due to the other three charges is approximately 16.1N.
---
We have four equal charges Q=2.0×10−6C fixed at the corners of a square with a side length of a=5cm=0.05m.
1. Force due to the charge directly adjacent (F1):
The force between two charges is given by Coulomb's law:
F=kQ2r2
For the charges at adjacent corners, the distance r=a:
F1=kQ2a2
The distance between the charges at opposite corners is given by the diagonal of the square:
r=√2a
Therefore, the force F2 is:
F2=kQ2(√2a)2=kQ22a2
Using k=8.99×109N m2/C2:
1. Calculate F1:
F1=8.99×109(2.0×10−6)2(0.05)2=8.99×1094.0×10−120.0025=14.384N
F2=8.99×109(2.0×10−6)22(0.05)2=8.99×1094.0×10−120.005=7.192N
1. The forces F1 and F2 act at right angles to each other. The resultant force FR can be calculated using the Pythagorean theorem:
FR=√F21+F22
Substituting the values:
FR=√(14.384)2+(7.192)2=√206.5+51.8=√258.3≈16.1N
The total Coulomb force experienced by one of the charges due to the other three charges is approximately 16.1N.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Three equal charges, 2.0×10−6 C each, are held fixed at the three corners of a square of side 5 cm. find the Coulomb force experienced by one of the charges due to the rest two.
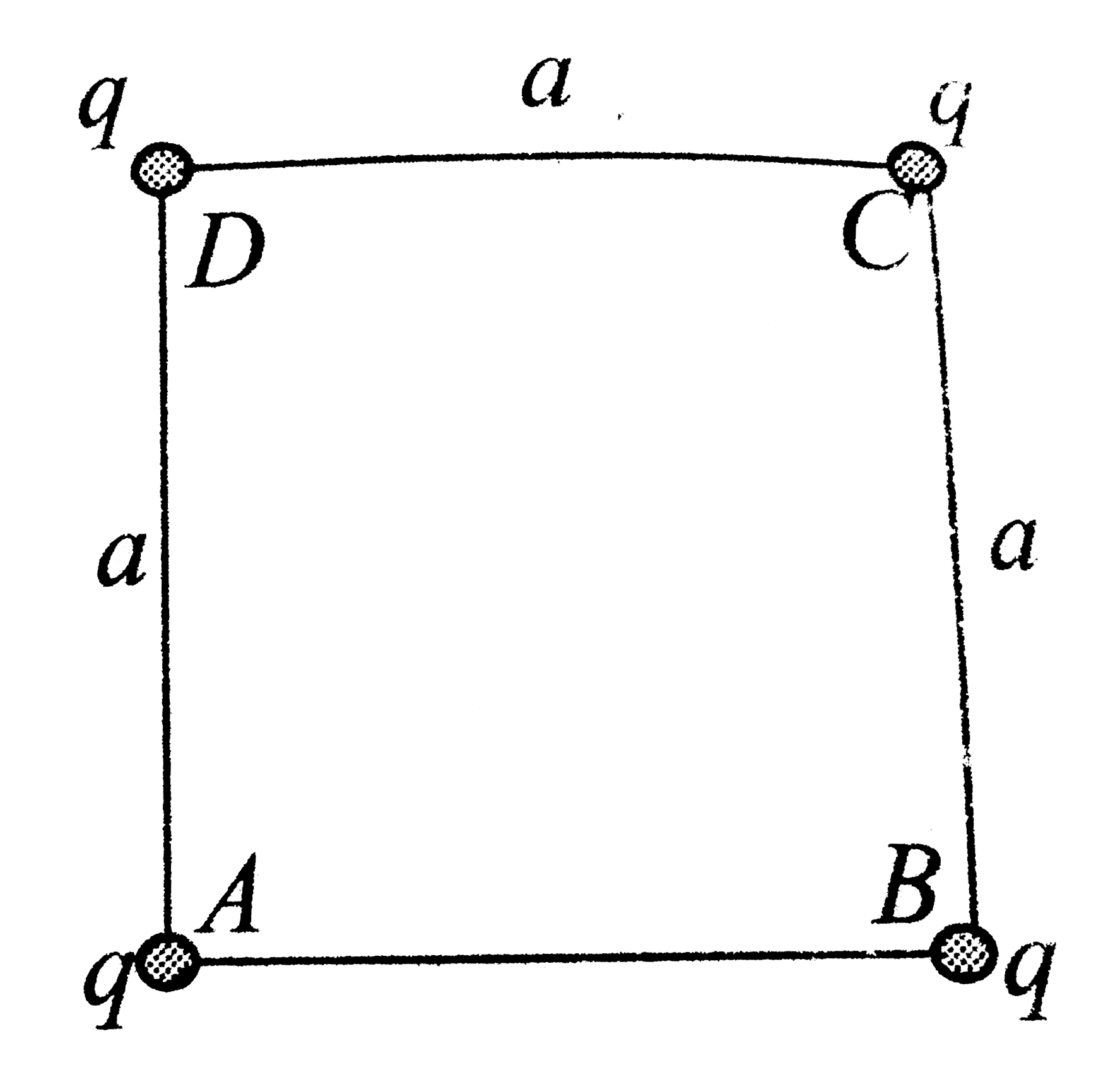
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
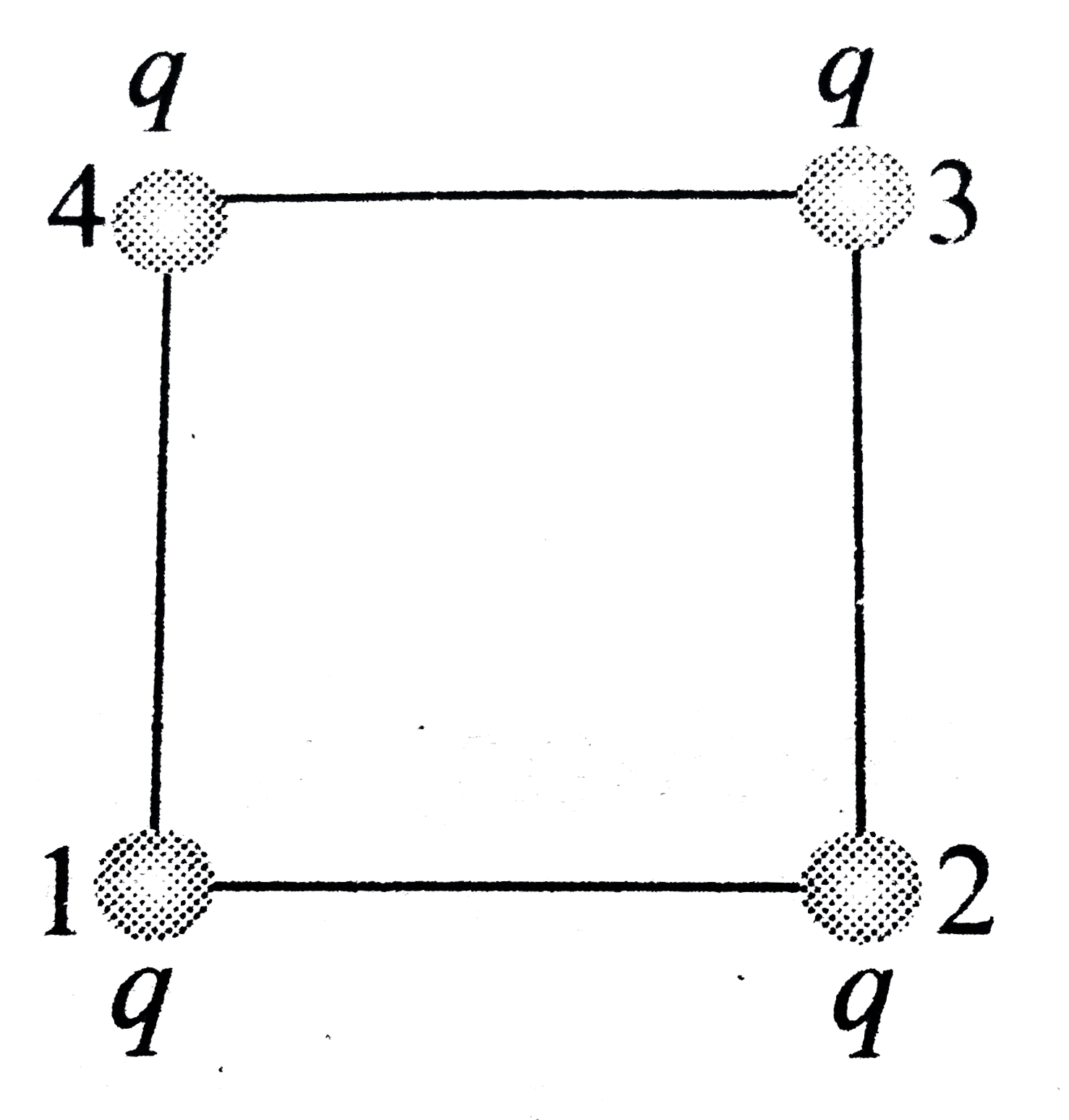
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionCharges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
View SolutionCharges 5.0×10−7C,−2.5×10−7Cand1.0×10−7C are
held fixed at the three corners A, B, C of equilateral triangle of side 10cm respectively. Find the electric force on the charge at C due to the rest two.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree equal charges, each having a magnitude of. 2.0×10−6C, are placed at the thre corners of a right. angled triangle of sides 3 cm, 4cm and 5 cm. find the force (in magnitude) on the charge at the right angled
View Solution
