Two identically charged particles are fastened to the two ends of a spring of spring constant 100Nm−1, find the extension In the length of the spring. Assume that the extension is small as compared to the natural length . Justify this assumption after you solve the problem.
To solve the problem of finding the extension in the length of the spring when two identically charged particles are fastened to its ends, we can follow these steps:
1. Identify the Forces Acting on the Spring:
The two charged particles will exert an electrostatic repulsive force on each other due to their identical charges. This force will cause the spring to extend.
2. Use Coulomb's Law for Electrostatic Force:
The electrostatic force Fe between two point charges Q separated by a distance r is given by Coulomb's law:
Fe=keQ2r2
where ke is the electrostatic constant (approximately 9×109N m2/C2).
3. Consider the Natural Length of the Spring:
Let the natural (unstretched) length of the spring be R. When the spring is extended by X, the new length becomes R+X.
4. Set Up the Equation for Forces:
At equilibrium, the electrostatic force will be equal to the restoring force of the spring. The restoring force Fs of the spring is given by Hooke's law:
Fs=ksX
where ks is the spring constant (given as 100N/m).
5. Equate the Forces:
Setting the electrostatic force equal to the spring force gives:
keQ2(R+X)2=ksX
6. Assume Small Extension:
Since we assume that the extension X is small compared to the natural length R, we can approximate (R+X)2 as R2:
keQ2R2=ksX
7. Solve for Extension X:
Rearranging the equation to solve for X:
X=keQ2ksR2
8. Substitute Known Values:
Substitute ke=9×109N m2/C2, ks=100N/m, and R (the natural length) into the equation:
X=9×109Q2100R2
Conclusion:
The extension X in the length of the spring is given by:
X=9×109Q2100R2
Justification for the Assumption:
The assumption that the extension X is small compared to the natural length R allows us to simplify the expression (R+X)2 to R2. This approximation is valid when X is much smaller than R, ensuring that the spring behaves linearly according to Hooke's law.
The two charged particles will exert an electrostatic repulsive force on each other due to their identical charges. This force will cause the spring to extend.
The electrostatic force Fe between two point charges Q separated by a distance r is given by Coulomb's law:
Fe=keQ2r2
where ke is the electrostatic constant (approximately 9×109N m2/C2).
Let the natural (unstretched) length of the spring be R. When the spring is extended by X, the new length becomes R+X.
At equilibrium, the electrostatic force will be equal to the restoring force of the spring. The restoring force Fs of the spring is given by Hooke's law:
Fs=ksX
where ks is the spring constant (given as 100N/m).
Setting the electrostatic force equal to the spring force gives:
keQ2(R+X)2=ksX
Since we assume that the extension X is small compared to the natural length R, we can approximate (R+X)2 as R2:
keQ2R2=ksX
Rearranging the equation to solve for X:
X=keQ2ksR2
Substitute ke=9×109N m2/C2, ks=100N/m, and R (the natural length) into the equation:
X=9×109Q2100R2
The extension X in the length of the spring is given by:
X=9×109Q2100R2
The assumption that the extension X is small compared to the natural length R allows us to simplify the expression (R+X)2 to R2. This approximation is valid when X is much smaller than R, ensuring that the spring behaves linearly according to Hooke's law.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer14videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 19videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples19videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two springs of spring constants 1000Nm−1 and 2000Nm−1 are stretched with same force. They will have potential energy in the ratio of
A2:1B22:12C1:2D12:22 - Question 2 - Select One
Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cm
Two equal masses are attached to the two end of a spring of force constant k the masses are pulled out symmetrically to stretch the spring by a length 2x0 over its natural length. Find the work done by the spring on each mass.
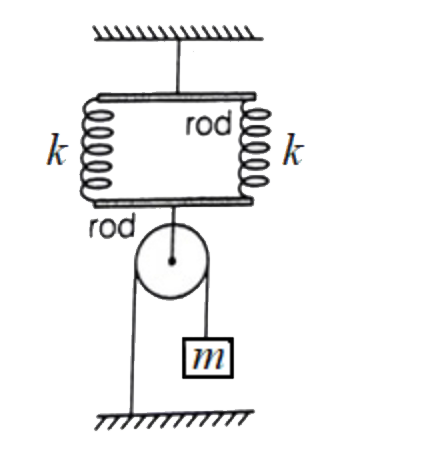
View SolutionThere are two identical spring each of spring constant k. here springs, pulley and rods are massless and the block has mass m . What is the extension of each spring at equilibrium?
 View Solution
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :
 View Solution
View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.
 View Solution
View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View Solution

