Four identical point masses m each are kept at the vertices A, B, and C of a cube having side length ‘a’ (see figure). Another identical mass is placed at the center point D of the cube. (a) Where will you place a fifth identical mass so that the net gravitational force acting on mass at D becomes zero? (b) Calculate the net gravitational force acting on the mass at D.

The correct Answer is:At the diagonally opposite corner of C on the floor of the cube
Step by step video, text & image solution for Four identical point masses m each are kept at the vertices A, B, and C of a cube having side length ‘a’ (see figure). Another identical mass is placed at the center point D of the cube. (a) Where will you place a fifth identical mass so that the net gravitational force acting on mass at D becomes zero? (b) Calculate the net gravitational force acting on the mass at D. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View Solution
Knowledge Check
If the net external force acting on a system is zero, then the centre of mass?
Amust not moveBmust not accelerateCmay moveDmay accelerateThree masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Four identical masses m each are kept at points A, B, C & D shown in figure. Gravitational force on mass at point D (body centre) is -
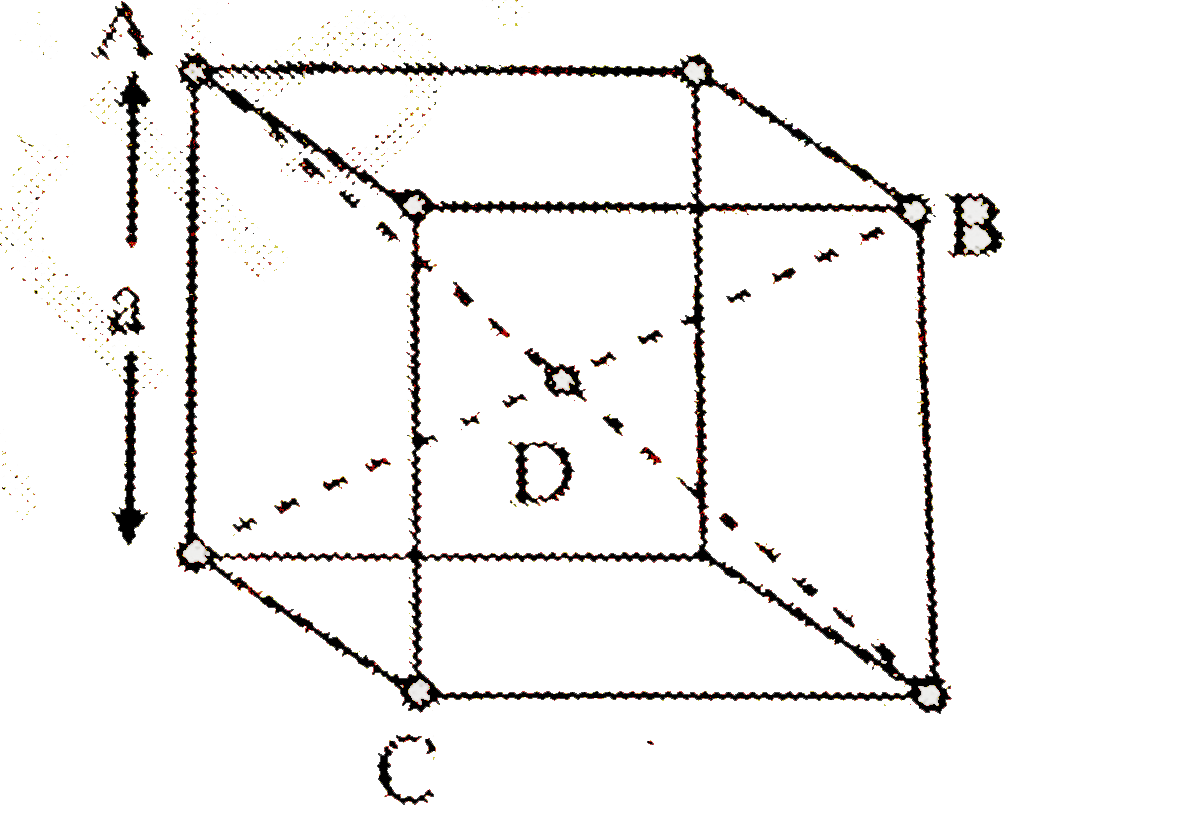 A3Gm2a2B12Gm2a2C4Gm2a2D4Gm23a2
A3Gm2a2B12Gm2a2C4Gm2a2D4Gm23a2
A small point mass m is placed at the centre of curvature of acircular are of radius R and mass 3 m as shown in figure−6.31.Find the net gravitational force acting on the point mass.

View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
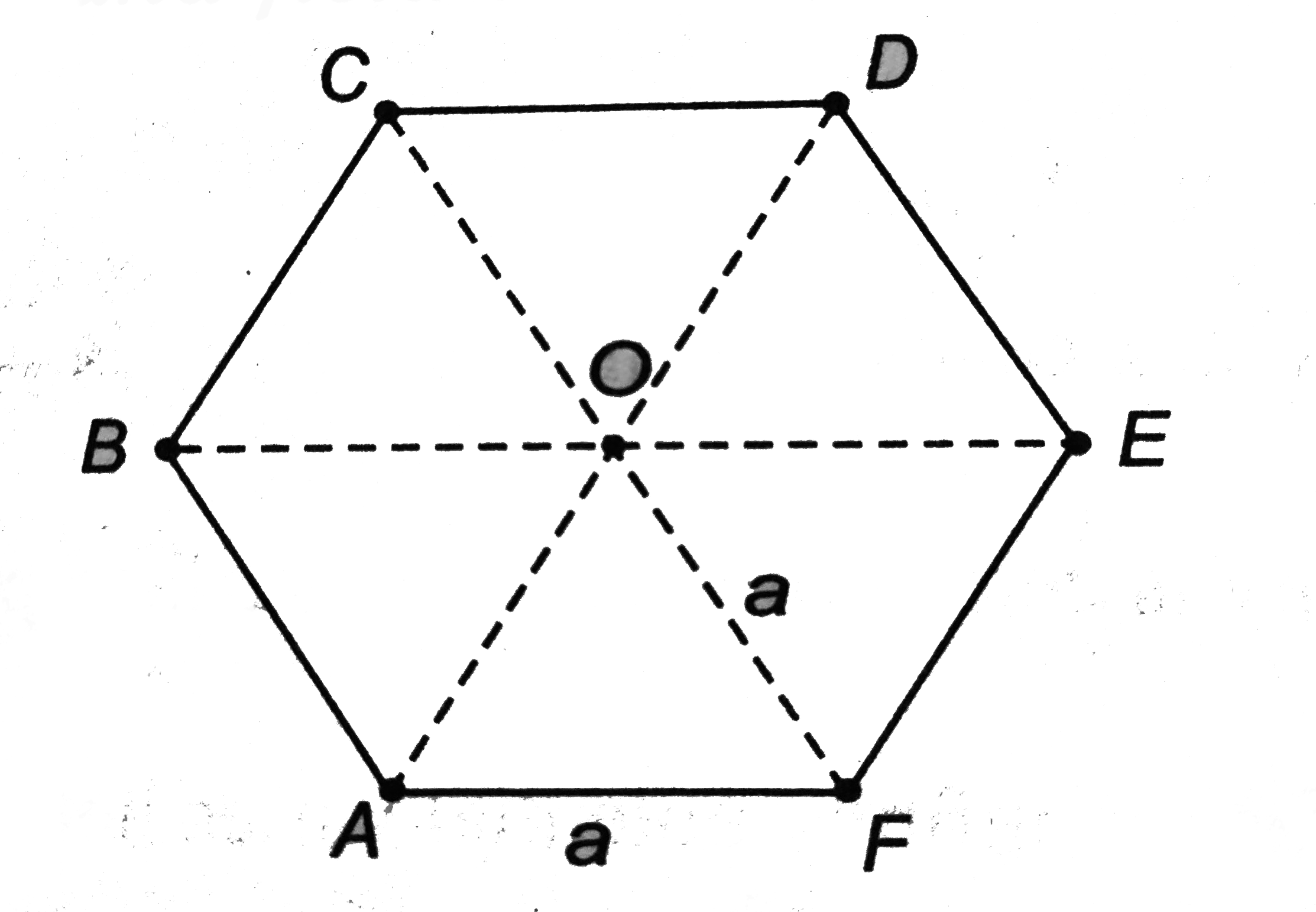 .
.
View SolutionA mass is at the center of a square, with four masses at the corners as shown.
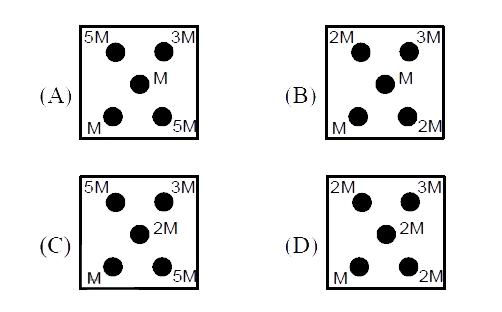
Rank the choices according to the magnitude of the gravitational force on the center mass.
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
View Solution
