A mass is at the center of a square, with four masses at the corners as shown.
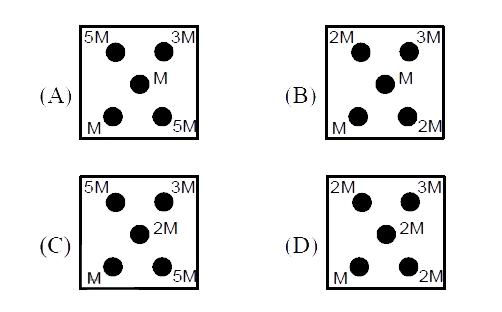
Rank the choices according to the magnitude of the gravitational force on the center mass.
FA=FB<FC=FD
FA>FB<FD<FC
FA=FB>FC=FD
none
The correct Answer is:A
Step by step video & image solution for A mass is at the center of a square, with four masses at the corners as shown. Rank the choices according to the magnitude of the gravitational force on the center mass. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 2 (Level - II) Multiple choice | JEE Advanced
12 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 3 | level - 1 (Subjective | JEE Advanced)
13 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 1 (Objective Problems | Jee Main
25 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22 Videos
Similar Questions
Knowledge Check
A mass is at the centre of a square, with four masses at corners as shown
Rank the choice according to the magnitude of the gravitational force of the centre mass


Rank the choice according to the magnitude of the gravitational force of the centre mass-AFA=FB<FC=FDBFA>FB<FD<FCCFA=FB>FC=FDDnoneThe figure shows four arrangement of three particles of equal masses. Rank the arrangement according to the magnitude of the net gravitational force on the particle m, greatest first.
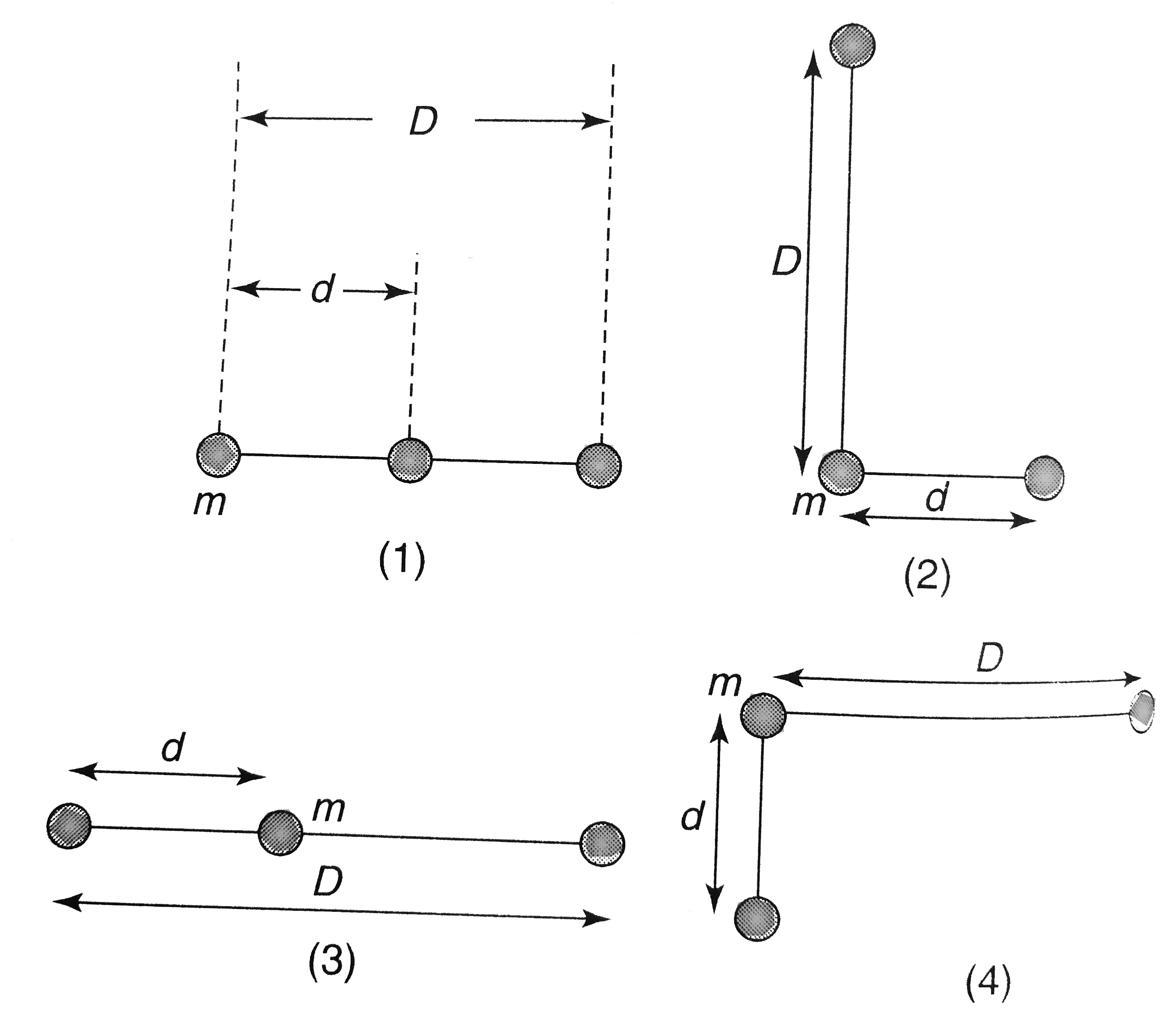 A1, tie of 2 and 4, then 3B1,4,3,2C2,3,4,1D4,3,1,2
A1, tie of 2 and 4, then 3B1,4,3,2C2,3,4,1D4,3,1,2Two particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
AzeroB7Gm4r2C9Gm4r2D3Gm2r2
A particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them

View SolutionFind the center of mass of the four point masses as shown in figure.
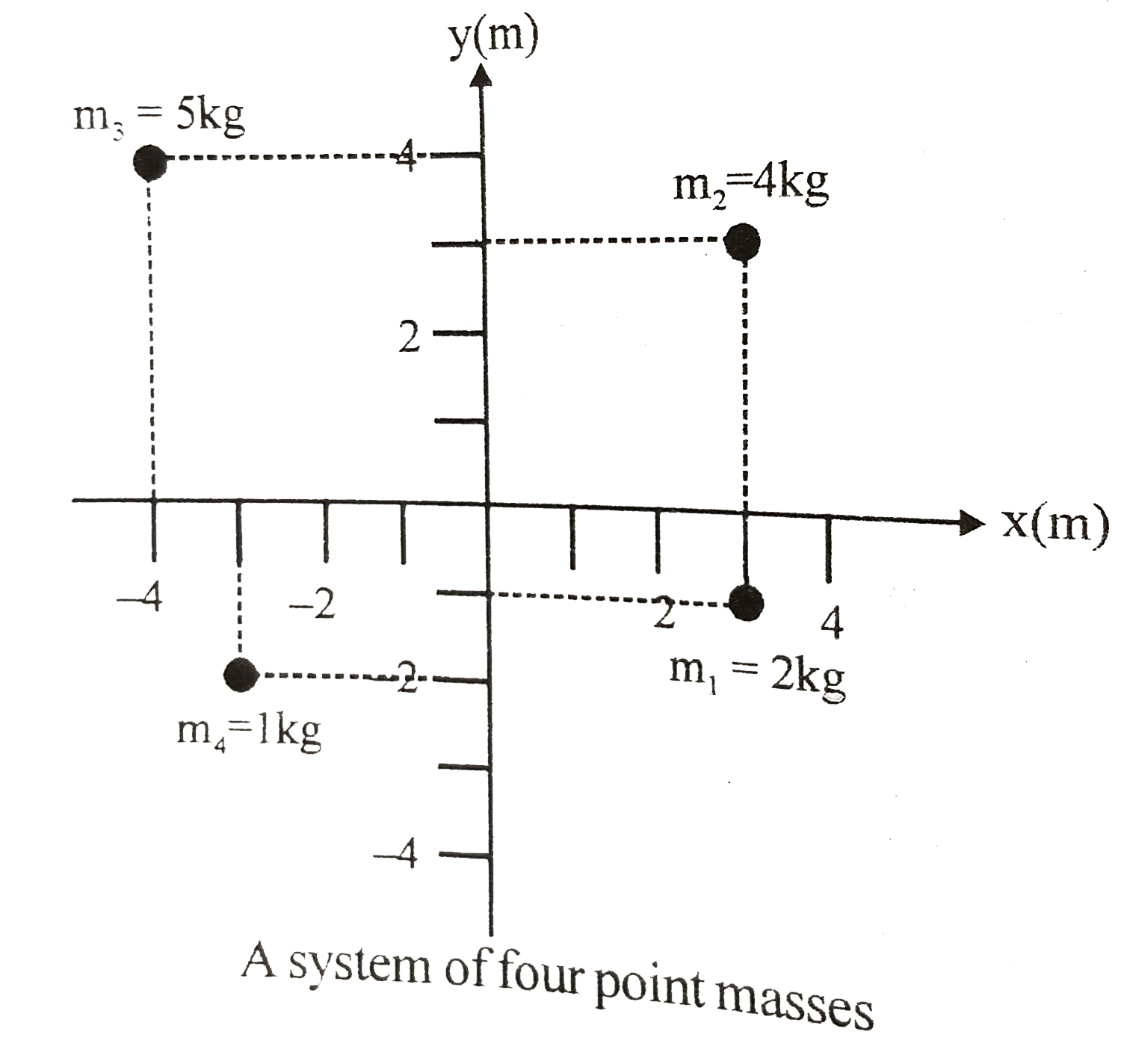
View SolutionCenter of Mass Questions
View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View SolutionThree particles, two with mass m and one with mass M, might be arranged in any of Rank the configuration according of the gravitational force on M, least to greatest.

View Solution

