Four particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is 'a'. Find the electric field at the centre of pentagon.
The correct Answer is:A, B, D
To find the electric field at the center of a regular pentagon with four charges q placed at its vertices, we can follow these steps:
Step 1: Understand the Configuration
We have a regular pentagon with four charges q located at four of its vertices. The distance from the center of the pentagon to each vertex is a.
Step 2: Calculate the Electric Field Due to One Charge
The electric field E due to a point charge q at a distance r is given by the formula:
E=k⋅qr2
where k is Coulomb's constant. Since the distance from the center to each vertex is a, the electric field due to one charge at the center will be:
E=k⋅qa2
Step 3: Determine the Direction of the Electric Fields
The electric field vectors due to each charge will point away from the charge if the charge is positive. Since all four charges are equal and positive, the electric fields will point outward from each charge toward the center.
Step 4: Analyze the Symmetry
Due to the symmetry of the pentagon, the electric fields produced by the charges at the vertices will have components that cancel each other out. Specifically, for every charge, there is another charge opposite to it that will produce an electric field in the opposite direction.
Step 5: Calculate the Net Electric Field
Since the charges are symmetrically placed, the horizontal components of the electric fields will cancel out, and the vertical components will also cancel out. Therefore, the net electric field at the center of the pentagon due to the four charges will be:
Enet=0
Conclusion
The electric field at the center of the pentagon, due to the four charges placed at its vertices, is zero.
We have a regular pentagon with four charges q located at four of its vertices. The distance from the center of the pentagon to each vertex is a.
The electric field E due to a point charge q at a distance r is given by the formula:
E=k⋅qr2
where k is Coulomb's constant. Since the distance from the center to each vertex is a, the electric field due to one charge at the center will be:
E=k⋅qa2
The electric field vectors due to each charge will point away from the charge if the charge is positive. Since all four charges are equal and positive, the electric fields will point outward from each charge toward the center.
Due to the symmetry of the pentagon, the electric fields produced by the charges at the vertices will have components that cancel each other out. Specifically, for every charge, there is another charge opposite to it that will produce an electric field in the opposite direction.
Since the charges are symmetrically placed, the horizontal components of the electric fields will cancel out, and the vertical components will also cancel out. Therefore, the net electric field at the center of the pentagon due to the four charges will be:
Enet=0
The electric field at the center of the pentagon, due to the four charges placed at its vertices, is zero.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.5
3 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.6
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.3
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
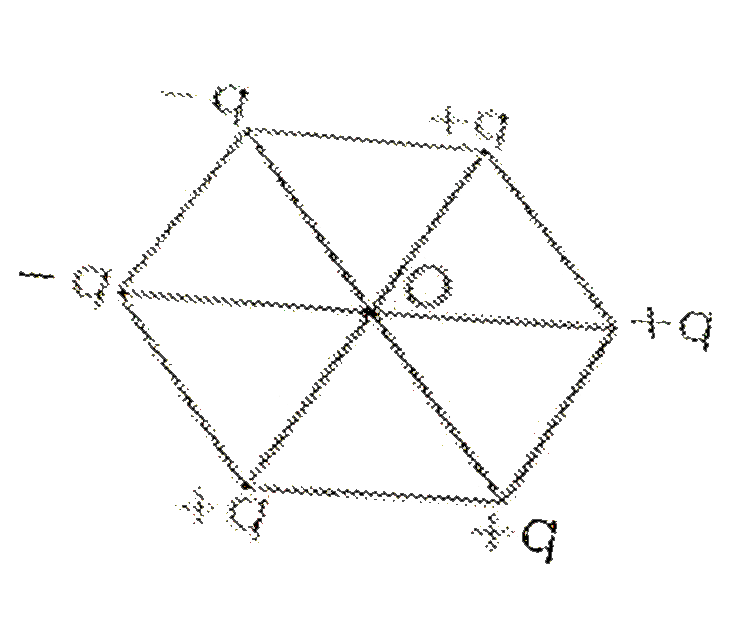
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
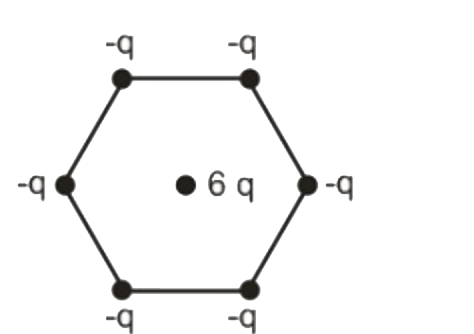
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionProve that the any four vertices of a regular pentagon are concyclic (lie on the same circle).
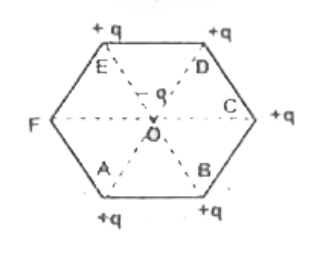
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
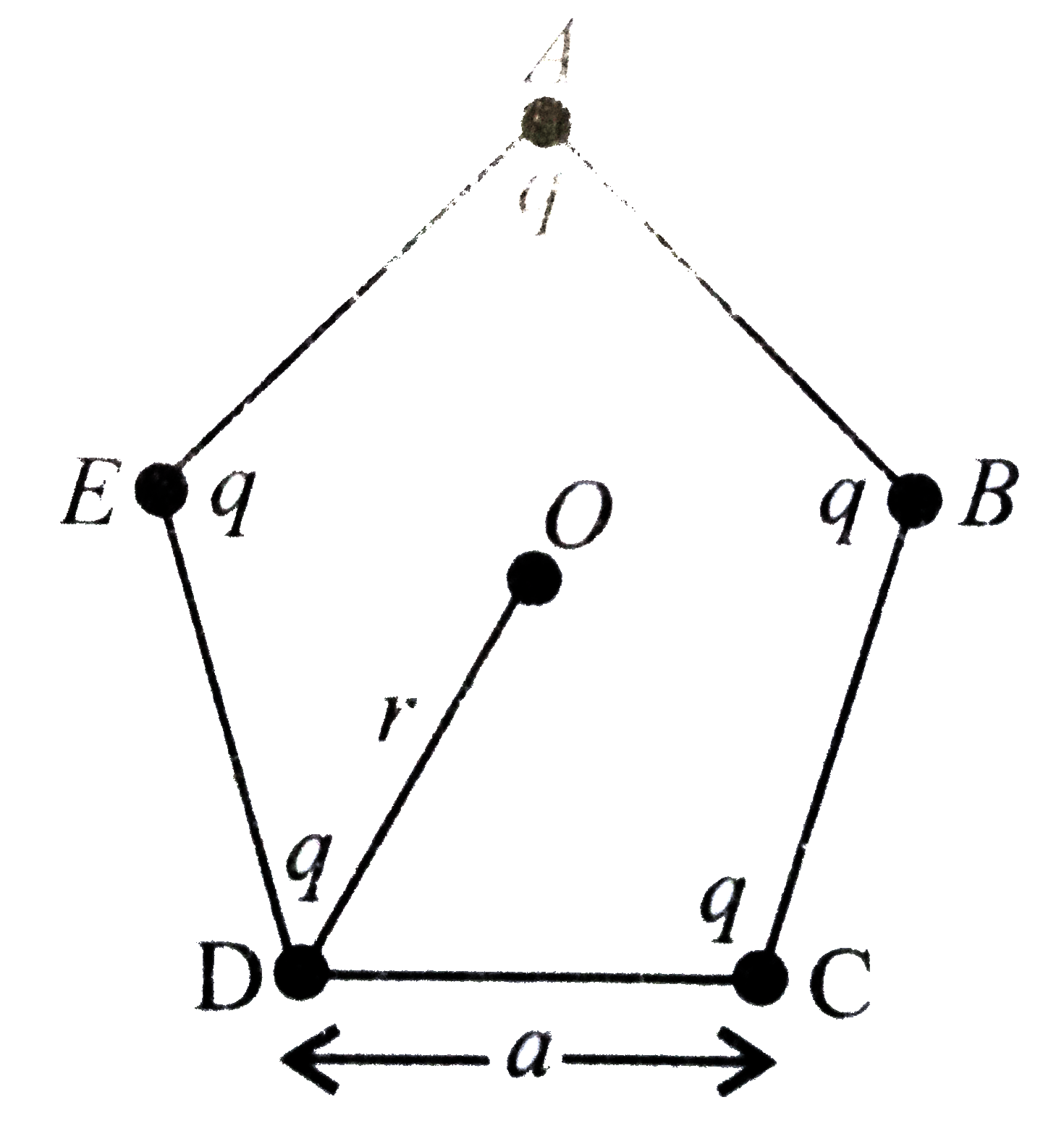
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is
View SolutionShow that any four vertices of a regular pentagon form a cyclic quadrilateral.
View Solution
