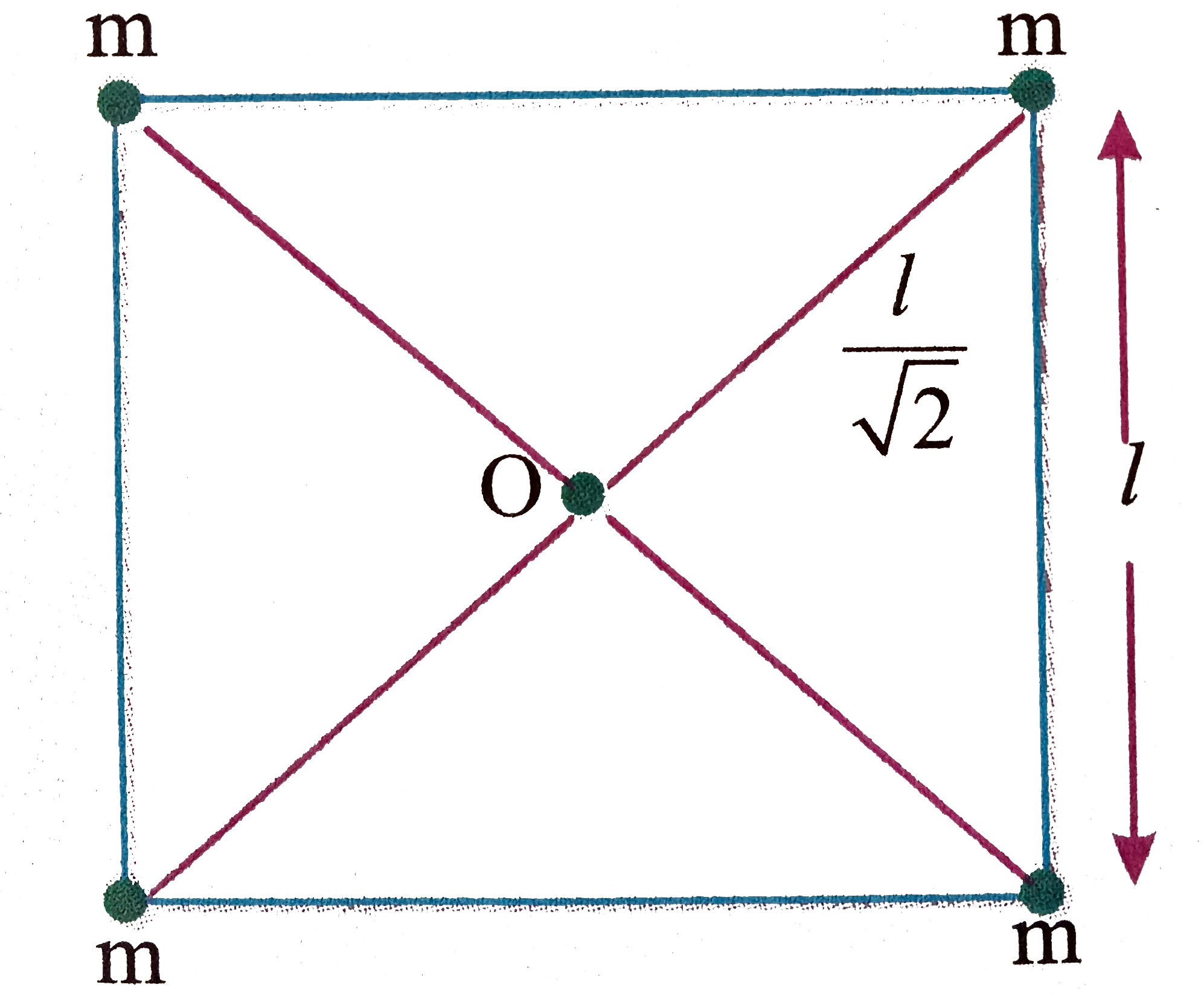
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
−2√2Gml
−3√2Gml
−2Gml
−4√2Gml
The correct Answer is:D
To find the gravitational potential at the center of a square formed by four particles each of mass m placed at the vertices, we can follow these steps:
Step 1: Understand the Setup
We have four masses m located at the corners of a square with side length l. We need to calculate the gravitational potential at the center of this square.
Step 2: Calculate the Distance from the Center to a Vertex
The center of the square is equidistant from all four vertices. To find this distance, we can use the Pythagorean theorem. The distance from the center to any vertex (let's say vertex A) can be calculated as follows:
- The coordinates of the vertices can be taken as (0,0), (l,0), (0,l), and (l,l).
- The center of the square is at (l2,l2).
- The distance d from the center to a vertex (for example, vertex A at (0,0)) is given by:
d=√(l2−0)2+(l2−0)2=√(l2)2+(l2)2=√l24+l24=√l22=l√2
Step 3: Write the Formula for Gravitational Potential
The gravitational potential V due to a mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
Step 4: Calculate the Total Potential at the Center
Since potential is a scalar quantity, we can simply add the potentials due to each mass at the center. The distance from the center to each mass is l√2.
Thus, the total potential Vtotal at the center due to all four masses is:
Vtotal=VA+VB+VC+VD=−Gml√2−Gml√2−Gml√2−Gml√2
Vtotal=−4⋅Gml√2=−4Gm√2l
Final Answer
The potential at the center of the square is:
Vtotal=−4Gm√2l
---
We have four masses m located at the corners of a square with side length l. We need to calculate the gravitational potential at the center of this square.
The center of the square is equidistant from all four vertices. To find this distance, we can use the Pythagorean theorem. The distance from the center to any vertex (let's say vertex A) can be calculated as follows:
- The center of the square is at (l2,l2).
- The distance d from the center to a vertex (for example, vertex A at (0,0)) is given by:
d=√(l2−0)2+(l2−0)2=√(l2)2+(l2)2=√l24+l24=√l22=l√2
The gravitational potential V due to a mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
Since potential is a scalar quantity, we can simply add the potentials due to each mass at the center. The distance from the center to each mass is l√2.
Vtotal=VA+VB+VC+VD=−Gml√2−Gml√2−Gml√2−Gml√2
Vtotal=−4⋅Gml√2=−4Gm√2l
The potential at the center of the square is:
Vtotal=−4Gm√2l
Topper's Solved these Questions
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Motion Of Satellite
33 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Problems Based On Mixed Concepts
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Field And Acceleration Due To Gravity
34 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
Find the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View Solution
Knowledge Check
Four particle of mass m each are placed at four corners of a square ABCD of side a. Point O is the centre of the square. Moment of inertia of all four particles about an axis passing through
AA and B is 2ma2BA and C is ma2CO and perpendicular to plane of square is 2ma2DO and parallel to CD is ma2Four particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system about an axis perpendicular to the plane of square and passing through its centre is
Al√2Bl2ClD√2lFour particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
A(1,1)B(−1,1)C(1,−1)D(0,0)
Four charges 10−5,−2×10−5,+3×10−5 and 2×10−5 coulomb are placed at the four corners of a square of side 1m the potential at the centre of the square is...
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find graitational potential energy of this system.
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through any side of frame is
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View Solution
