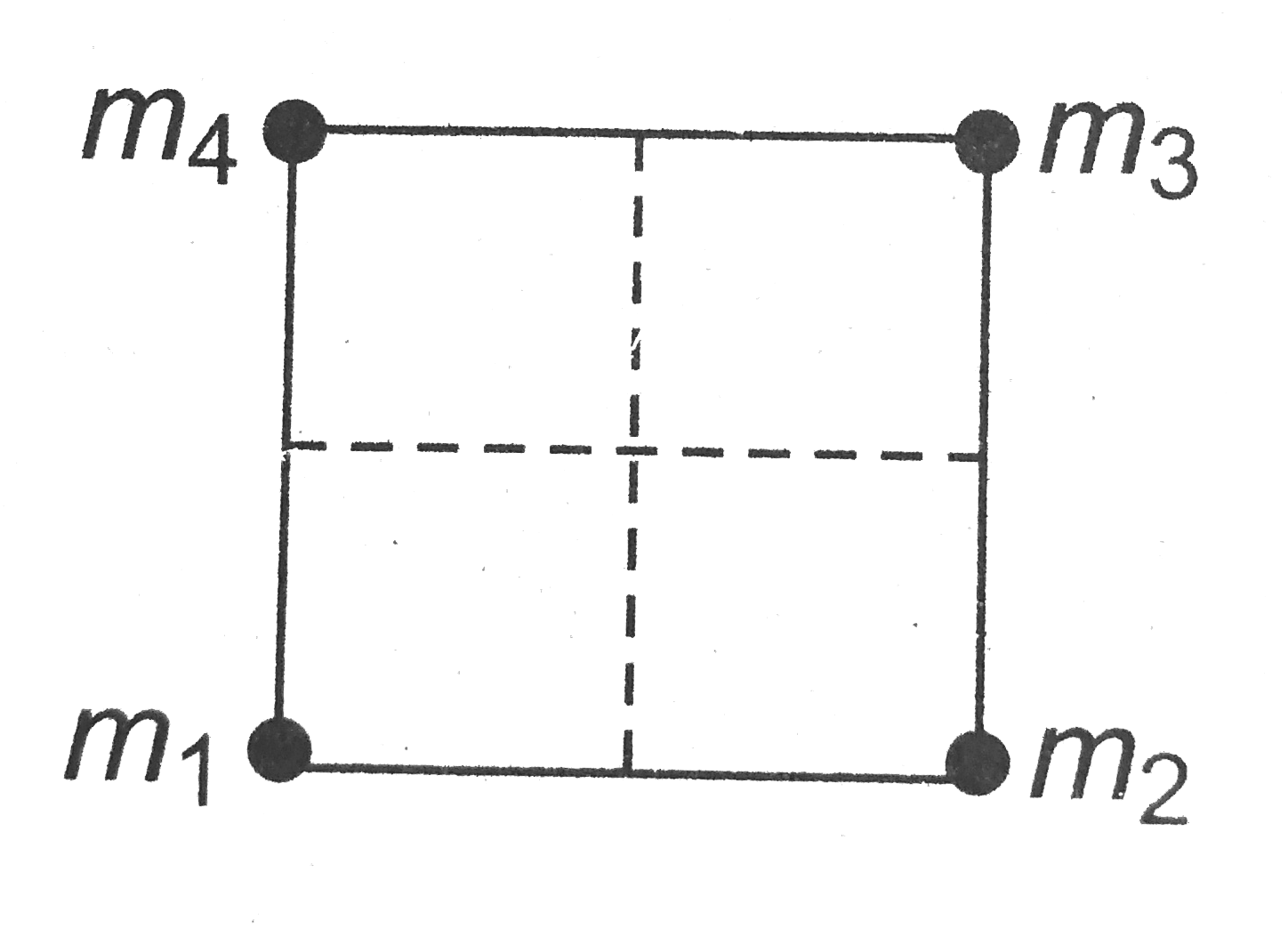
Four paticle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
Because we have particles, the magnitude of the gravitational force on particel 1 due to either of the other particles is given by Eq. 13-1 (F=Gm1m2/r2). The direction of a gravitational force on partile 1 is toward the particle responsible for the force. We can use symmetry to eliminate unneeded calculations.
Calculations : For the magnitudes of the forces on partice 1,first note that particles 2 and 4 have equal masses and equal distance of r = 2a from particle 1. Thus, form Eq. 13-1, we find that
F12=F14=Gm1m3(2a)2(13−9)
Similarly, since particles 3 and 5 have equal masses and are both at distance r = a from particle 1, we find
F13=F15=Gm1m3a2 (13-10)
We could now substicute known data into these two equations to evaluate the magnitude of the forces,indicate thedireactionof the fores on the free-body diagram of Fig. 13-5b,and then find the net force either (1) by resolving the vectors into x and y components, finding the net x andnet y components, and then vectorially combining tem or (2) by adding the vectors directly on a vector-capable calculator.
Instead, however, we shall make further use of the symmetry of the problem. First, we note that →F12and→F14 are equal inmagnitude but opposite in direaction, thus, those forces cancel. Inspection of Fig. 13-5b and Eq. 13-10 reveals that the x components of →F13and→F15 also cancel, and that their y components are identicalin magnitude and both act in the positive direaction of the y axis.

Figure 13-5 (a) An arrangement of five particles. (b) The forces acting on the particle of mass m1 due to the other four particles.
Thus, →F1.net acts in that same direction, and its magnitude is twice the y component of →F13 :
F1.net=2F13cosθ=2Gm1m3a2cosθ
=2(6.67×10−11m3/Kg.s2)(8.0kg)(2.0kg)(0.020m)2cos30∘
4.6×10−6N.
Note: The presence of particle 5 along the line between partiicles 1 and 4 does not alter the gravitational force on particel 1 from particle 4.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT5videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PROBLEMS63videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
Similar Questions
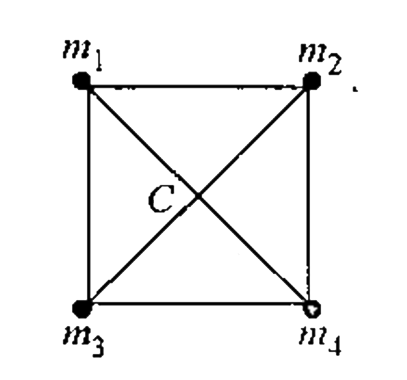
Four particle of masses m1=2kg,m2=4kg,m3=1kg and m4 are placed at four corners of a square as shown in figure. Can mass of m4 be adjusted I such a way that the centre of mass of system will be at the centre of the square C.
 View Solution
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View Solution
Knowledge Check
- Question 1 - Select One
Four particles of masses m,m 2 m and 2m are placed at the four corner of a squre of side a as shown in figure -4. 107. The (x,y) coordinates of the centre of mass are:
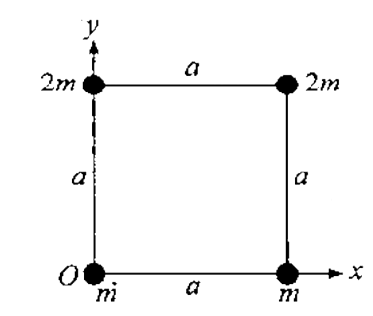 A(a2,2a)B(a2,a)C(a2,2a3)D(a,a3)
A(a2,2a)B(a2,a)C(a2,2a3)D(a,a3) - Question 2 - Select One
Four bodies of masses 2, 3, 5 and 8 kg are placed at the four corners of a square of side 2 m. The position of CM will be -
A(89,139)B(79,119)C(119,139)D(119,89)
Four particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
View SolutionIf four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionFour particles of masses 1 kg, 2 kg, 3 kg, 4 kg are placed at the corners of a square of side 2 m. Find the coordinates of centre of mass.
View SolutionFour particles A,B,CandD of masses m,2m,3mand4m respectively are placed at corners of a square of side x as shown in Fig.

Locate the centre of mass.View SolutionFour particles having masses, m, wm, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View Solution

