Frame S1 moves in the positive x direction at 0.6c with respect to frame S2. A particle moves in the positive x direction at 0.4c as measured by an observer in S1. The speed of the particle as measured by an observer in S2 is
c/5
5c/19
8c/25
25c/31
The correct Answer is:D
To find the speed of the particle as measured by an observer in frame S2, we can use the relativistic velocity addition formula. The formula states:
vpS2=vpS1+vS1S21+vpS1⋅vS1S2c2
Where:
- vpS2 is the speed of the particle as measured in frame S2.
- vpS1 is the speed of the particle as measured in frame S1 (which is 0.4c).
- vS1S2 is the speed of frame S1 with respect to frame S2 (which is 0.6c).
- c is the speed of light.
Step 1: Identify the speeds
From the problem:
- vpS1=0.4c
- vS1S2=0.6c
Step 2: Substitute into the formula
Substituting the values into the relativistic velocity addition formula:
vpS2=0.4c+0.6c1+(0.4c)(0.6c)c2
Step 3: Simplify the numerator
The numerator simplifies to:
0.4c+0.6c=1.0c
Step 4: Simplify the denominator
Now, simplify the denominator:
1+(0.4)(0.6)c2c2=1+0.24=1.24
Step 5: Combine the results
Now we can combine the results:
vpS2=1.0c1.24
Step 6: Calculate the final speed
Calculating the final speed:
vpS2=100c124=25c31
Conclusion
Thus, the speed of the particle as measured by an observer in frame S2 is:
vpS2=25c31
- vpS2 is the speed of the particle as measured in frame S2.
- vpS1 is the speed of the particle as measured in frame S1 (which is 0.4c).
- vS1S2 is the speed of frame S1 with respect to frame S2 (which is 0.6c).
- c is the speed of light.
From the problem:
- vpS1=0.4c
- vS1S2=0.6c
Substituting the values into the relativistic velocity addition formula:
The numerator simplifies to:
Now, simplify the denominator:
Now we can combine the results:
Calculating the final speed:
Thus, the speed of the particle as measured by an observer in frame S2 is:
Topper's Solved these Questions
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
11 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PROBLEMS
49 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
Similar Questions
The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.
View Solution
Knowledge Check
Position-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :
 A154m/sB103m/sC52m/sD54m/s
A154m/sB103m/sC52m/sD54m/sA particle moving along the x axis has a position given by x=54t−2.0t3m. At the time t=3.0s, the speed of the particle is zero. Which statement is correct ?
A4.3×104m/s2, southB9.4×104m/s2, northC5.1×104m/s2, northD2.2×103m/s2, southTwo events occur simultaneously at separated points on the y axis of reference frame S. According to an observer moving in the positive x direction
AThe event with the greater y coordinate occurs firstBThe event with the greater y coordinate occurs lastCEither event might occur first, depending on the observer's speedDThe events are simultaneous
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View SolutionAt a certain time a particle had a speed of 18 m/s in the positive x direction, and 2.4 s later its speed was 30 m/s in the opposite direction. What is the average acceleration of the particle during this 2.4 s interval ?
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in metres and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
What is the average velocity of the particle in the time interval t=0 s to t=1 s?
View SolutionA particle is moving along positive X direction and is retarding uniformly. The particle crosses the origin at time t=0 and crosses the point x=4.0m at t=2s.
(a) Find the maximum speed that the particle can possess at x=0.
(b) Find the maximum value of retardation that the particle can have.
View SolutionThe velocityof a particle that moves in the positive X- direction varies with its position, as shown in figure-1.22. Find its acceleration in m/s2 where x=6m
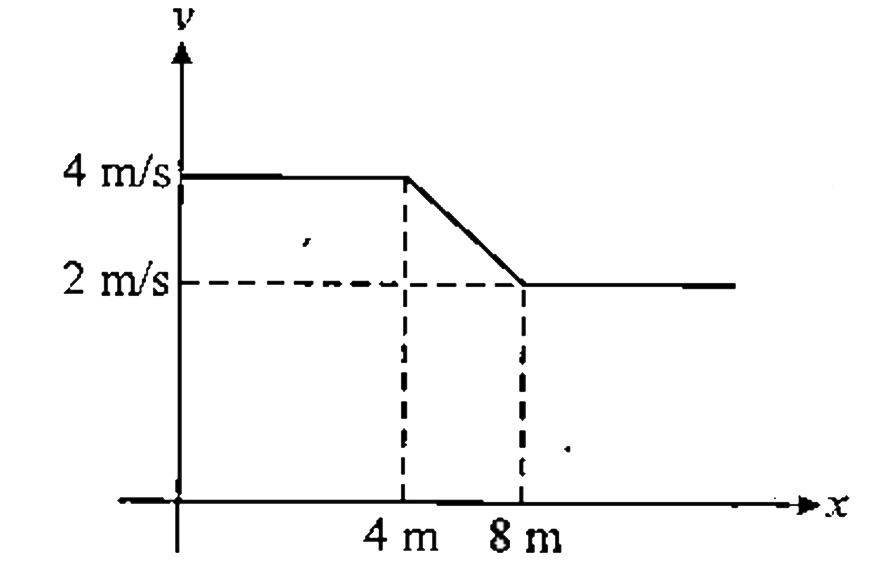
View Solution
