Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/s2
2πms
πms
1πms
12π/ms
The correct Answer is:D
Mean position of the particle is mgk distance below the unstretched position of spring. Therefore aplitude of oscillation A=mgk
ω=√km=2πf=20π(f=10Hz)
mk=1400π2
vmax=Aω=g400π2×20π=12πms
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretched by 0.20 cm. Take g=π2ms−2
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View Solution
Knowledge Check
The kinetic energy of a particle, executing S.H.M. is 16 J when it is in its mean position. IF the amplitude of oscillation is 25 cm and the mass of the particle is 5.12 Kg, the time period of its oscillations is
Aπ/5 secB2πsecC20πsecD5π sec
A mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, g=10m/s2 )
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
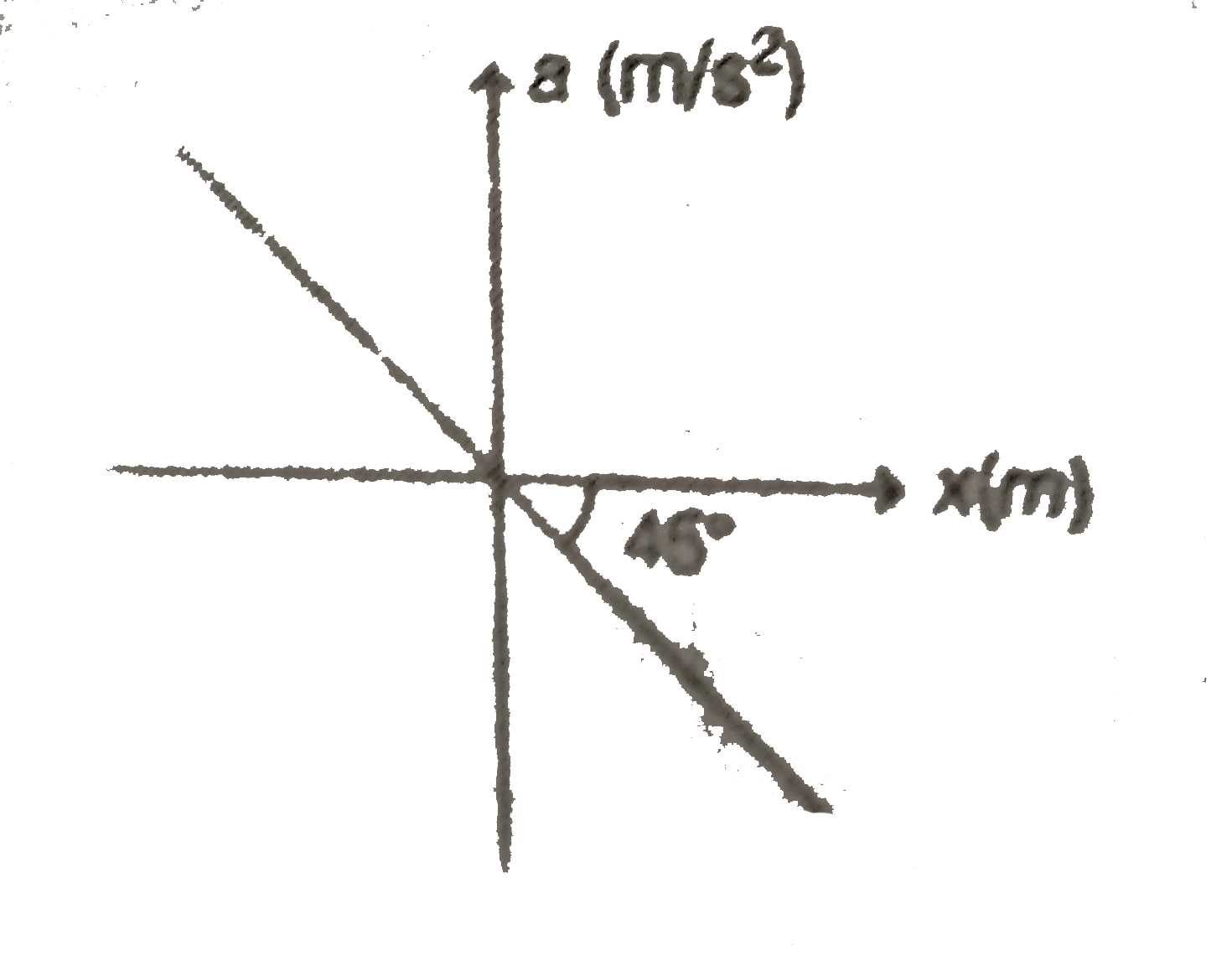
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionThe potential energy of a particle executing SHM varies sinusoidally with frequency f. The frequency of oscillation of the particle will be
View SolutionA particle executing SHM has a maximum speed of 30cm/s and a maximum acceleration of 60cms2 . The period of oscillation is
View Solution
