Amplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
2aT
2π√aT
2πaT
4aT
The correct Answer is:3
To find the maximum speed of a particle executing Simple Harmonic Motion (SHM) with amplitude a and time period T, we can follow these steps:
Step 1: Understand the SHM Equation
The position of a particle in SHM can be described by the equation:
x(t)=asin(ωt+ϕ)
where:
- x(t) is the position of the particle at time t,
- a is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
Step 2: Determine the Angular Frequency
The angular frequency ω is related to the time period T by the formula:
ω=2πT
Step 3: Find the Velocity
The velocity v(t) of the particle is the derivative of the position with respect to time:
v(t)=dxdt=aωcos(ωt+ϕ)
Step 4: Find Maximum Speed
The maximum speed vmax occurs when cos(ωt+ϕ) is at its maximum value, which is 1. Thus:
vmax=aω
Step 5: Substitute for Angular Frequency
Now, substituting ω from Step 2 into the equation for maximum speed:
vmax=a(2πT)
This simplifies to:
vmax=2πaT
Conclusion
The maximum speed of the particle executing SHM is:
vmax=2πaT
The position of a particle in SHM can be described by the equation:
x(t)=asin(ωt+ϕ)
where:
- x(t) is the position of the particle at time t,
- a is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
The angular frequency ω is related to the time period T by the formula:
ω=2πT
The velocity v(t) of the particle is the derivative of the position with respect to time:
v(t)=dxdt=aωcos(ωt+ϕ)
The maximum speed vmax occurs when cos(ωt+ϕ) is at its maximum value, which is 1. Thus:
vmax=aω
Now, substituting ω from Step 2 into the equation for maximum speed:
vmax=a(2πT)
This simplifies to:
vmax=2πaT
The maximum speed of the particle executing SHM is:
vmax=2πaT
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Knowledge Check
The kinetic energy of a particle, executing S.H.M. is 16 J when it is in its mean position. IF the amplitude of oscillation is 25 cm and the mass of the particle is 5.12 Kg, the time period of its oscillations is
Aπ/5 secB2πsecC20πsecD5π sec
The amplitude of a particle executing SHM is made three-fourth keeping its time period constant. Its total energy will be
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionThe time period of a particle executing SHM is T. After a time T/6 after it passes its mean position, then att=0 its :
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
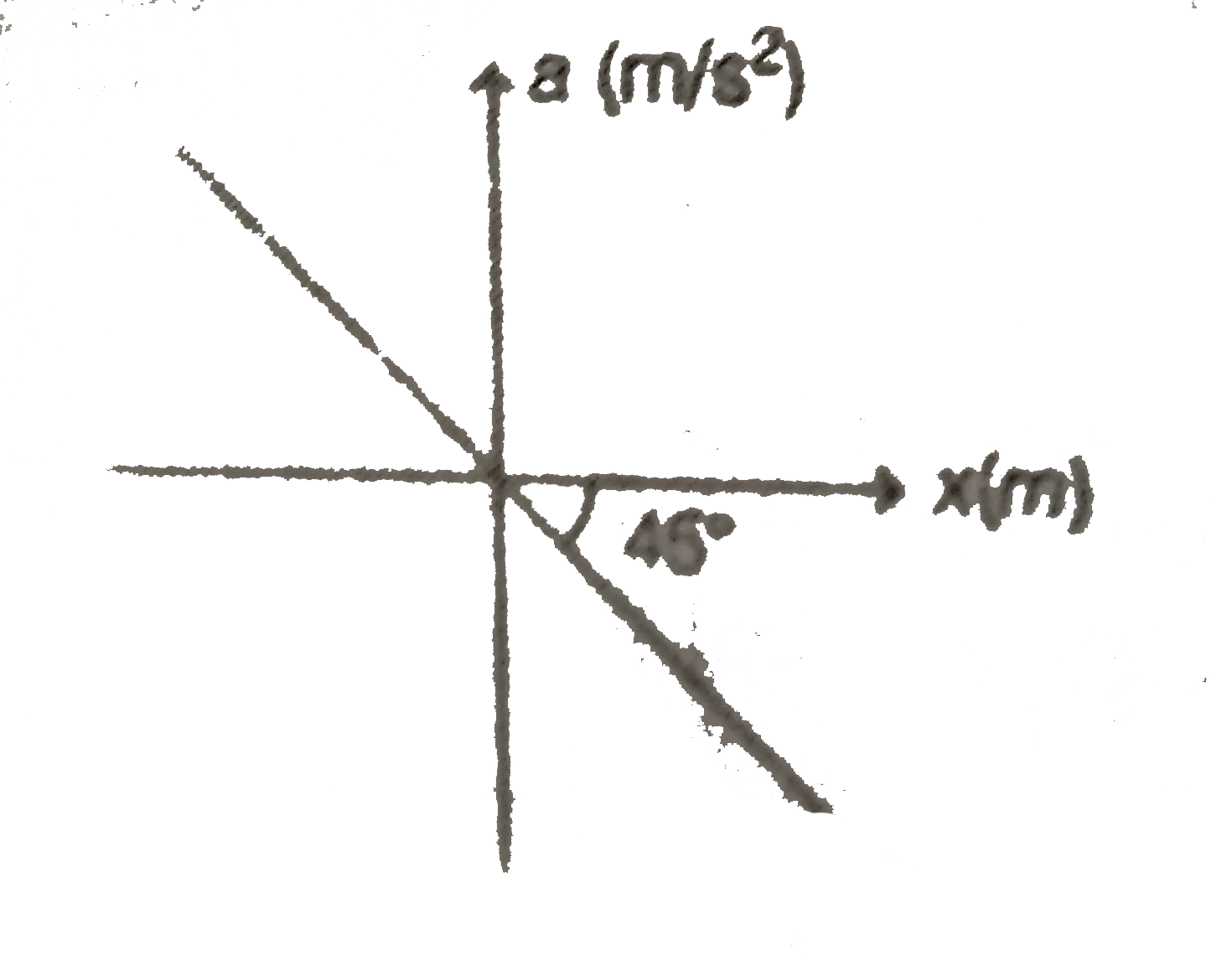
View SolutionTime period of a particle executing SHM is 16s.At time t=2s, it crosses the mean position . Its amplitude of motion is 32√2πm. Its velocity at t=4s is
View SolutionThe maximum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
View Solution
