Frequency of oscillation of a body is 6 Hz when force F1 is applied and 8 Hz when F2 is applied . If both forces F1 and F2 are applied together, then find out the frequency of oscillation.
To find the frequency of oscillation when both forces F1 and F2 are applied together, we can follow these steps:
Step 1: Understand the relationship between frequency and spring constant
The frequency of oscillation n of a mass-spring system is given by the formula:
n=12π√km
where k is the spring constant and m is the mass of the body.
Step 2: Set up the equations for the two forces
Given:
- When force F1 is applied, the frequency n1=6Hz.
- When force F2 is applied, the frequency n2=8Hz.
From the frequency formula, we can express the spring constants k1 and k2:
n1=12π√k1m⟹k1=(2πn1)2m
n2=12π√k2m⟹k2=(2πn2)2m
Step 3: Calculate k1 and k2
Substituting the values of n1 and n2:
k1=(2π⋅6)2m=144π2m
k2=(2π⋅8)2m=256π2m
Step 4: Find the resultant spring constant when both forces are applied
When both forces F1 and F2 are applied together, the effective spring constant k is:
k=k1+k2=144π2m+256π2m=(144+256)π2m=400π2m
Step 5: Calculate the resultant frequency
Using the formula for frequency with the resultant spring constant:
n=12π√km=12π√400π2mm=12π√400π2=20π2π=10Hz
Final Answer
The frequency of oscillation when both forces F1 and F2 are applied together is:
10Hz
The frequency of oscillation n of a mass-spring system is given by the formula:
n=12π√km
where k is the spring constant and m is the mass of the body.
Given:
- When force F1 is applied, the frequency n1=6Hz.
- When force F2 is applied, the frequency n2=8Hz.
n1=12π√k1m⟹k1=(2πn1)2m
n2=12π√k2m⟹k2=(2πn2)2m
Substituting the values of n1 and n2:
k1=(2π⋅6)2m=144π2m
k2=(2π⋅8)2m=256π2m
When both forces F1 and F2 are applied together, the effective spring constant k is:
k=k1+k2=144π2m+256π2m=(144+256)π2m=400π2m
Using the formula for frequency with the resultant spring constant:
n=12π√km=12π√400π2mm=12π√400π2=20π2π=10Hz
The frequency of oscillation when both forces F1 and F2 are applied together is:
10Hz
Similar Questions
Knowledge Check
Frequency of oscillation of a body is 5 Hz when a force F1 is applied and 12 Hz when another force F2 is applied. If both forces F1 and F2 are applied together, then frequency of oscillation of the body will be
A13 HzB169 HzC62 HzD52 HzOn a smooth horizontal tanle, a sphere is pressed by blocks A and B by forces F1 and F2 respectively (F1>F2) exactely normal to the tangent at the point of contact of blocks and sphere. A force F is applied on the sphere diameter OP, which is line of action of forces F1 and F2. the sphere moves out of blocks A and B. find minimum value of F. the coefficient of friction is μ at all contancts.
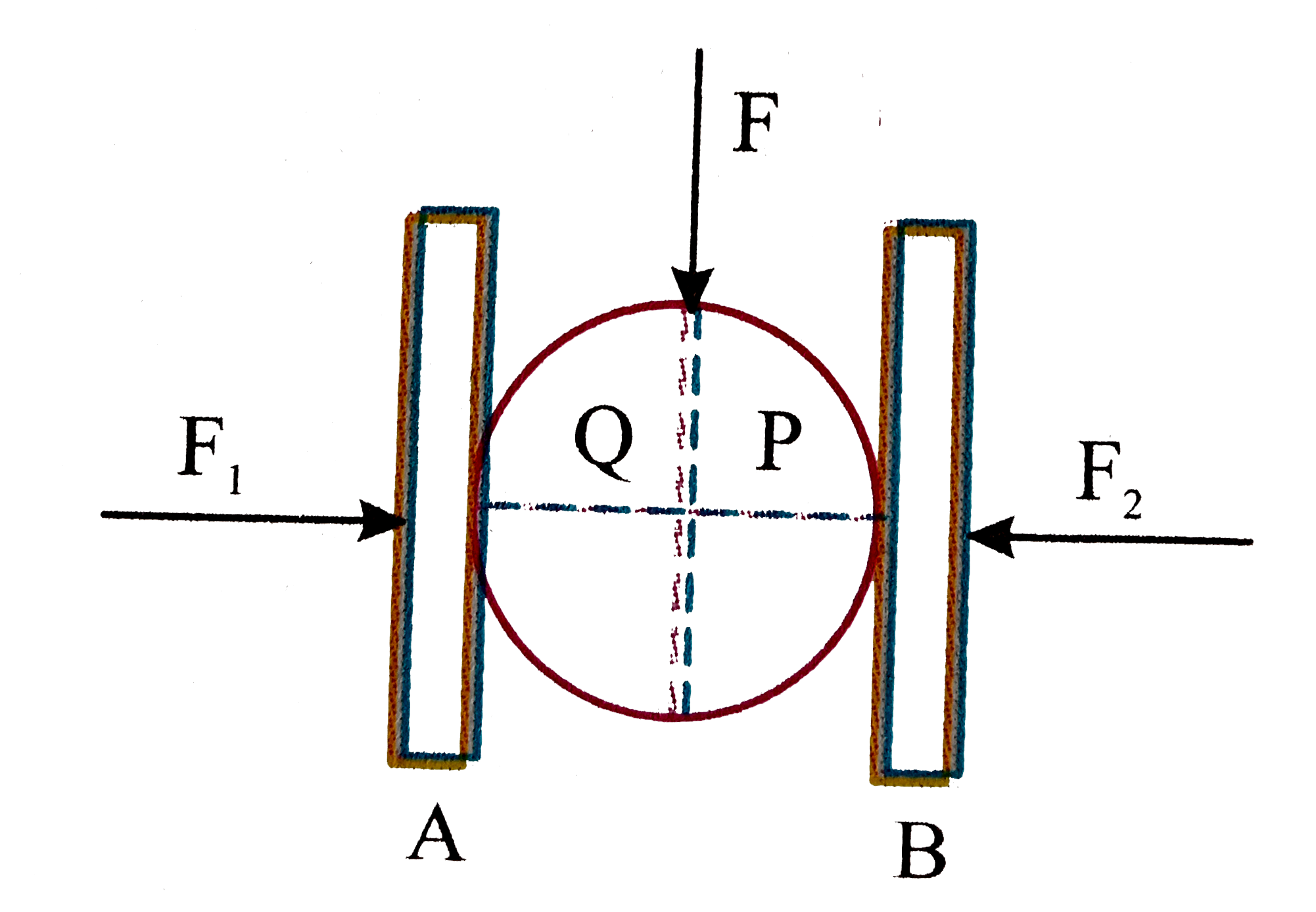 Aμ2(7F1−3F2)Bμ2(5F1−3F2)Cμ(3F1−F2)Dμ2(3F1−F2)
Aμ2(7F1−3F2)Bμ2(5F1−3F2)Cμ(3F1−F2)Dμ2(3F1−F2)When a force F acts on a body of mass m, the acceleration produced in the body is a. If three equal forces F1=F2=F3=F act on the same body as shown in figure the acceleration produced is
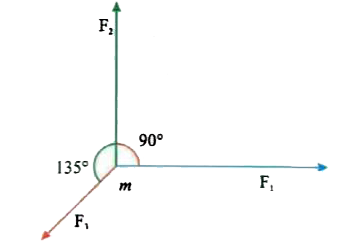 A(√2−1)aB(√2+1)C√2Da
A(√2−1)aB(√2+1)C√2Da
A wire has an elongation of 0.04m when a force F is applied on it . Now its length & diameter are double and same force F is applied on it. Find new elongation in the wire
View SolutionBlock B of mass m has been placed on block A of mass 3 m as shown. Block A rests on a smooth horizontal table. F1 is the maximum horizontal force that can be applied on the block A such that there is no slipping between the blocks. Similarly, F2 is the maximum horizontal force that can be applied on the block B so that the two blocks move together without slipping on each other. When F1andF2 both are applied together as shown in figure.
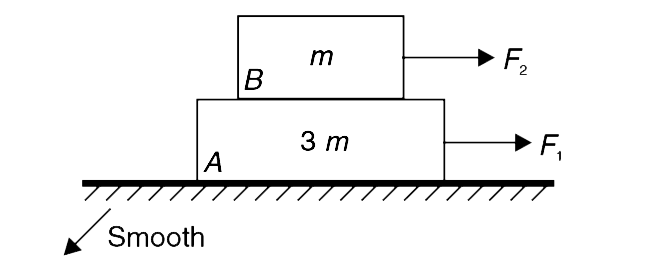
(a) Find the friction force acting between the blocks.
(b) Acceleration of the two blocks.
(c) If F2 is decreased a little, what will be direction of friction acting on B.
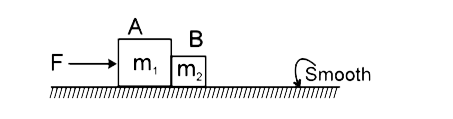
View SolutionA force F is applied horizontally on mass m1 as shown in figure. Find the contact force between m1 and m2
View SolutionA body is executing simple harmonic motion under the action of a force F1 with time period 1 s. The time period is 2s when body is acted by another force F3. What will be the total time period when both the forces are acting in same direction simultaneously ?
View SolutionA yo-yo is resting on a perfectly rough horizontal table . Forces F1,F2andF3 are applied seqarately as shown . The correct statement is
View Solution
