From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
Rπ−2
Rπ
R2(2π−1)
R2
Step by step video & image solution for From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Only one option is correct for JEE Advanced
Explore 55 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:More a than one option is Correct
Explore 1 Video
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
From a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View Solution
Knowledge Check
From the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
 AˆiR5+ˆjR5B(b) −ˆiR5+ˆjR5C(c) −ˆiR5−ˆjR5D(d) None of the above
AˆiR5+ˆjR5B(b) −ˆiR5+ˆjR5C(c) −ˆiR5−ˆjR5D(d) None of the aboveA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
A13B12C16D14From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
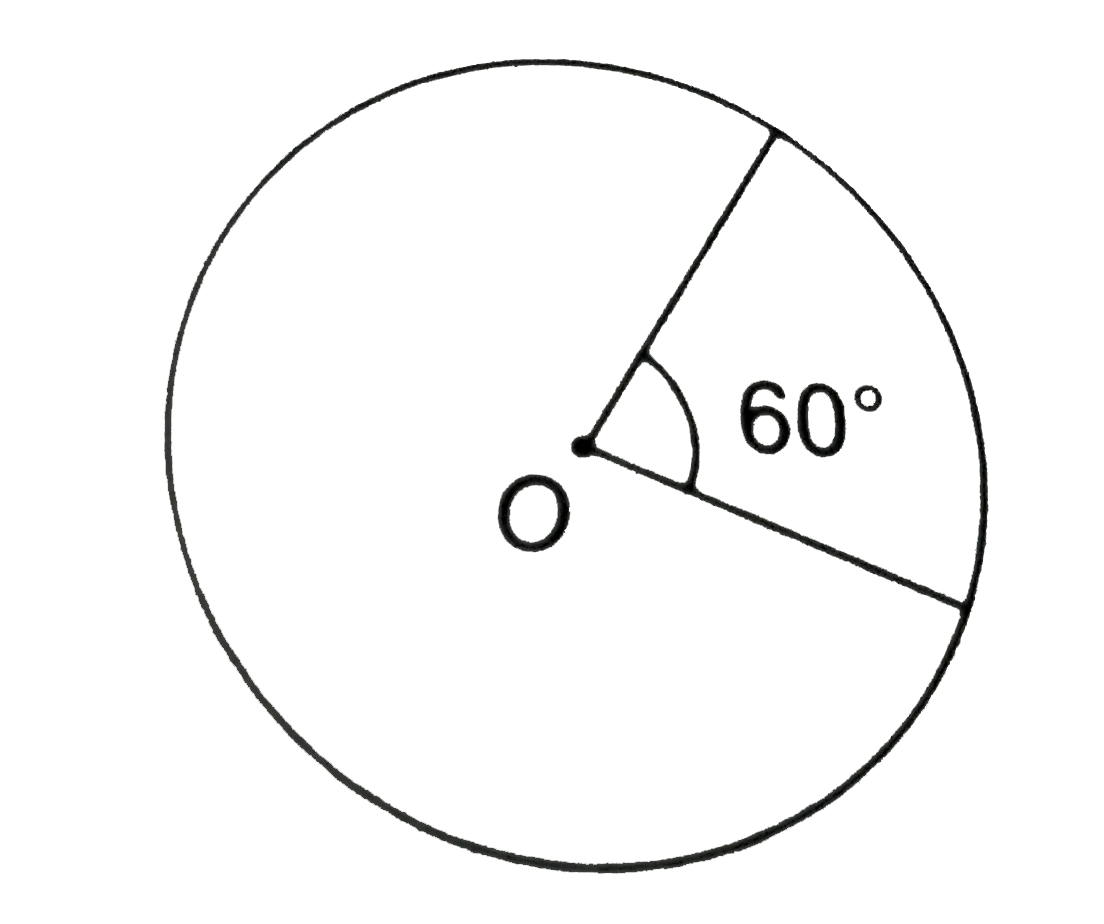 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2
From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
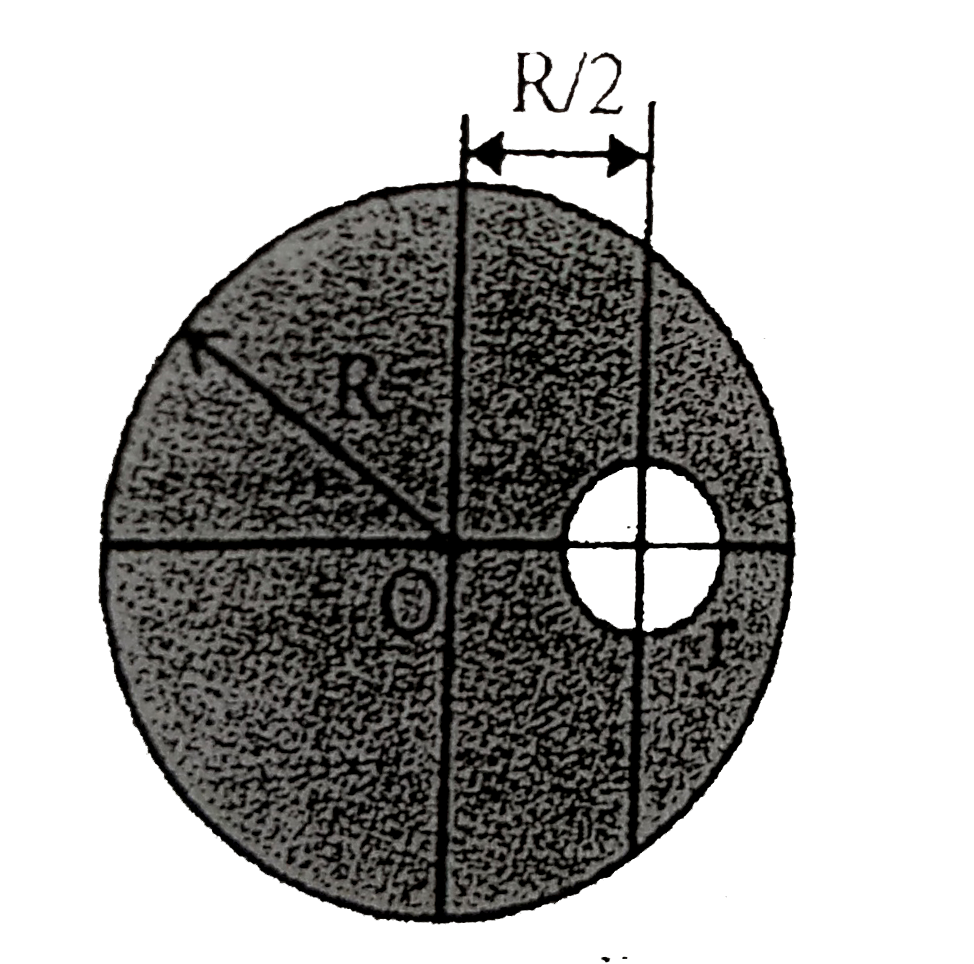
View Solution