From a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
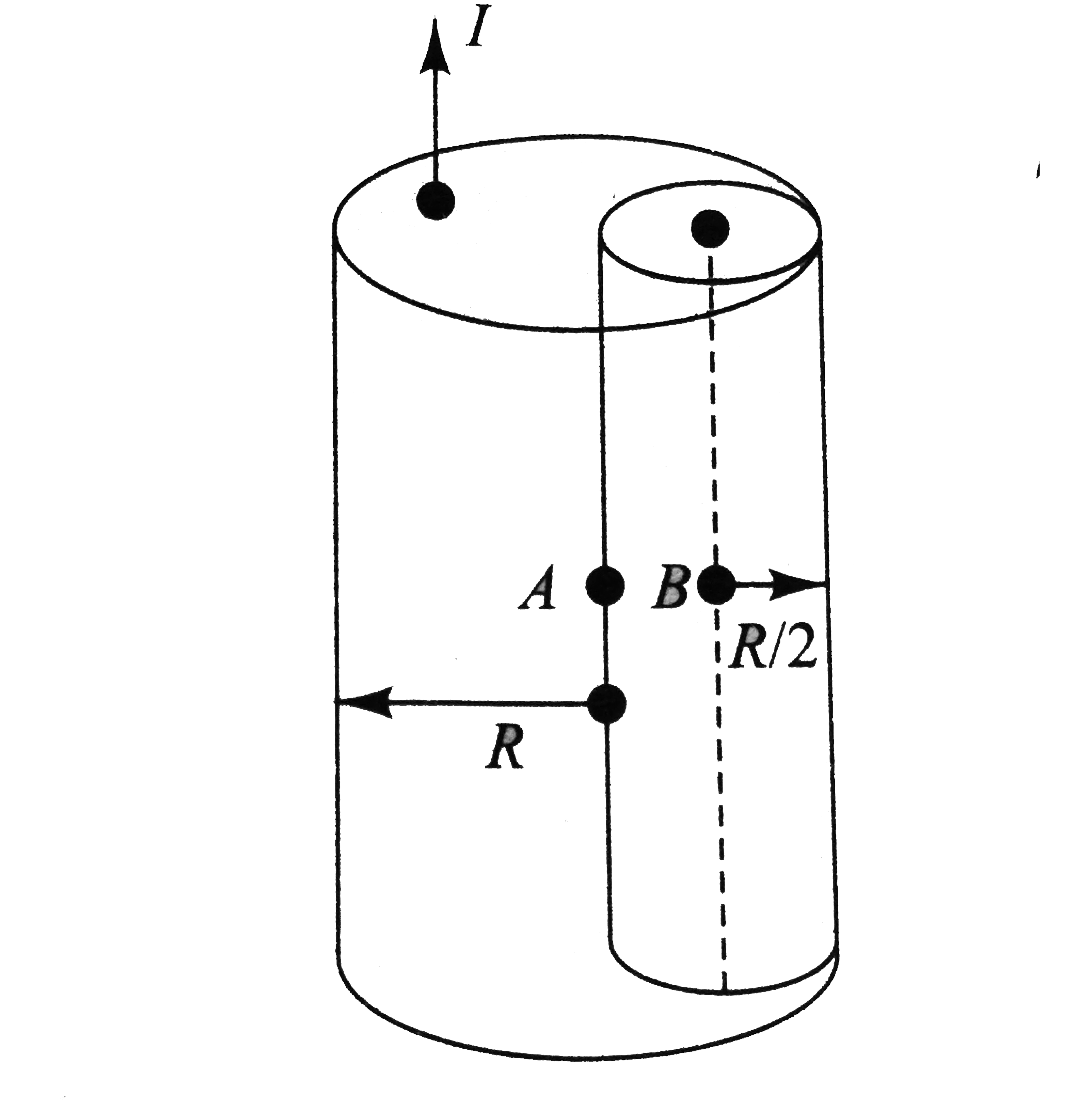
zero at point A
zero at point B
μoI3πR at point A
μoI3πR at point B
The correct Answer is:D
For cylinder:
B=μ0ir2πR2,r<a
=μ0i2πR2,r≥a
We can consider the given cylinder as a combination of two cylinders. One of radius 'R' carrying current I in the one direction and other of radius R2 carrying current I3 in both directions.
At point A:B=μ0(1/3)2π(R/2)+0=μ0I3πR
At point B:B=μ02π(4I/3πR2)(R2)+0=μ0I3πR
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts
32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current
44 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A cylinder of radius R1 have cylinderical cavity of radius R2 as shown in the figure and have current density J (down ward). Find Magnetic field when
when point is in cavity
View SolutionA cylinder of radius R1 have cylinderical cavity of radius R2 as shown in the figure and have current density J (down ward). Find Magnetic field when
r>R1 (on x-axis towards right)
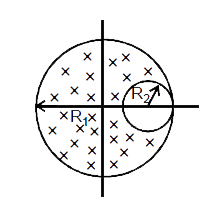
View Solution
Knowledge Check
From a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :
 Azero at point ABzero at point BCμ0I3πR at point ADμ0I3πR at point B
Azero at point ABzero at point BCμ0I3πR at point ADμ0I3πR at point BA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is
 Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)
Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-AρR6ε0BρR4ε0CρR2ε0DρR3ε0
There is a long cylinder of radius R having a cylindrical cavity of radius R/2 as shown in the figure. Apart from the cavity, the entire space inside the cylinder has a uniform mag- netic field parallel to the axis of the cylinder. The magnetic field starts changing at a uniform rate of dBdt=kT/s. Find the induced electric field at a point inside the cavity.

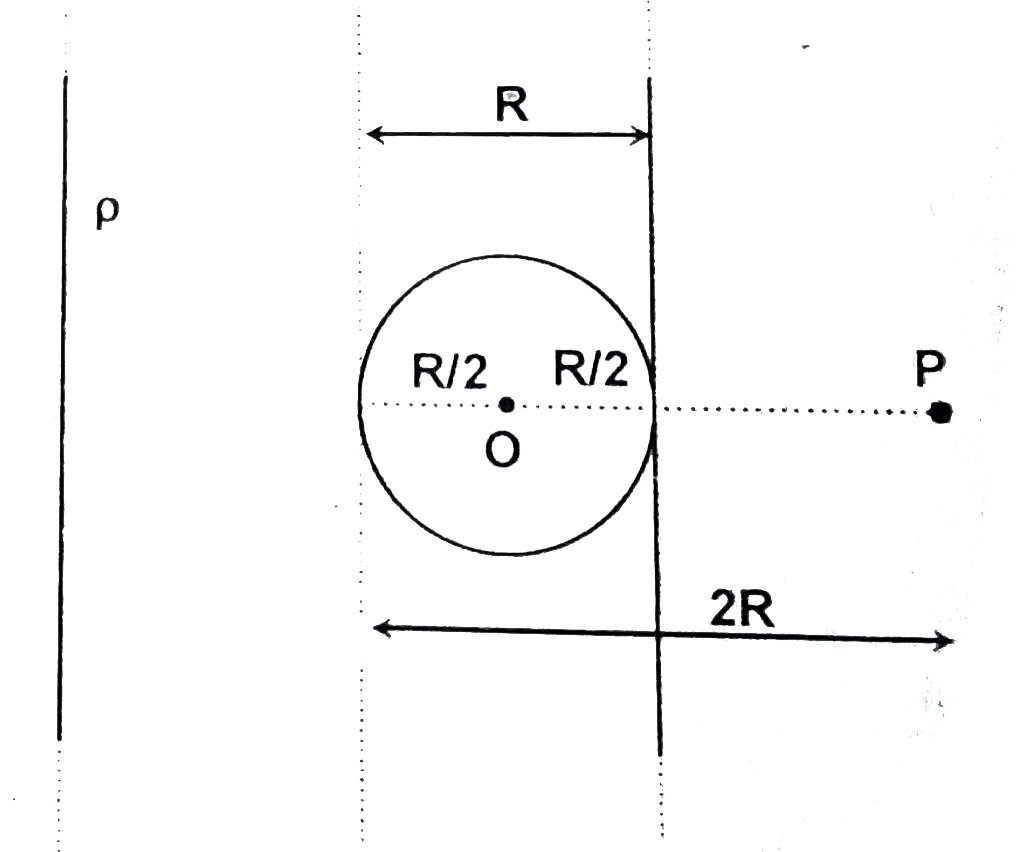
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View SolutionAn Infinite current carrying wire having current I0 is placed coaxially inside a hollow conducting infinite cylinder of radius R and having current I flowing along the length of the cylinder in the same direction as I0 what is the increment in magnetic pressure due to placing of the wire?
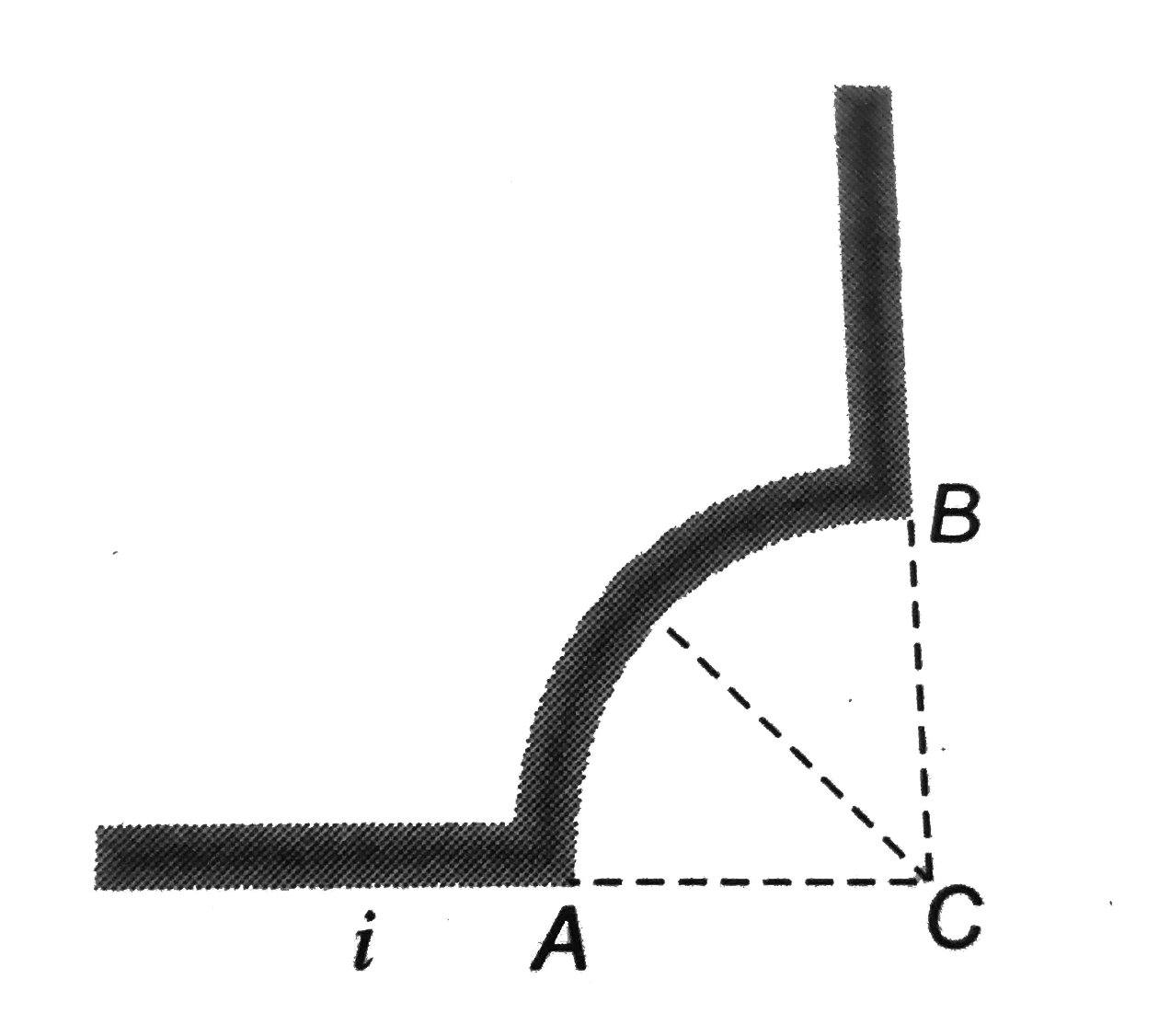
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
View Solution