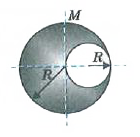
From a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?

A

$13 M R^{2} / 32$

B

$11 M R^{2} / 32$

C

$9 M R^{2} / 32$

D

$15 M R^{2} / 32$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The moment of inertia of the disc about its centre of mass, $I_{disc} = \frac{M R^{2}}{2}$
As the disc is a planar object its mass can be assumed to be uniformly distributed proportional to area. Area of original disc is four times to that of the hole.
Mass of removed part, $M . = \frac{M}{4}$
Moment of inertia of the removed part about the same axis,
$I . = \frac{M}{4} \frac{{(R / 2)}^{2}}{2} + \frac{M}{4} {(\frac{R}{2})}^{2} = \frac{3 M R^{2}}{32}$
The moment of inertia of the remaining disc =I-I.
$= \frac{M R^{2}}{2} = \frac{3}{32} M R^{2} = \frac{13}{32} M R^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a disc of radius $R$ and mass $M$ , a circular hole of diameter $R$ , whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
A $\frac{13}{32} M R^{2}$
B $\frac{11}{32} M R^{2}$
C $\frac{9}{32} M R^{2}$
D $\frac{15}{32} M R^{2}$
Question 2 - Select One
From a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A $15 M R^{2} / 32$
B $13 M R^{2} / 32$
C $11 M R^{2} / 32$
D $9 M R^{2} / 32$
Question 3 - Select One
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A $4 M^{2}$
B $\frac{40}{9} M R^{2}$
C $10 M R^{2}$
D $\frac{37}{9} M R^{2}$

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )

Home
Ask Doubt
Profile