Form a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
MR2
4MR2
49MR2
409MR2
The correct Answer is:D
To find the moment of inertia of the remaining disc after removing a smaller disc, we can follow these steps:
1. Identify the Moment of Inertia of the Original Disc:
The moment of inertia I1 of a solid disc about an axis perpendicular to its plane and passing through its center is given by the formula:
I1=12MR2
Here, the mass of the original disc is 9M and its radius is R. Thus,
I1=12×9M×R2=92MR2
2. Identify the Moment of Inertia of the Removed Disc:
The moment of inertia I2 of the smaller disc that is removed has a mass M and a radius R3. Using the same formula for the moment of inertia:
I2=12mr2
Substituting m=M and r=R3:
I2=12M(R3)2=12MR29=MR218
3. Calculate the Moment of Inertia of the Remaining Disc:
The moment of inertia of the remaining disc I is given by subtracting the moment of inertia of the smaller disc from that of the original disc:
I=I1−I2
Substituting the values we calculated:
I=92MR2−MR218
4. Finding a Common Denominator:
To subtract these fractions, we need a common denominator. The least common multiple of 2 and 18 is 18. Thus, we rewrite I1:
I1=92MR2=8118MR2
Now we can perform the subtraction:
I=8118MR2−118MR2=8018MR2
5. Simplifying the Result:
Simplifying 8018:
I=409MR2
Final Result:
The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its center is:
I=409MR2
The moment of inertia I1 of a solid disc about an axis perpendicular to its plane and passing through its center is given by the formula:
I1=12MR2
Here, the mass of the original disc is 9M and its radius is R. Thus,
I1=12×9M×R2=92MR2
The moment of inertia I2 of the smaller disc that is removed has a mass M and a radius R3. Using the same formula for the moment of inertia:
I2=12mr2
Substituting m=M and r=R3:
I2=12M(R3)2=12MR29=MR218
The moment of inertia of the remaining disc I is given by subtracting the moment of inertia of the smaller disc from that of the original disc:
I=I1−I2
Substituting the values we calculated:
I=92MR2−MR218
To subtract these fractions, we need a common denominator. The least common multiple of 2 and 18 is 18. Thus, we rewrite I1:
I1=92MR2=8118MR2
Now we can perform the subtraction:
I=8118MR2−118MR2=8018MR2
Simplifying 8018:
I=409MR2
The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its center is:
I=409MR2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
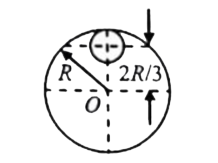
View Solution
Knowledge Check
From a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
A409MR2BMR2C4MR2D49MR2From a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
A409MR2BMR2C4MR2D49MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4M2B409MR2C10MR2D379MR2
A4M2B409MR2C10MR2D379MR2
A rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
View SolutionA semicircular disc of mass M and radius R is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
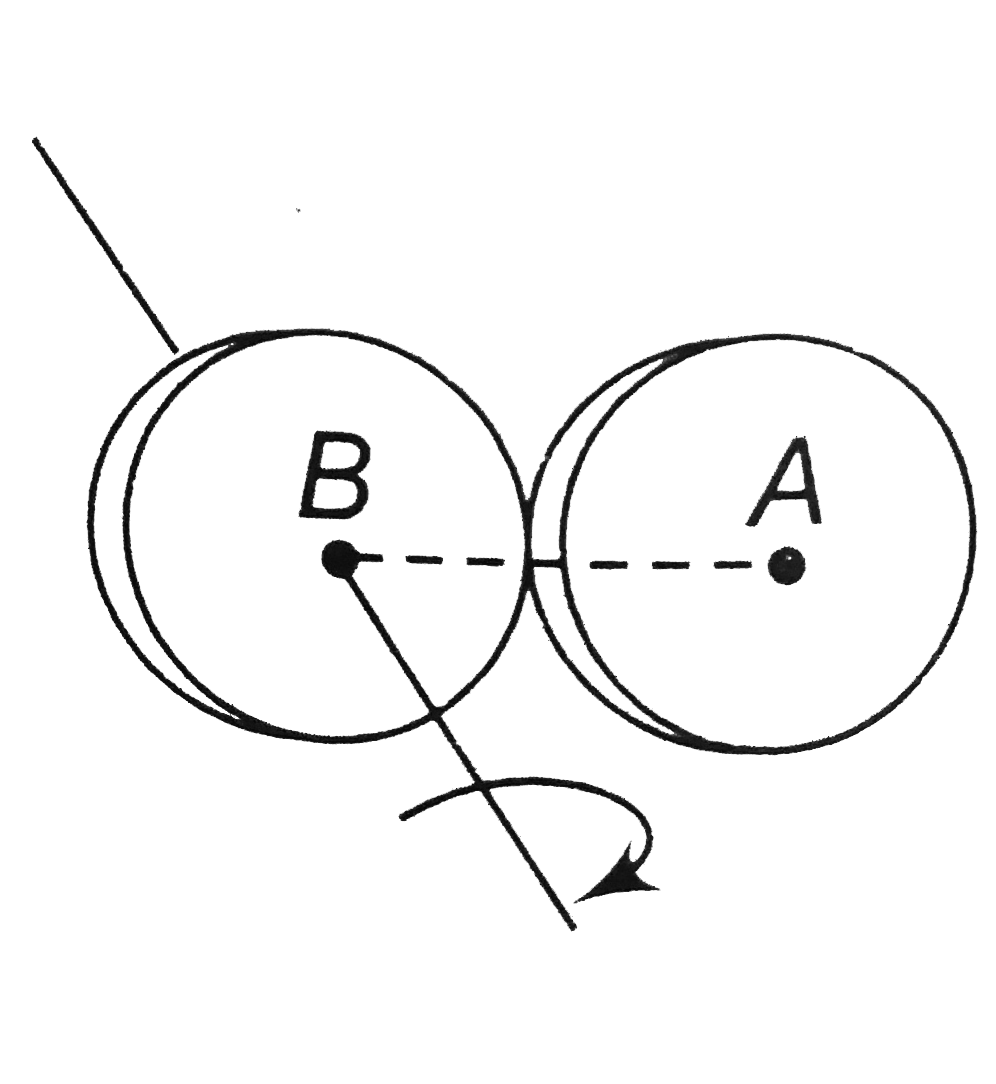 .
.
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionFrom a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View Solution