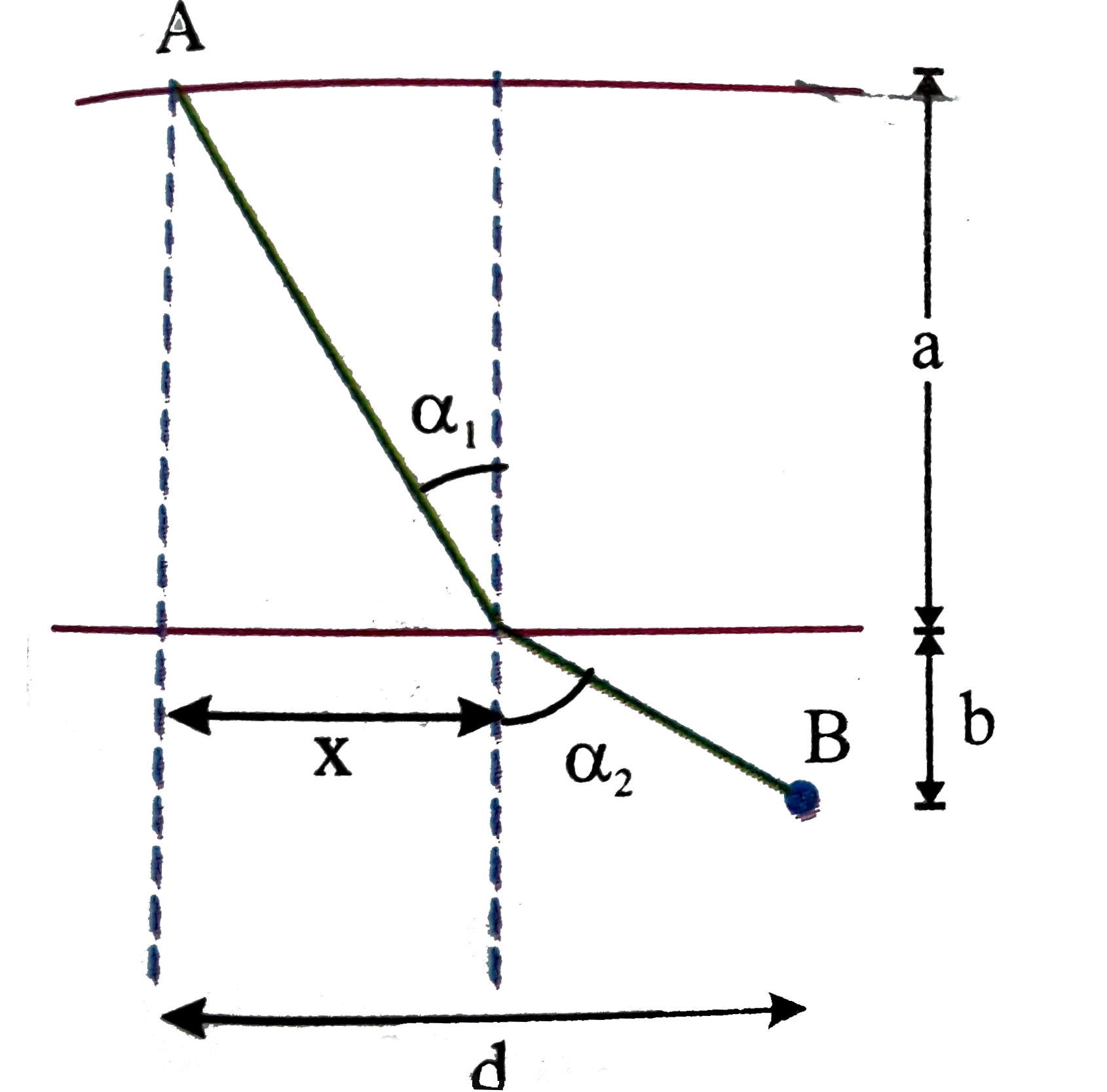
From a point A on bank of a channel with still water a person must get to a point B on the opposite bank.All the distances are shown in figure.The person uses a boat to travel across the channel and then walks along the bank of point B.The velocity of the boat is v1 and the velocity of the walking person is v2.Prove that the fastest way for the person to get from A to B is to select the angles α1 and α2 in such a manner that
sinα1sinα2=u2v1
sinα1sinα2=u1v2
cosα1cosα2=v2v1
cosα2cosα1=v1v2
The correct Answer is:a
S1=xsinα1,S2=d−xsinα2
t1=S1v1=xv1sinα1 and t2=S2v2=d−xv2sinα2
r=x[1v1sinα1−1v2sinα2]+dv2sinα2
For t be minimum dtdx=0
or 1v1sinα1=1v2sinα2,v1v2=sinα2sinα1
Topper's Solved these Questions
Similar Questions
A person travels along a straight road for the first half length with a velocity v1 and the second half length with velocity v2. What is the mean velocity of the person ?
View SolutionThe number of ways in which a person can reach from the point A to B along the grid through the shortest path as shown in the figure is -
View Solution
Knowledge Check
A man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA person swims at 135∘ to current to river, to meet target on reaching opposite point.The ratio of person's velocity to river water velocity is
A√3:1B√2:1C1:√2D1:√3A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
A9.4B2C84.6D28.2
Cash withdrawn from bank for personal use is a Contra Entry.
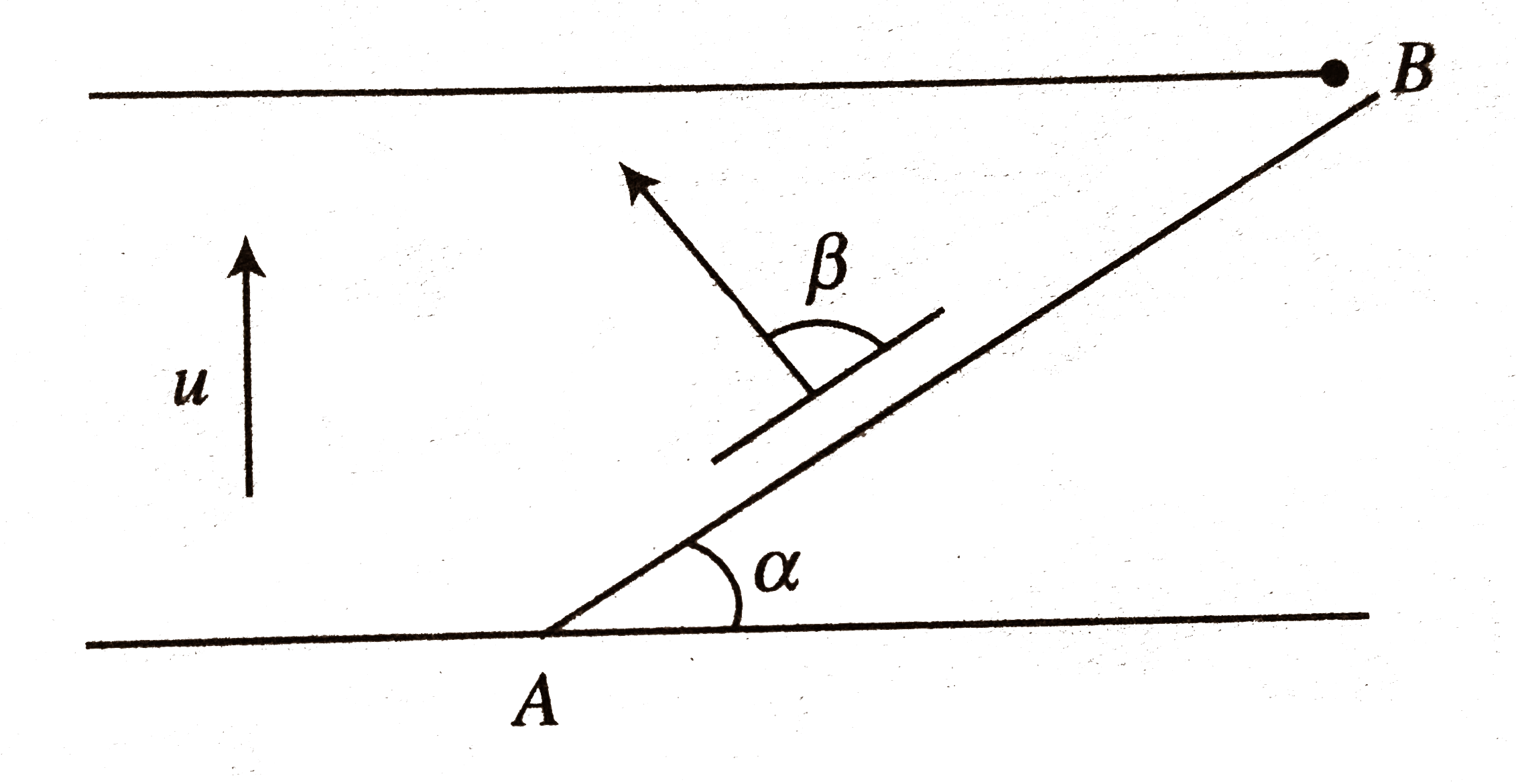
View SolutionA launch travels across a river from a point A to a point B of the opposite bank along the line AB forming angle ∝ with the bank. The flag on the mast of the launch makes an angle β with its direction of motion. Determine the speed of the launch w.r.t. the bank. The velocity of wind is u perpendicular to the stream.
 .
.
View SolutionA person starts from a point P and travels along a path PQRS as shown in the figure, then speed of the person is _____ ms−1
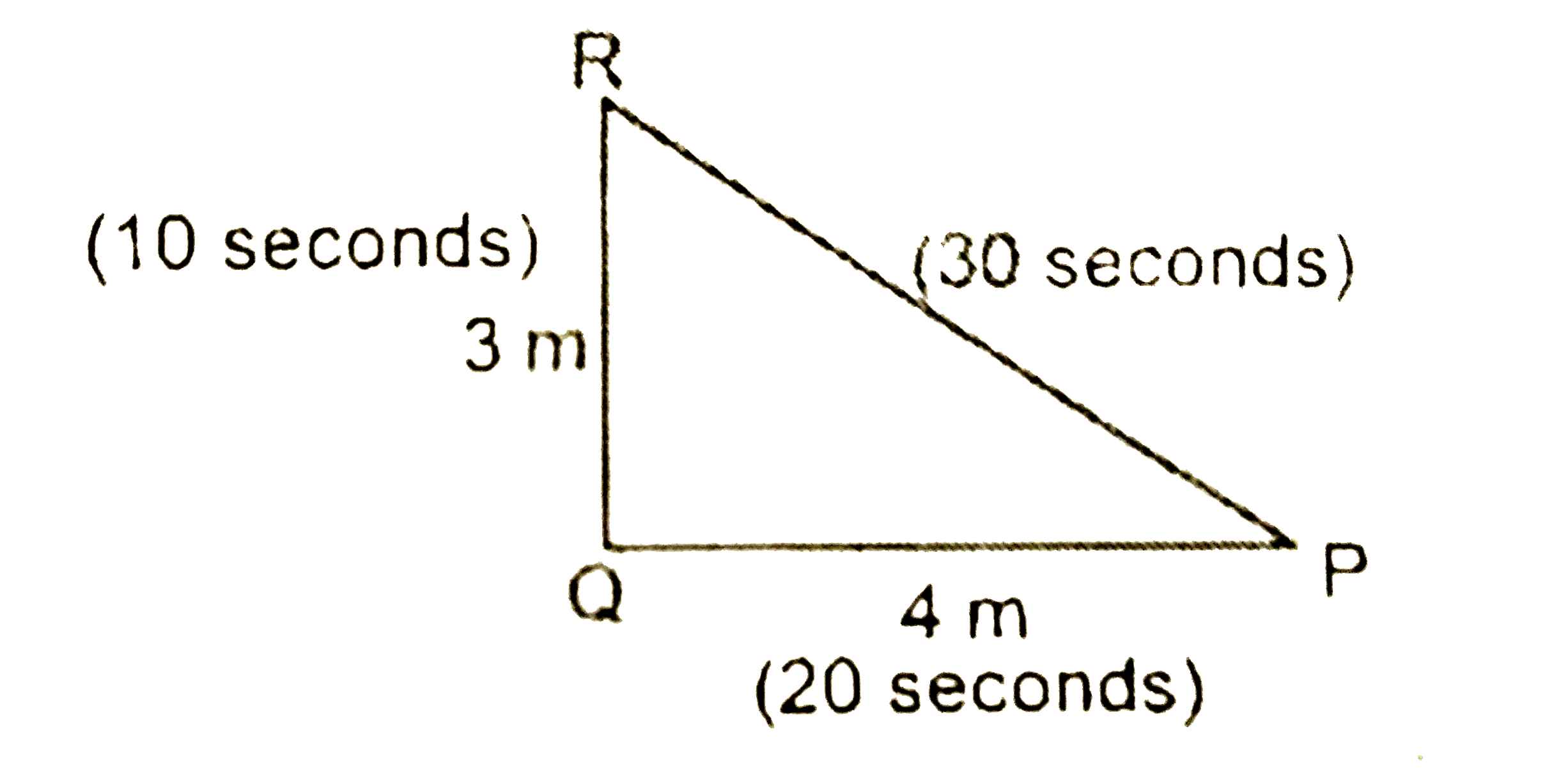
View SolutionA person starts from a point and travels along a path PQRP as shown in the figure. Then, the speed of the person is _______ms−1.
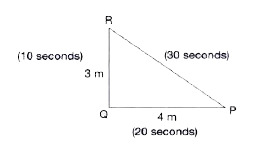
View SolutionA person starst form a point O and travels along a path PQRP as shown in the figure. Then, the speed of the operson is __________ ms−2
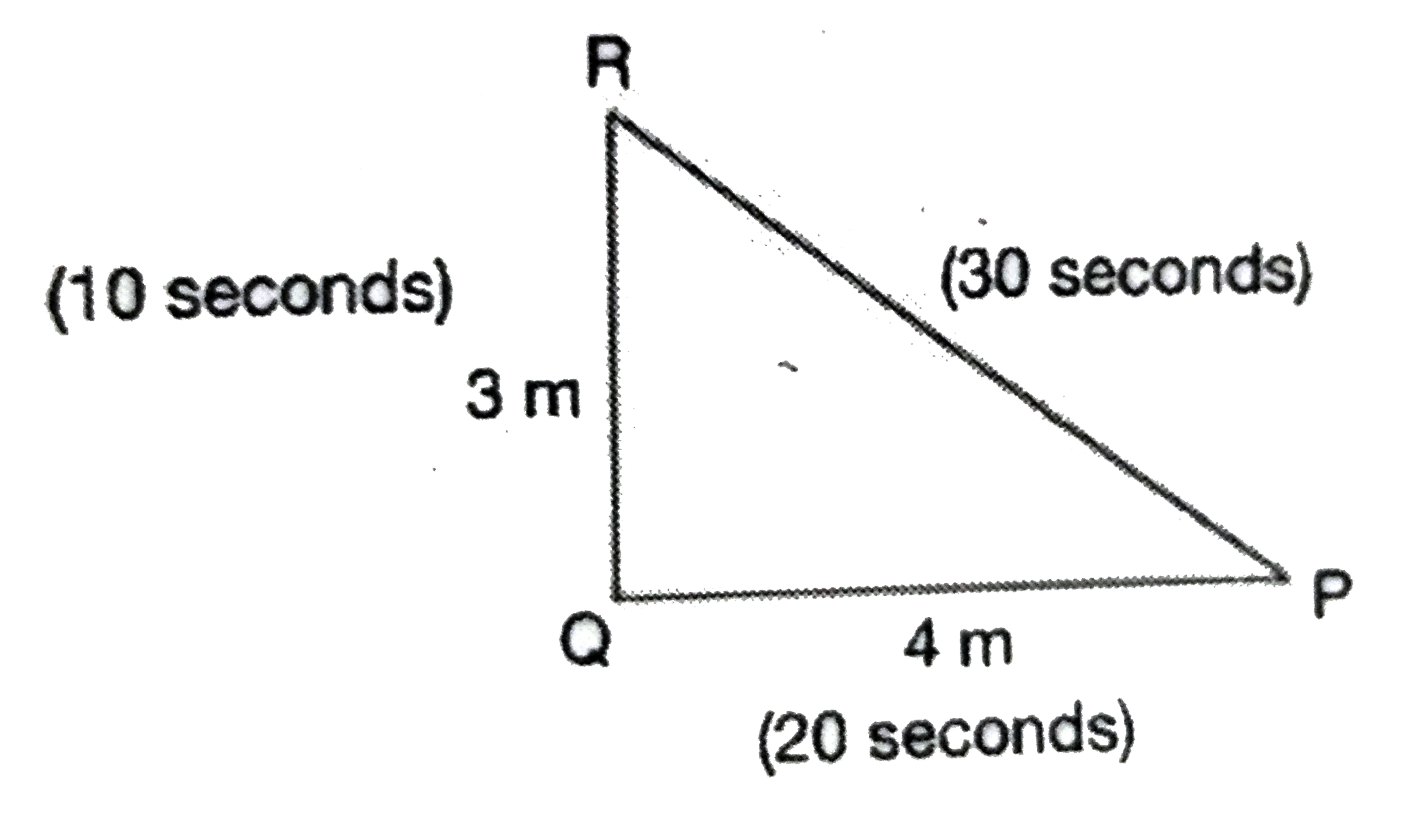
View Solution
