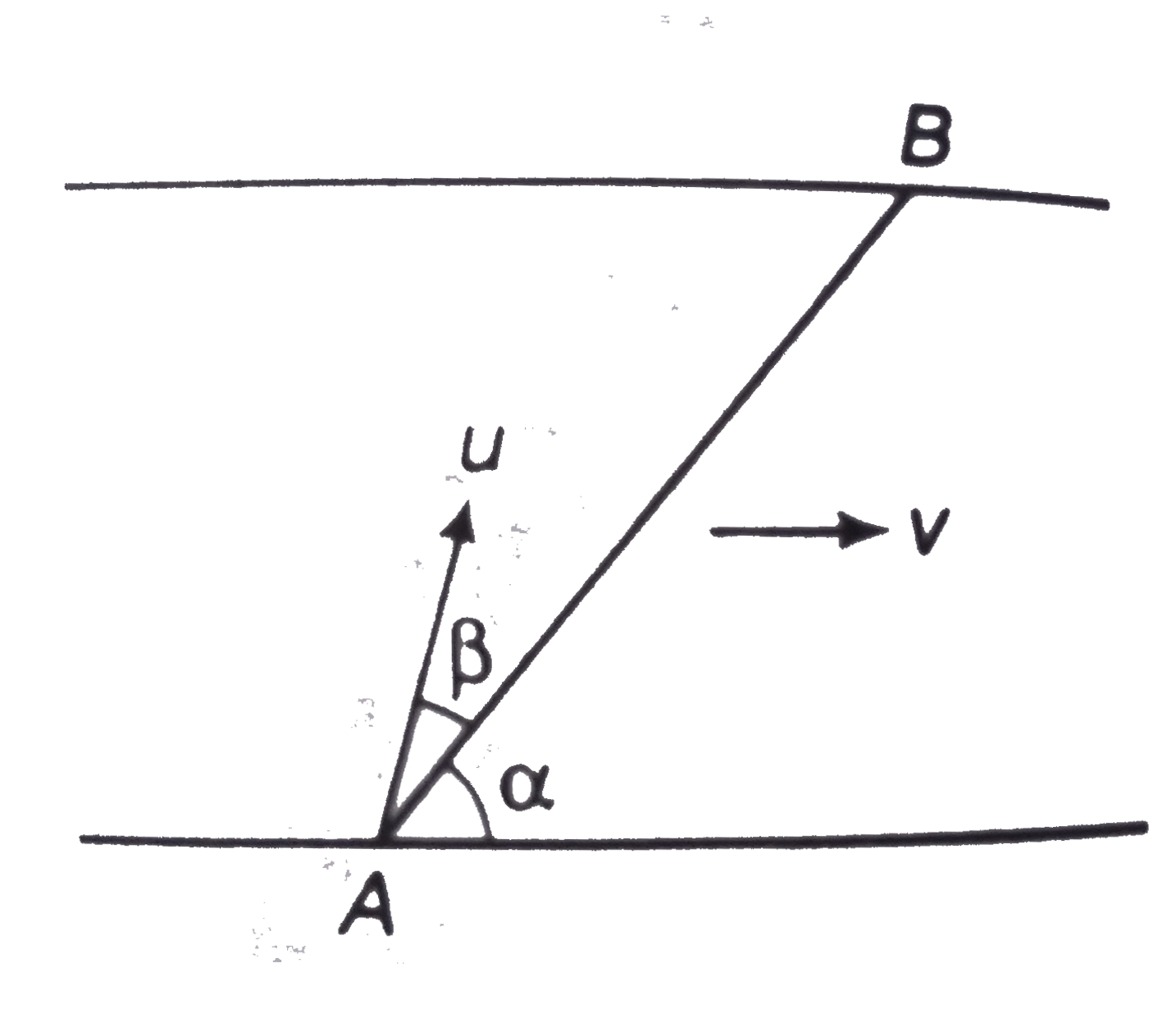
A launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
The velocity of the boat is 8m/s
The velocity of the boat is 6m/s
The angle made by u with the line AB is 12∘
The angle made by u with line AB is 10∘
The correct Answer is:b,d
In the order that the moving launch is alwy as on the straight line AB, the components of velocity of the current and of the launch in the direction perpendicu lar to AB shou ld be equal, i.e.,
usinβ=vsinα ......(i)
s=AB=(ucosβ+vcosα)t1 ........(ii)
Further BA=(ucosβ−vcosα)t2..........(iii)
t1+t2=t .........(iv)
Solving these equation after proper substitution, we get
u=8m/s and β=12∘
Topper's Solved these Questions
Similar Questions
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
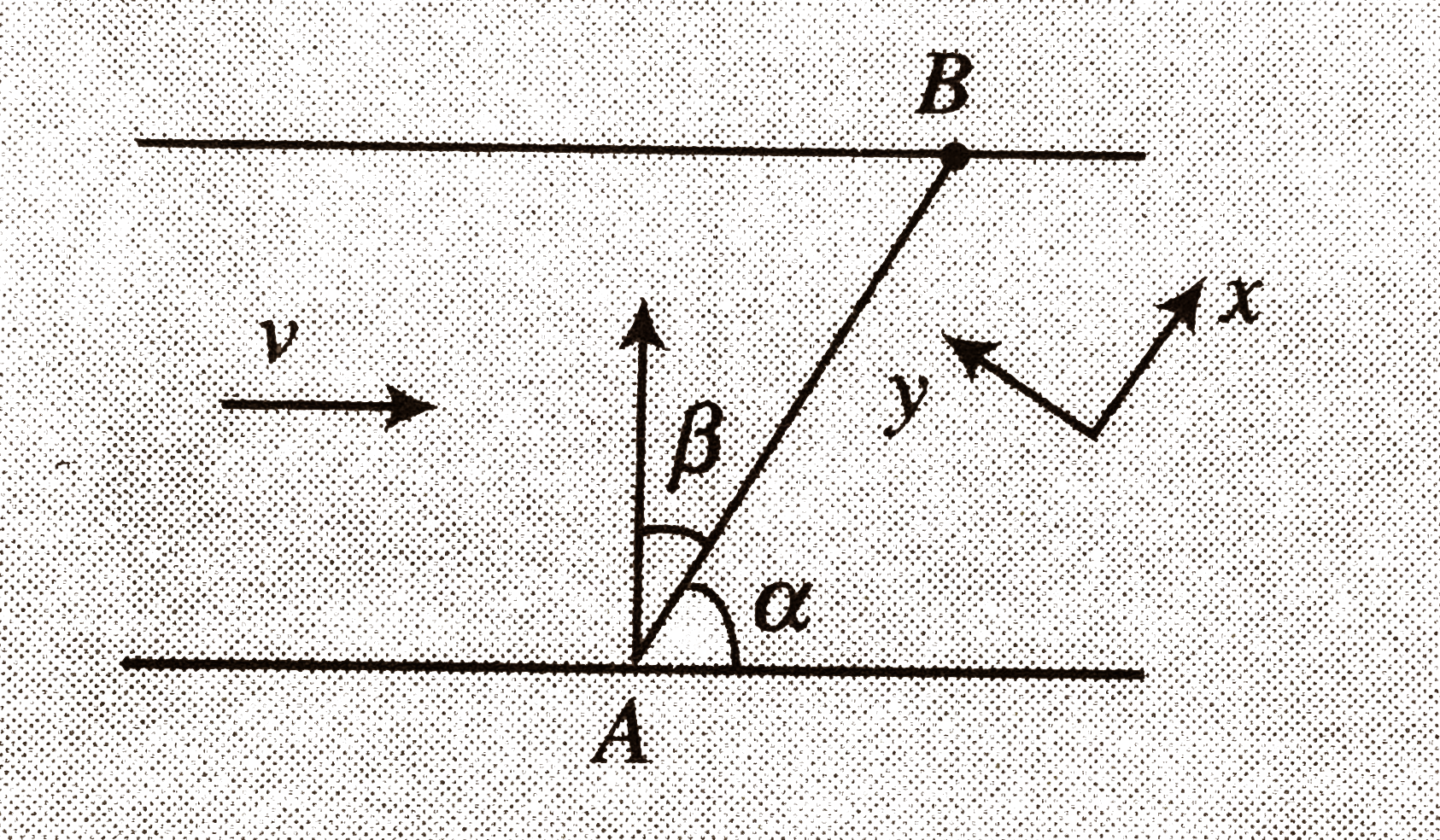 .
.
View SolutionA steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?
View Solution
Knowledge Check
A man wishes to cross a river to an exactly opposite point on the other bank. if the can swim with twice the velocity of the current, the inclination to the current of the direction he should swim is
A30∘B45∘C60∘D120∘A person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
A9.4B2C84.6D28.2
A steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?
View SolutionTwo trees, A and B are on the same side of a river. From a point C in the river the distance of trees A and B are 25 m and 300 m respectively. If the angle C is 450 , find the distance between the trees (use √2=1.44)
View SolutionA bridge across the river makes an angle of 30∘ with the river bank. If the length of the bridge across the river is 60m, Find the width of the river.
View SolutionA bridge in the shape of straight path across a river, makes an angle of 60∘ with the width of the river. If the length of the bridge is 100m, then find the width of the river.
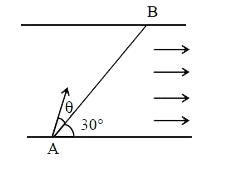
View SolutionA swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
View SolutionTwo trees A and B are on the same side of a river. From a point C in the river, the river, the distance of trees A and B are 250 m and 300 m and respectively. If angle of C=45^0. find the distance between trees.
View Solution
