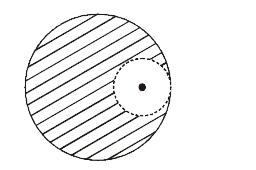
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)

−2GM3R
−2GMR
−GM2R
−GMR
The correct Answer is:D
(d) Due to complete solid sphere, potential at point P
Vsphere=−GM2R3[(3R2−(R2)2))]
−Gm2R3(11R24)=−11kGM8R

Due to cavity part potential at point P
Vcavity=−328R/(2)=−3GM8R
So potential at the centre of cavity
=Vsphere−Vcavity=−11GM8R−(−38GMR)=−GMR
Topper's Solved these Questions
Similar Questions
From a solid sphere of mass M and radius R, a spherical portion of radiu R2 is removed as shown in the figure. Taking gravitational potential V = 0 at r=∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)
View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View Solution
Knowledge Check
A shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A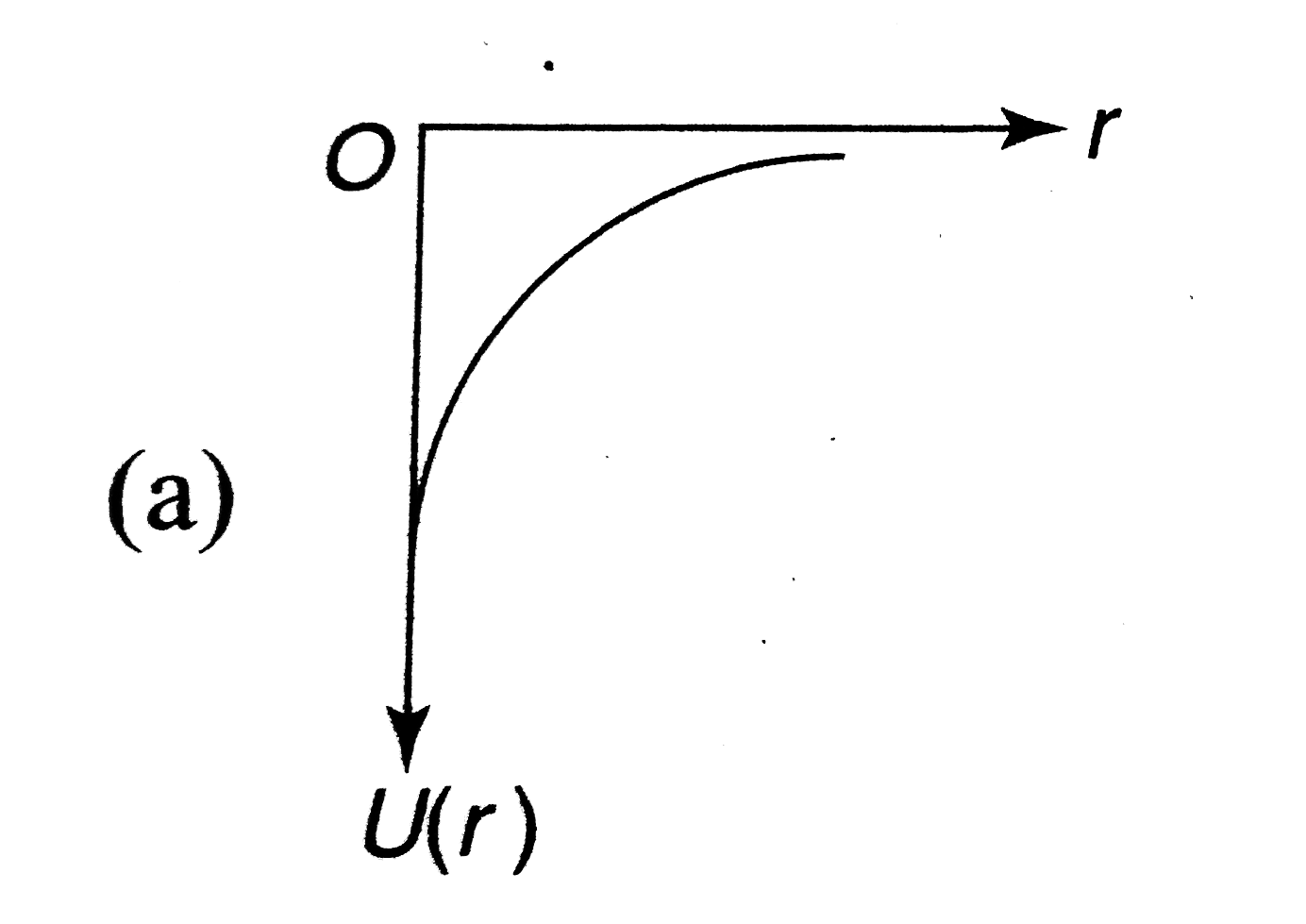 B
B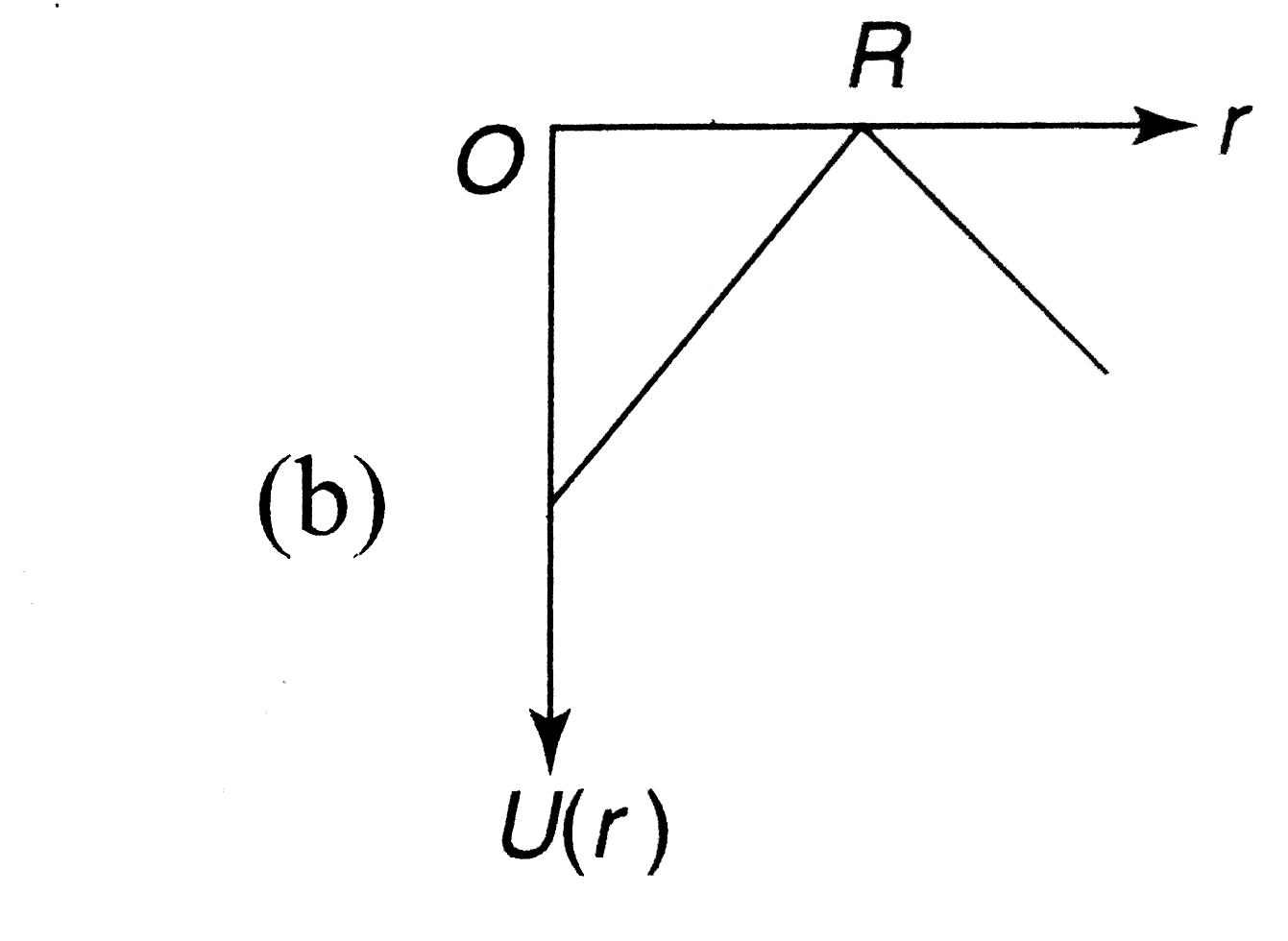 C
C D
D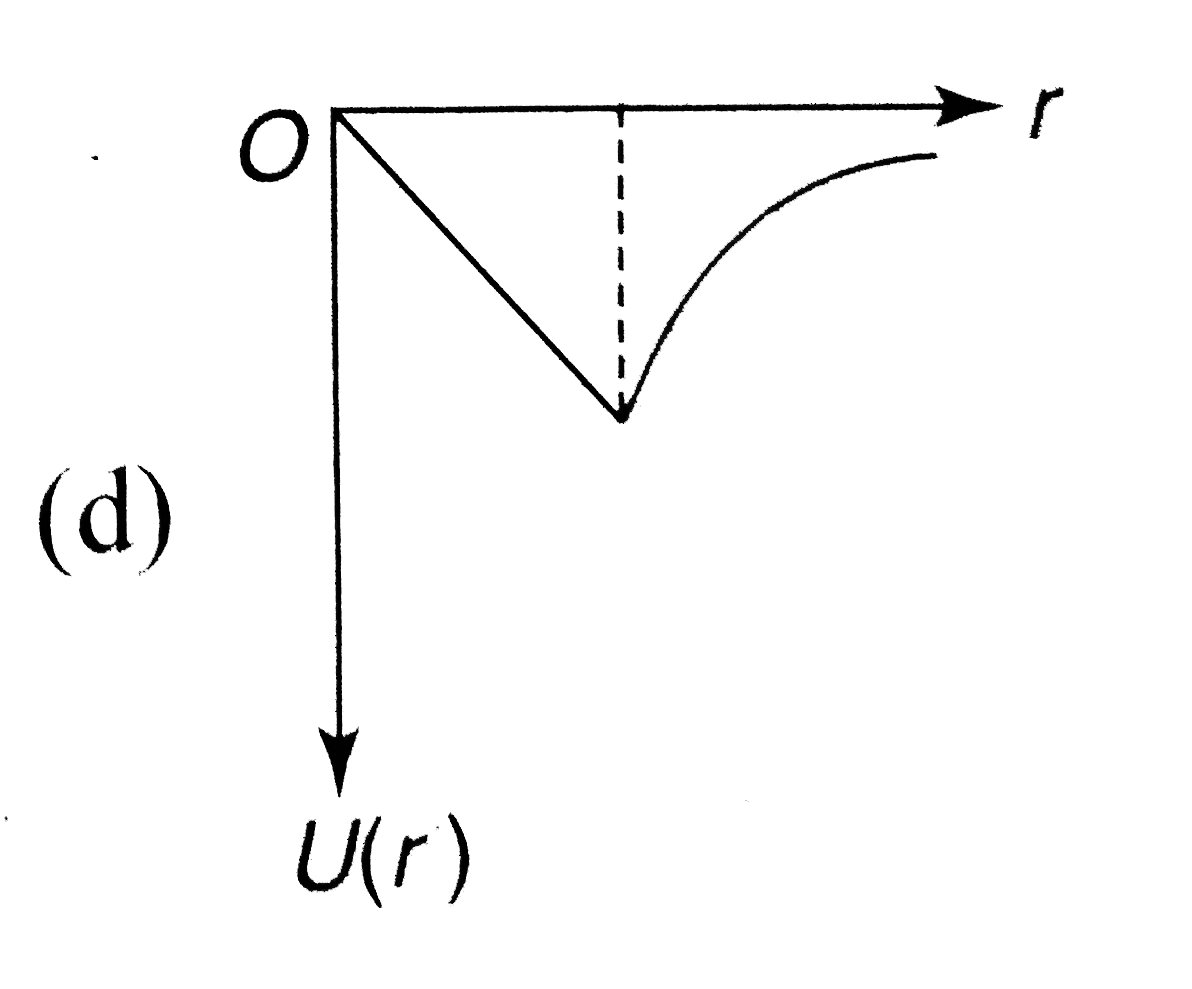
A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
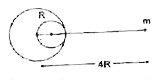
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionThree solid spheres of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
View Solution
