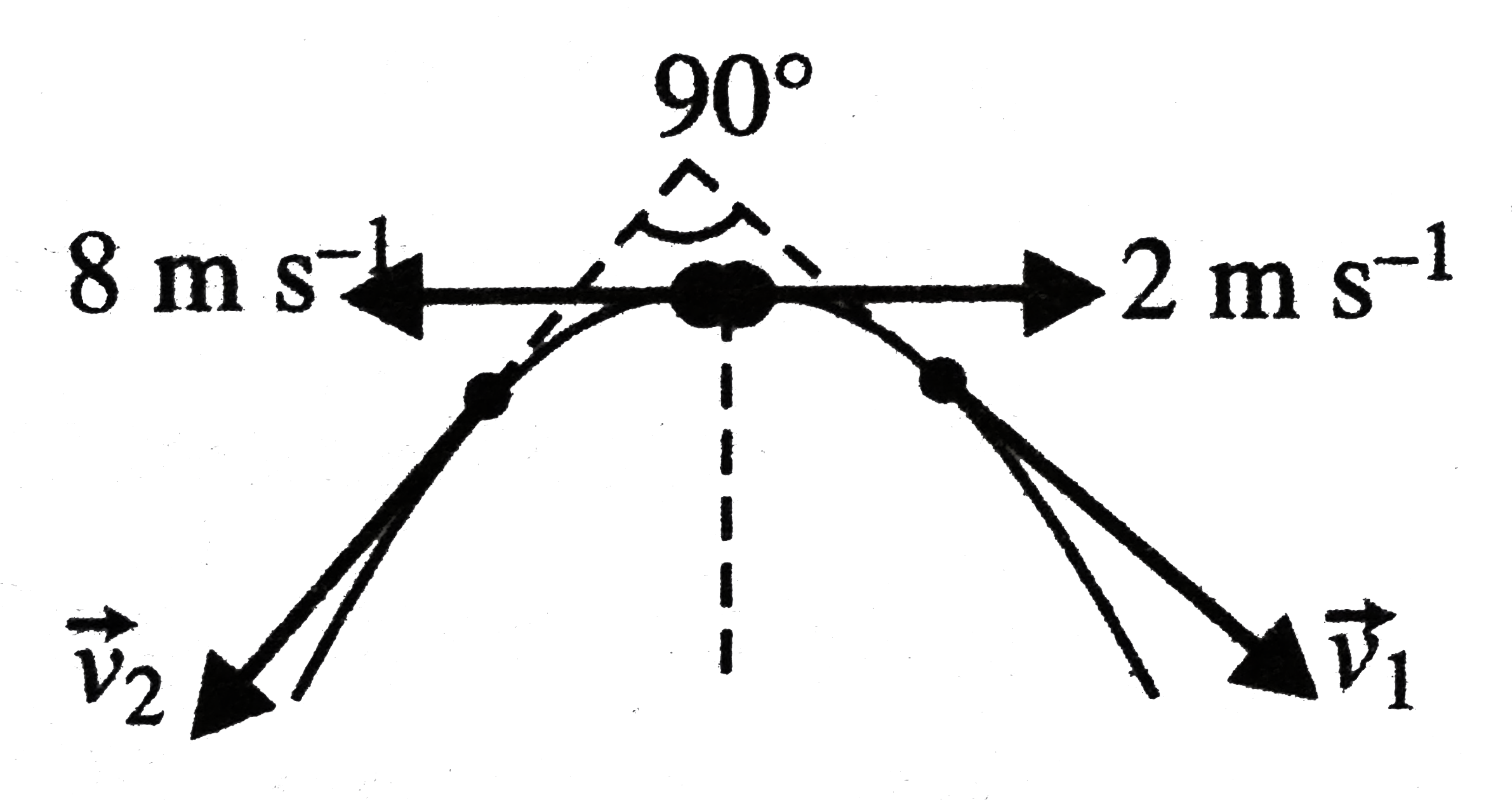
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the velocity vectors of two bodies to become perpendicular to each other is :
0.1 s
0.2 s
0.4 s
0.8 s
The correct Answer is:C
(c) Velocity of first body at any instant t, →v1=2ˆi−gtˆj
Velocity of second body at any instant
→v2=−8ˆi−gtˆj
Since →v1⊥→v2,i.e.,→v1.→v2=0
(2ˆi−gtˆj).(−8ˆi−gtˆj)=0⇒−16+g2t2=0
⇒t=√16g2⇒t=410=0.4s
→S1=(2×0.4)ˆi,→S2=(8×0.4)(−ˆi)
→S1=0.8ˆiand→S2=−3.2ˆi
Separation =→S1−(−→S2)=0.8ˆi+(3.2ˆi)=4ˆi
→S1=2tˆi−12gt2ˆj,→S2=−8tˆi−12gt2ˆj
As →S1⊥→S2,i.e.,→S1.→S2=0
−16t+12×12g2t2=0⇒g2t2=16×4
⇒>=4×2⇒t=810=0.8s.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Two particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View Solution
Knowledge Check
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.A0.1 sB0.2 sC0.8 sD0.6 sFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.A1 mB0.5 mC2 mD4 mTwo trains, each 50m long, are travelling in opposite directions with velocities 10ms−1and15ms−1. The time of their crossing each other is.
A2 sB4 sC2√3D4√3
From the top of the tower, two balls are thrown horizontally in opposite directions with velocities u1 and u2. Find the distacne between the balls at the moment when their velocity vectors becomes mutually perpendicular. (Assume the height of tower very large)
View SolutionFrom the top of tower of height 80m, two stones are projected horizontally with velocities 20ms−1 and 30ms−1 in opposite directions, Find the distance between both the stones on reaching the ground (in102m).
View SolutionFrom an elevated point two bodies are projected horizontally in opposite direction with velocity "10m/s" each.Time after which their displacements are perpendicular to each other isg=10ms2
View SolutionFrom the top of a tower of height H, identical bodies,A and B ,are thrown horizontally with velocities 100ms−1 and 50ms−1 in the same direction at the same instant. Then
View SolutionTwo trains 110m and 90m log respectively, are trunning in opposite directions with velocities 36kmh−1 and 54kmh−1 Find the time taken by the trains to completely cross each other.
View Solution
