From an inclined plane a particleis thrown in a direction normal to the surface. Find the ratio of successive ranges of the particle on inclined plane. Consider all collisions as elastic collisions (particle rebounds with the same speed with which it strikes the plane)
The correct Answer is:[1:3:5]
Step by step video, text & image solution for From an inclined plane a particleis thrown in a direction normal to the surface. Find the ratio of successive ranges of the particle on inclined plane. Consider all collisions as elastic collisions (particle rebounds with the same speed with which it strikes the plane) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question
18 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct
35 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
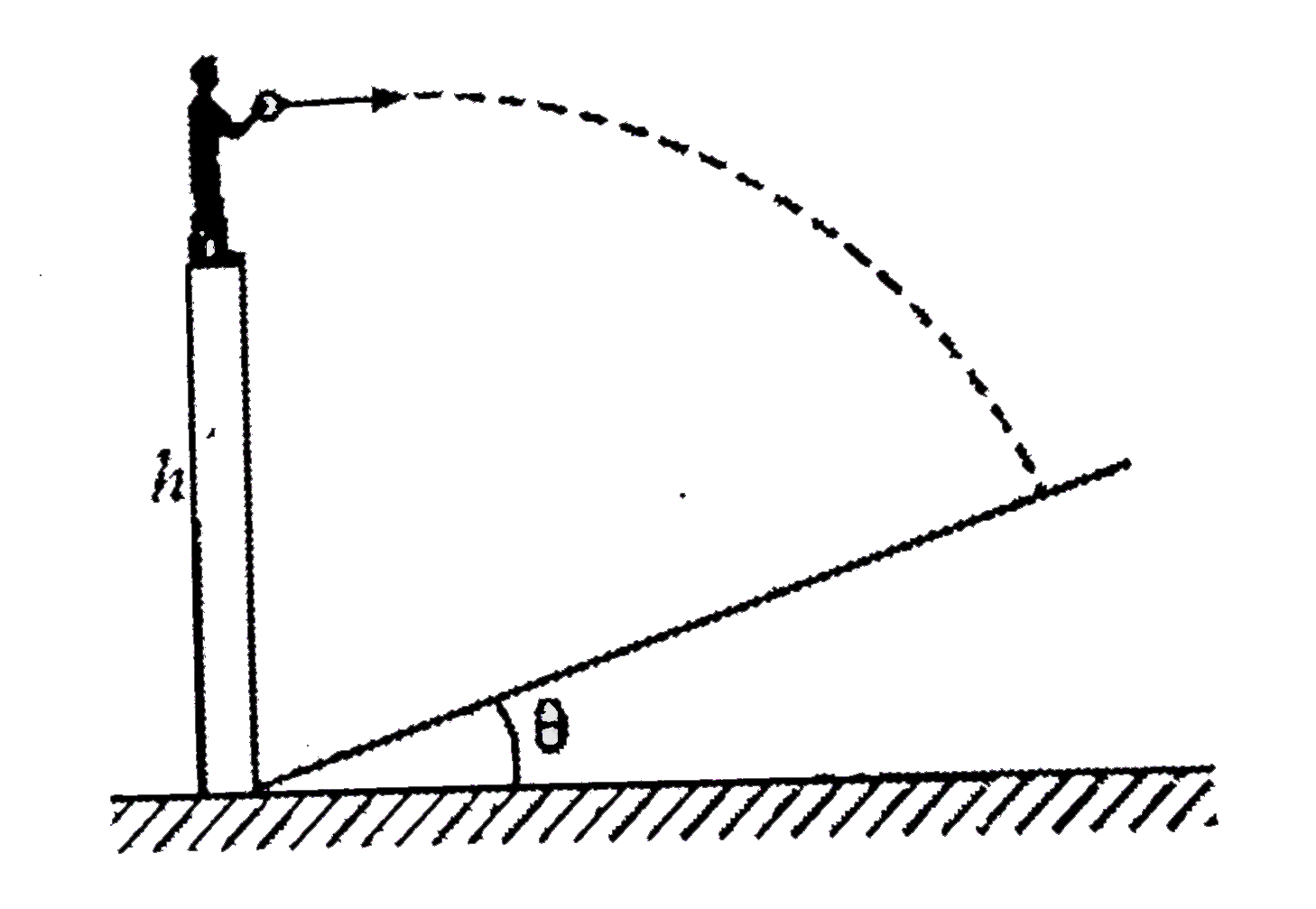
A partacle is thrown in horizontal direction with speed u from a point P, the top of a tower shown in figure.1.49 at a vertical height h above the inclined plane of inclination θ. Find the speed with which the particle is thrown so that it strikes the plane normally. Also find the distance from the foot of the tower where the particle will strike.
View SolutionA particle of mass m strikes another particle of same at rest. Find the angle between velocities of particles after the collision , if the collision is elastic.
View Solution
Knowledge Check
The ratio of the range of the particle and its maximum range in the inclined plane is:
A1:2B1:√2C1:√3D1:1A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gTwo balls are thrown from an inclined plane at angle of projection with the plane, one up the incline and the other down the incline as shown. Which one is not correct?
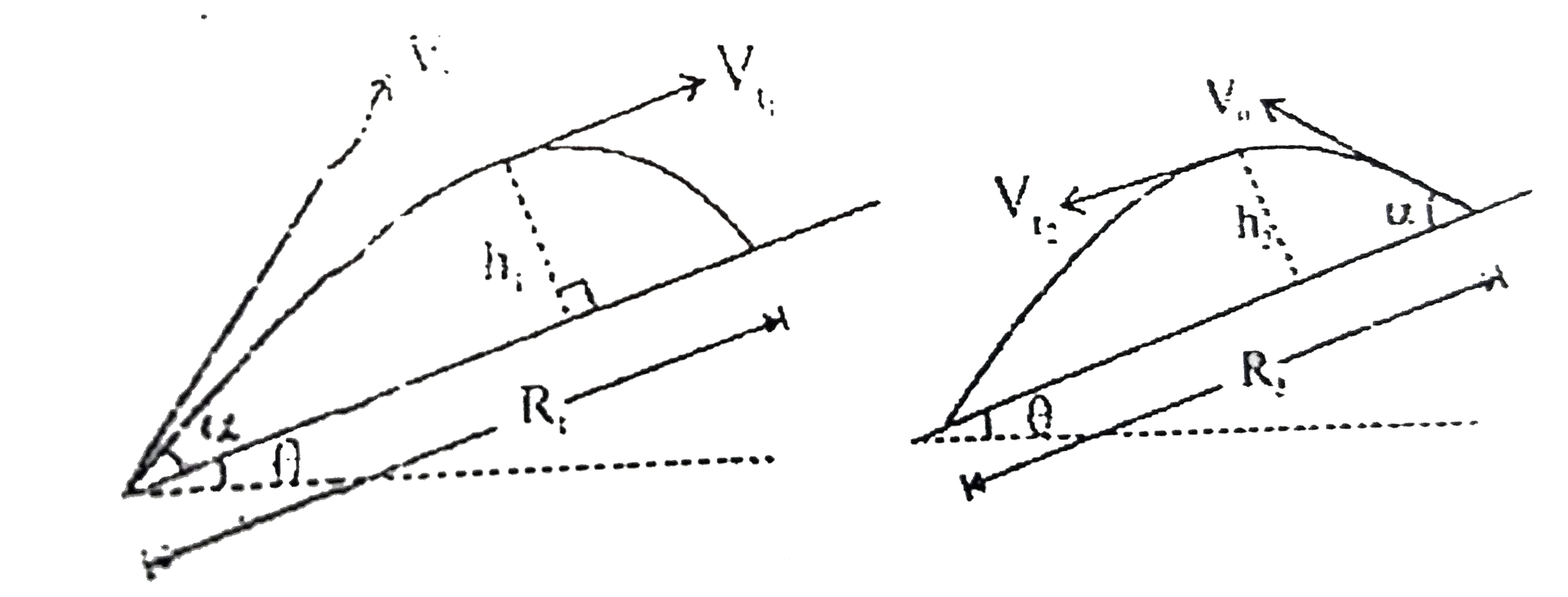 Ah1−h2=v20sin2α2gcosθBT1=T2=2v0sinαgcosθCR2>R1Dvt1=vt2
Ah1−h2=v20sin2α2gcosθBT1=T2=2v0sinαgcosθCR2>R1Dvt1=vt2
A particle of mass m1 moving on a smooth surface with some velocity strikes another particle of mass m2 at rest. The head - on elastic collision takes place. After the collision , particles move with equal speed in opposite direction . Determine the mass ratio.
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to nthe horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. u
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. h
View SolutionTwo particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View Solution
