Given figure shows a massless platform kept on a light elastic spring attached to ground from one end .
A small particle of mass 0.2 kg is dropped on the paltform from a height of 0.26 m , which causes a compression of 0.01 m in the spring . Calculate the height from which the particle must be dropped in order to cause a compressin of 0.05 m .
To solve the problem, we need to apply the principle of conservation of energy. The potential energy lost by the particle when it is dropped from a height will be equal to the potential energy gained by the spring when it is compressed.
1. Identify Given Values:
- Mass of the particle, m=0.2kg
- Initial height from which the particle is dropped, h=0.26m
- Compression of the spring when dropped from height h, x=0.01m
- New compression of the spring we want to achieve, x1=0.05m
2. Apply Conservation of Energy:
The potential energy lost by the particle when it falls is equal to the potential energy stored in the spring when it is compressed.
Potential Energy lost=Potential Energy gained by spring
This can be expressed as:
mgh+mgx=12kx2
Where k is the spring constant.
3. Set Up the Equations:
For the first case (compression x=0.01):
mg(0.26)+mg(0.01)=12k(0.01)2(1)
For the second case (compression x1=0.05):
Let the new height be h1:
mg(h1)+mg(0.05)=12k(0.05)2(2)
4. Divide the Two Equations:
Dividing equation (1) by equation (2):
mg(0.26+0.01)mg(h1+0.05)=12k(0.01)212k(0.05)2
The mg and 12k terms cancel out:
0.26+0.01h1+0.05=(0.010.05)2
5. Simplify the Equation:
The right-hand side simplifies to:
(0.010.05)2=(15)2=125
Thus, we have:
0.27h1+0.05=125
6. Cross-Multiply and Solve for h1:
Cross-multiplying gives:
0.27⋅25=h1+0.05
6.75=h1+0.05
h1=6.75−0.05=6.70m
Final Result:
The height from which the particle must be dropped to cause a compression of 0.05m in the spring is:
6.70m
- Mass of the particle, m=0.2kg
- Initial height from which the particle is dropped, h=0.26m
- Compression of the spring when dropped from height h, x=0.01m
- New compression of the spring we want to achieve, x1=0.05m
The potential energy lost by the particle when it falls is equal to the potential energy stored in the spring when it is compressed.
Potential Energy lost=Potential Energy gained by spring
This can be expressed as:
mgh+mgx=12kx2
Where k is the spring constant.
For the first case (compression x=0.01):
mg(0.26)+mg(0.01)=12k(0.01)2(1)
Let the new height be h1:
mg(h1)+mg(0.05)=12k(0.05)2(2)
Dividing equation (1) by equation (2):
mg(0.26+0.01)mg(h1+0.05)=12k(0.01)212k(0.05)2
The mg and 12k terms cancel out:
0.26+0.01h1+0.05=(0.010.05)2
The right-hand side simplifies to:
(0.010.05)2=(15)2=125
Thus, we have:
0.27h1+0.05=125
Cross-multiplying gives:
0.27⋅25=h1+0.05
6.75=h1+0.05
h1=6.75−0.05=6.70m
The height from which the particle must be dropped to cause a compression of 0.05m in the spring is:
6.70m
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - PRACTICE PROBLEMS
27 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions
20 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
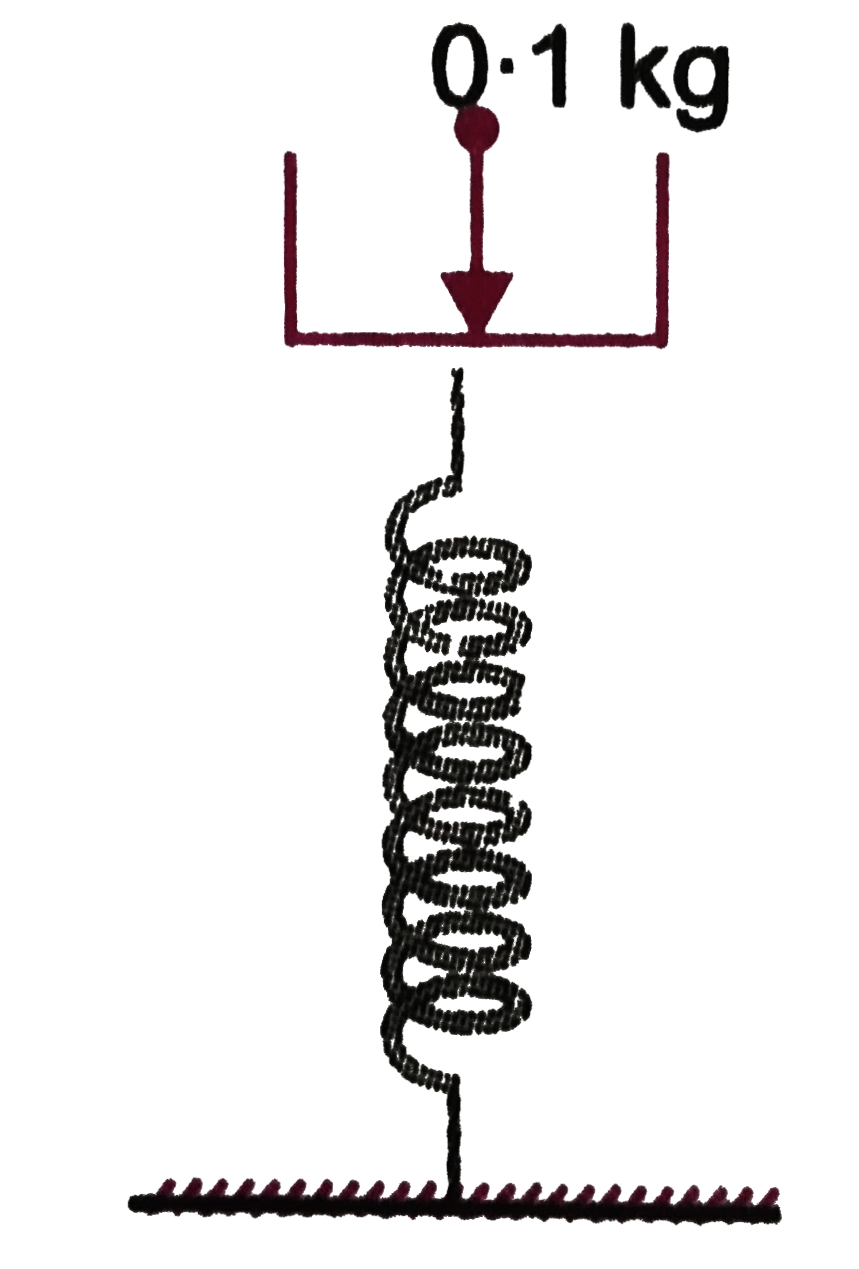
View SolutionA platform having no mass is kept on a light elastic spring . When a small particle of 0.1 kg is dropped on this spring from a height of 0.50 m , the spring is compressed by 0.02 m . From which height the particle should be dropped to produce a compression of 0.05 m ?
View Solution
Knowledge Check
A massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
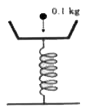 A0.96 mB2.96 mC3.96 mD0.48 m
A0.96 mB2.96 mC3.96 mD0.48 m
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionThe two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be

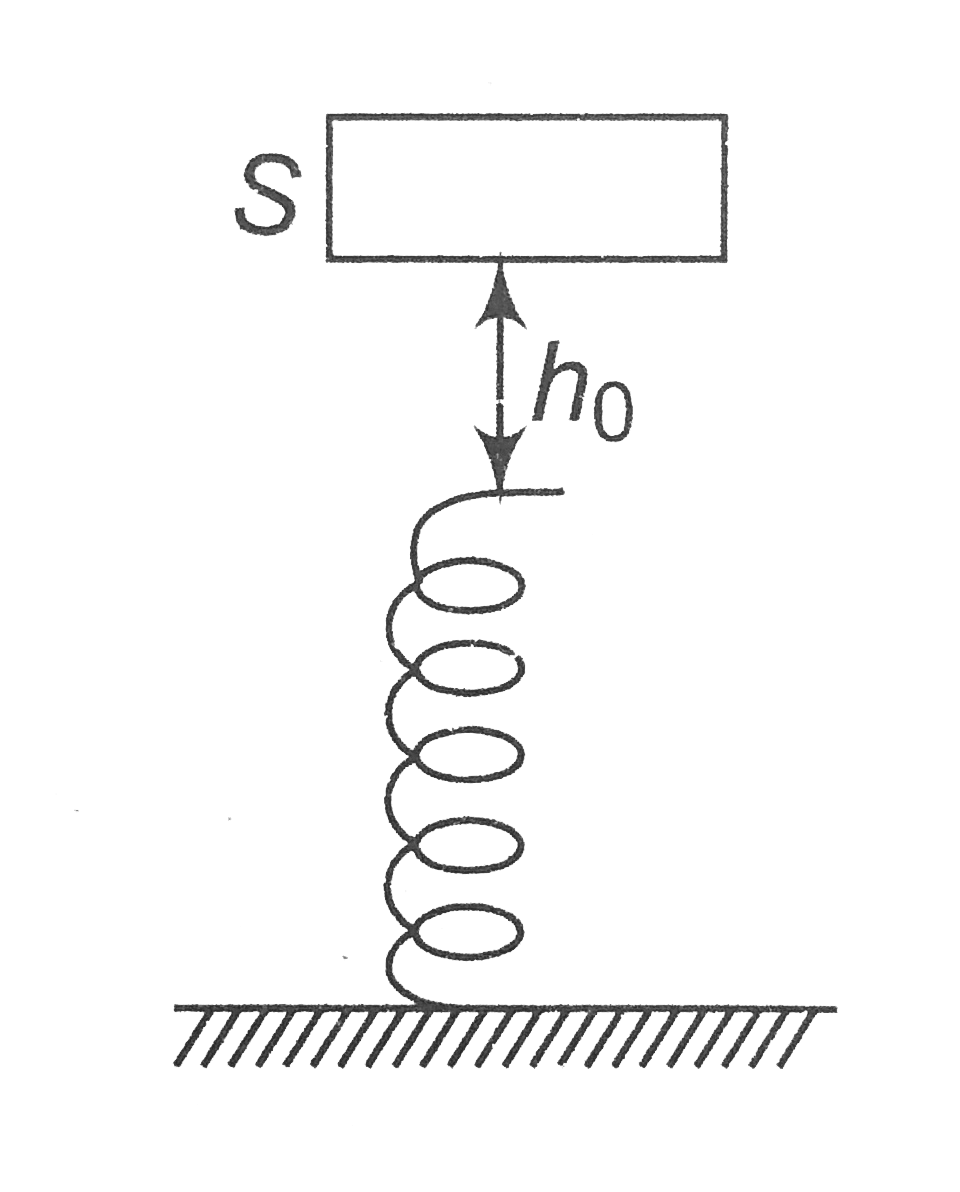
View SolutionA slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
View Solution
