Given k1=1500Nm−1, k2=500Nm−1, m1=2kg, m2=1kg. Find:

a. potential energy stored in the spring in equilibrium, and
b. work done in slowly pulling down m2 by 8cm.
The correct Answer is:a. 0.4J; b 1J;
Let the initial extension in the springs of force constants k1 and k2, at equilibrium position, be x1 and x2. Then
x2=m2gk2, x1=(m1+m2)gk1

a. Potential energy stored in the springs in equilibrium position is
U1=12k1x21+12k2x22
Putting values of x1 and x2 from above, we get U1=0.4J
b. Let Δx1 and Δx2 be additional elongations caused by pulling m2 by l=8cm. Additional forces on m1 are equal and in opposite directions.
⇒k1Δx1=k2Δx2 (i)
Also, Δx1+Δx2=l (ii)
Δx1 and Δx2 can be found from Eqs. (i) and (ii).
From work-energy theorem,
wg+wp+ws=0
(where wp is the work done by the pulling force)
⇒wp=−ws−wg=(U2−U1)−[m1gΔx1+m2g(Δx1+Δx2)]
where U2=12k1(x1+Δx1)2+12k2(x2+Δx2)2
Putting the values, we get
⇒wp=1J
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The tension in the string connected between blocks is

View SolutionIn figure m1=5kg,m2=2kgandF=1N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.

View Solution
In an elevator a system is arranged as shown in figure. Initially elevator is at rest and the system is in equilibrium with middle spring unstretched. When the elevator accelerated upwards, it was found that for the new equilibrium position (with respect to lift), the further extension i the top spring is 1.5 times that of the further compression in the bottom spring, irrespective of the value of acceleration
(a) Find the value of m1m2 in terms of spring constants for this happen.
(b) if k1=k2=k3=500Nm and m1=2 kg and acceleration of the elevator is 2.5ms2, find the tension in the middle spring in the final equilibrium with respect to lift.
View SolutionIn the problem if k = 10 N/m, m=2kg, R=1m and A=2m. Find linear speed of the disc at mean position.

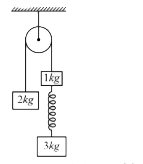
View SolutionFrom the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
View SolutionTwo springs with negligible massess and force constant of k1=200Nm−1 and k2=160Nm−1 are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position ir. Which both springs are neither stretched nor compressed. At time t = 0, sharp impulse of 50 N-s is given to the block in horizontal direction.
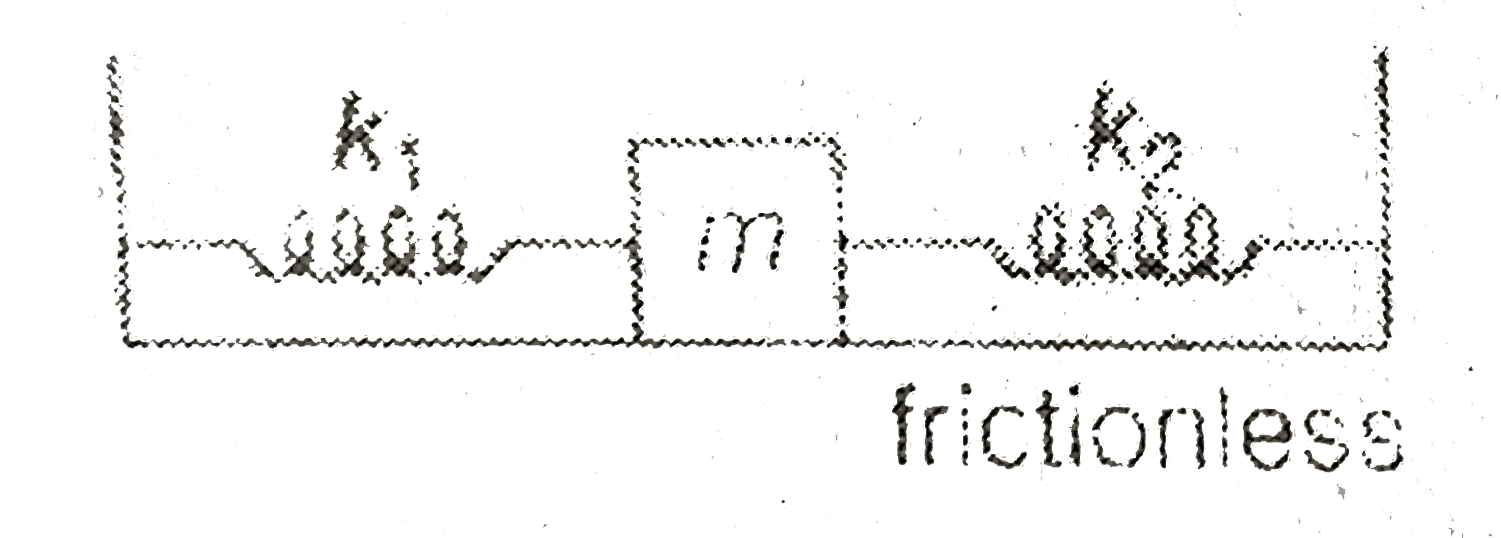
View SolutionForce constants K1andK2 of two springs are in the ratio 5:4. They are stretched by same length. If potential energy stored in one spring is 25 J then potential energy stored in second spring is
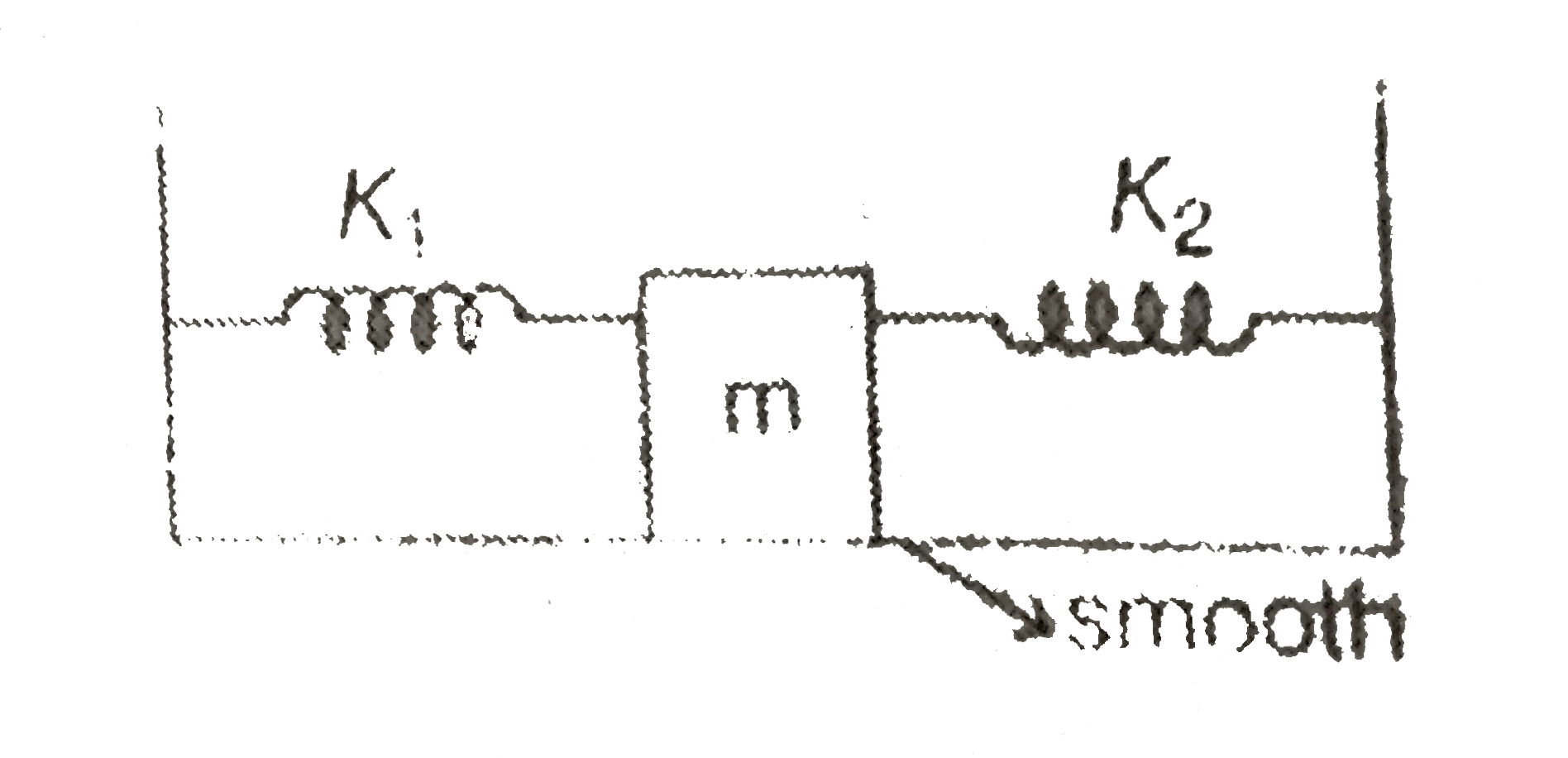
View SolutionTwo springs with negligible massess and force constant of k1=200Nm−1 and k2=160Nm−1 are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position nor compressed. At time t=0, sharp impulse of 50 N-s is given to the block.
View SolutionA body of mass 1 kg is rotated in a horizontal circle of radius 1 m and moves with velocity 2ms−1 The work done in 10 revolutions is
View SolutionDetermine the energy stored in the surface of. a soap bubble of radius 2.1 cm if its tension is 4.5×10−2Nm−1
View Solution