From the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
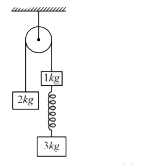
(a)10 cm
(b)20 cm
(c)30 cm
(d)25 cm
The correct Answer is:B
T - 20 = 20….(i) 10 + kx - T = a …(2) 30 - kx = 3a …..(3)
Adding all the equation 10 + 30 - 20 a ⇒103m/s2
⇒x=30−3ak=30−3×103100=20100n
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Main (Archive) Level - I29videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 175videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
From the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if k=100N/m. (Neglect oscillations due to spring)
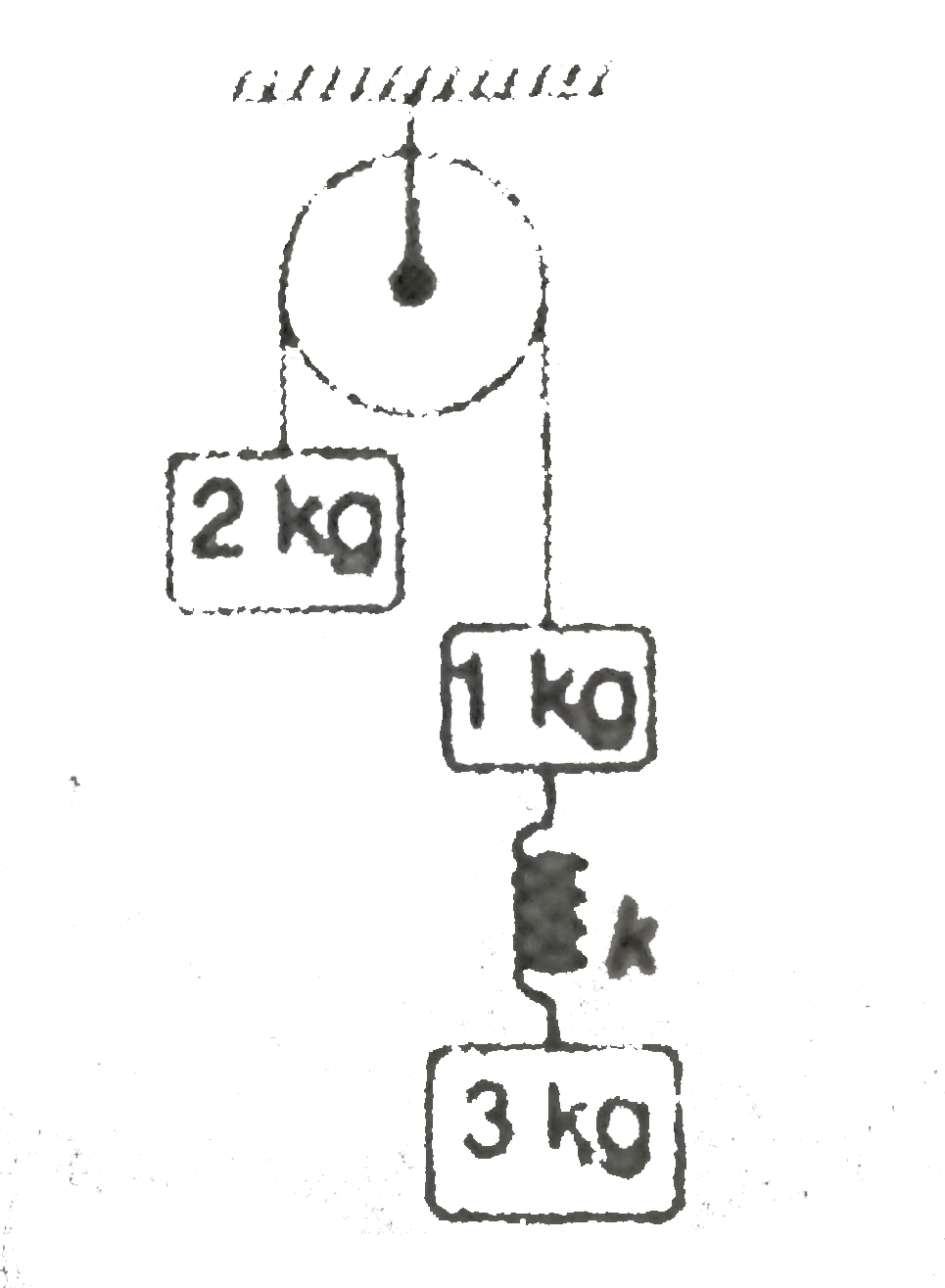 View Solution
View SolutionTwo block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
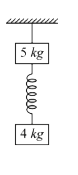 View Solution
View SolutionFind the acceleration of 3kg mass when acceleration of 2kg mass is ms−2 as shwon in fig.
 View Solution
View SolutionFind the acceleration of 3 kg mass when acceleration of 2 kg mass is 2ms−2 as shown in figure-2.140
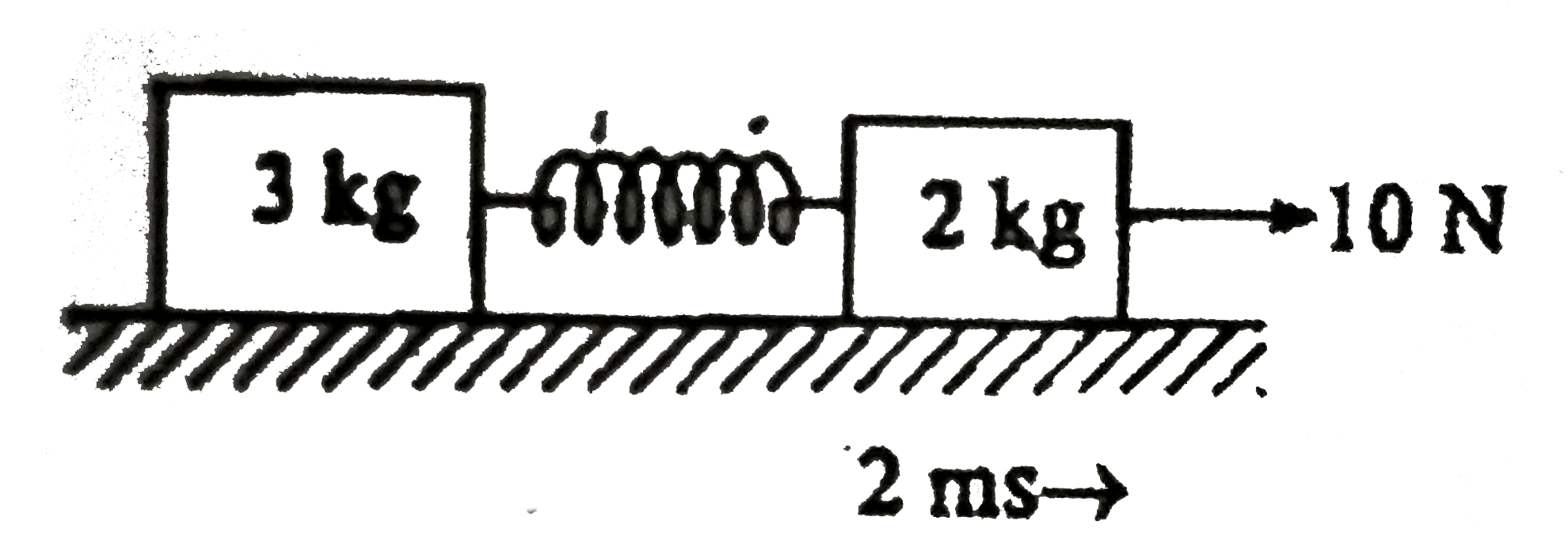 View Solution
View SolutionIn figure shown if 2 kg block is moving at an acceleration 2m/s2, find the elongationin spring and acceleration of 4 kg block at this instant. Take g= 10m/s2.
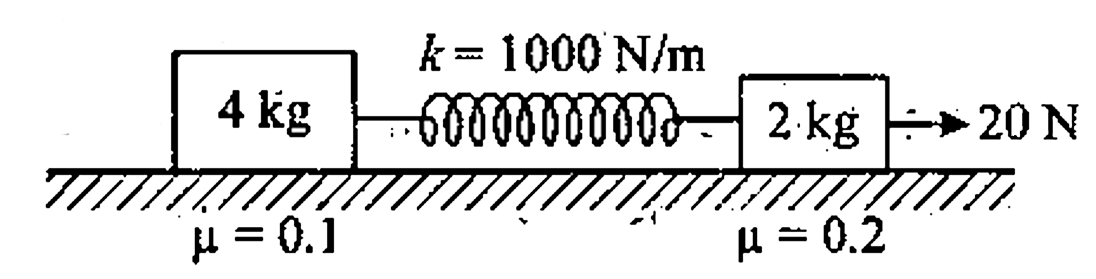
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
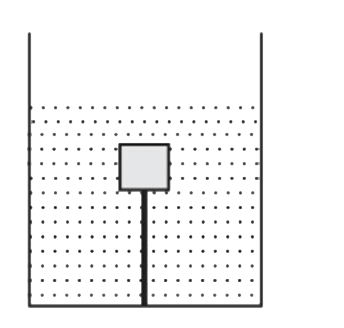 View Solution
View SolutionA point mass m = 20 kg, is suspended by a massless spring of constant 2000 N/M. The point mass is released when elongation in the spring is 15 cm. The equation of displacement of particle as a function of time is ( Take g=10m/s2 )
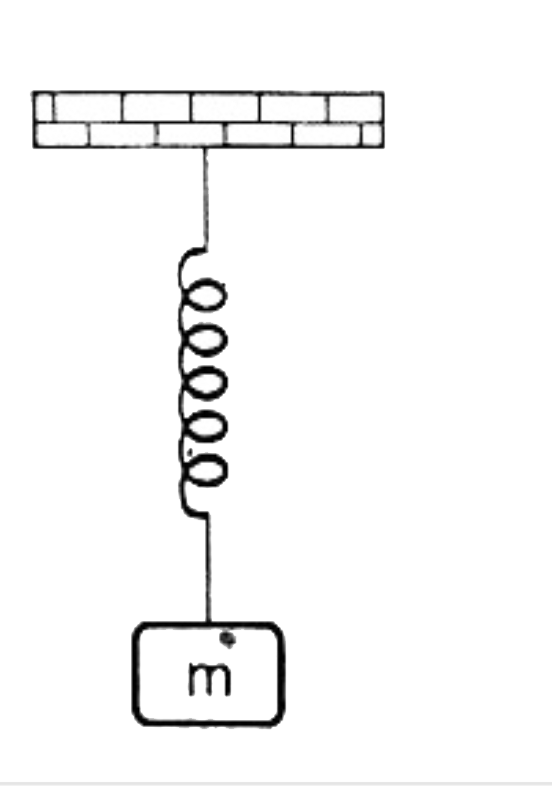 View Solution
View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of 5kg block when 2kg block leaves the constant of with ground is (force constant of spring k=40N/mandg=10m/s2)
 View Solution
View SolutionTwo masses as shown are suspended from a massless pulley. Calculate the acceleration of the 10 kg mass when masses are left free
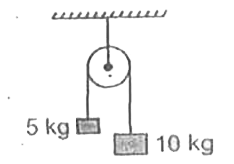 View Solution
View SolutionTwo masses 5 kg and 3 kg are suspended from the ends of an unstretchable light string passing over a frictionless pulley. When the masses are released, the thrust on the pulley is (g = 10ms−2)
View Solution

