Given →F=(xy2)ˆi+(x2y)ˆjN. The work done by →F when a particle is taken along the semicircular path OAB where the coordinates of B are (4,0) is
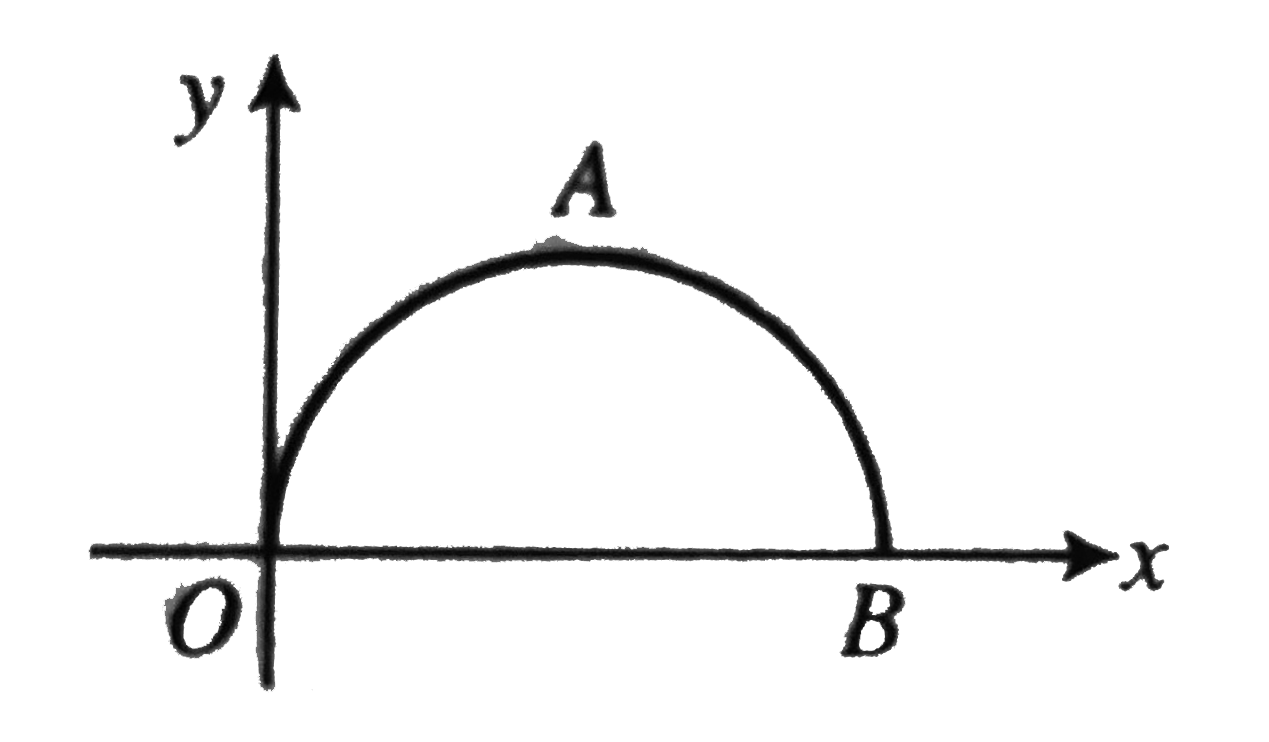
(a) 653J
(b) 752J
(c) 734J
(d) Zero
The correct Answer is:D
Given →F=(xy)2ˆi(x2y)ˆj
W=∫Fxdx+∫Fydy
=∫xy2dx+∫x2ydy
=12∫d(x2y2)=[x2y22]4,00,0=0
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Force acting on a pasrticle is →F=(αyˆi+βxyˆj). Find the work done by this force, when pasrticle is moved alolng the line 2x=3y from origin to the point (3,2) {take quantities in SI units and α=1,β=1}
View SolutionA force acting on a particle moving in the x-y plane is given by →F=(2yˆi+x2ˆj)N, where x and y are in meters. The particle moves from the origin to a final position having coordinates x=5.00m as shown in figure. Calculate the work done by →F on the particle as it moves along (a) OAC, (b) OBC, and (c) OC. (d) Is →F conservative or non-conservative? Explain.
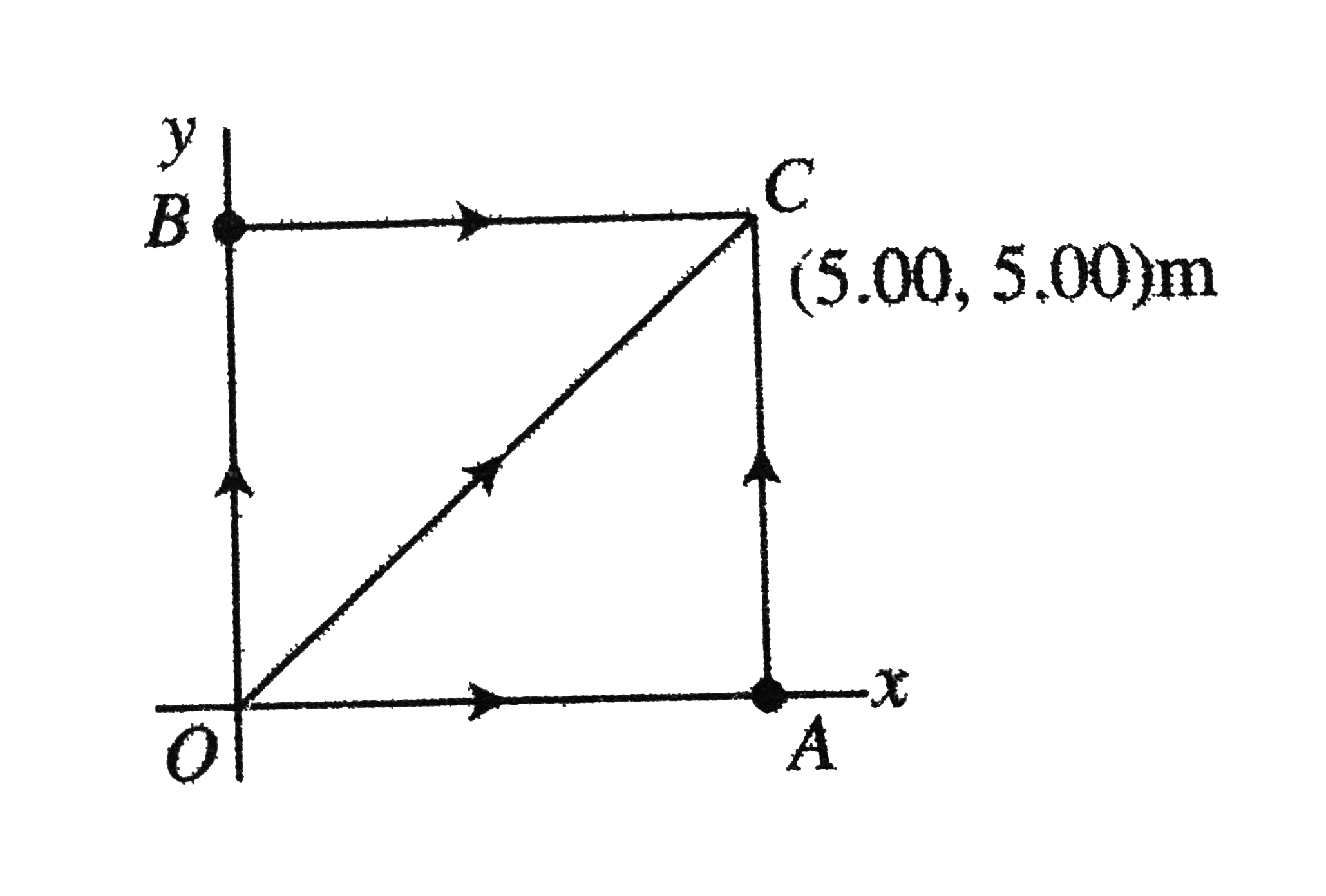
View SolutionA force →F=(3ˆi+4ˆj) N is acting on a particle. Work done by the force is zero, when particle is moving on the line 2y+Px=2, the value of P is
View SolutionThe work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
View SolutionA force →F=(3xN)ˆi+(4N)ˆj, with x in meter, acts on a particle, changing only the kinetic energy of the particle. How mcuh work is done on the particle as it moves from coordinates (2m,3m,5m) to (3m,0m,6m)? Does the speed of the particle increase, decrease, or remain the same?
View SolutionA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
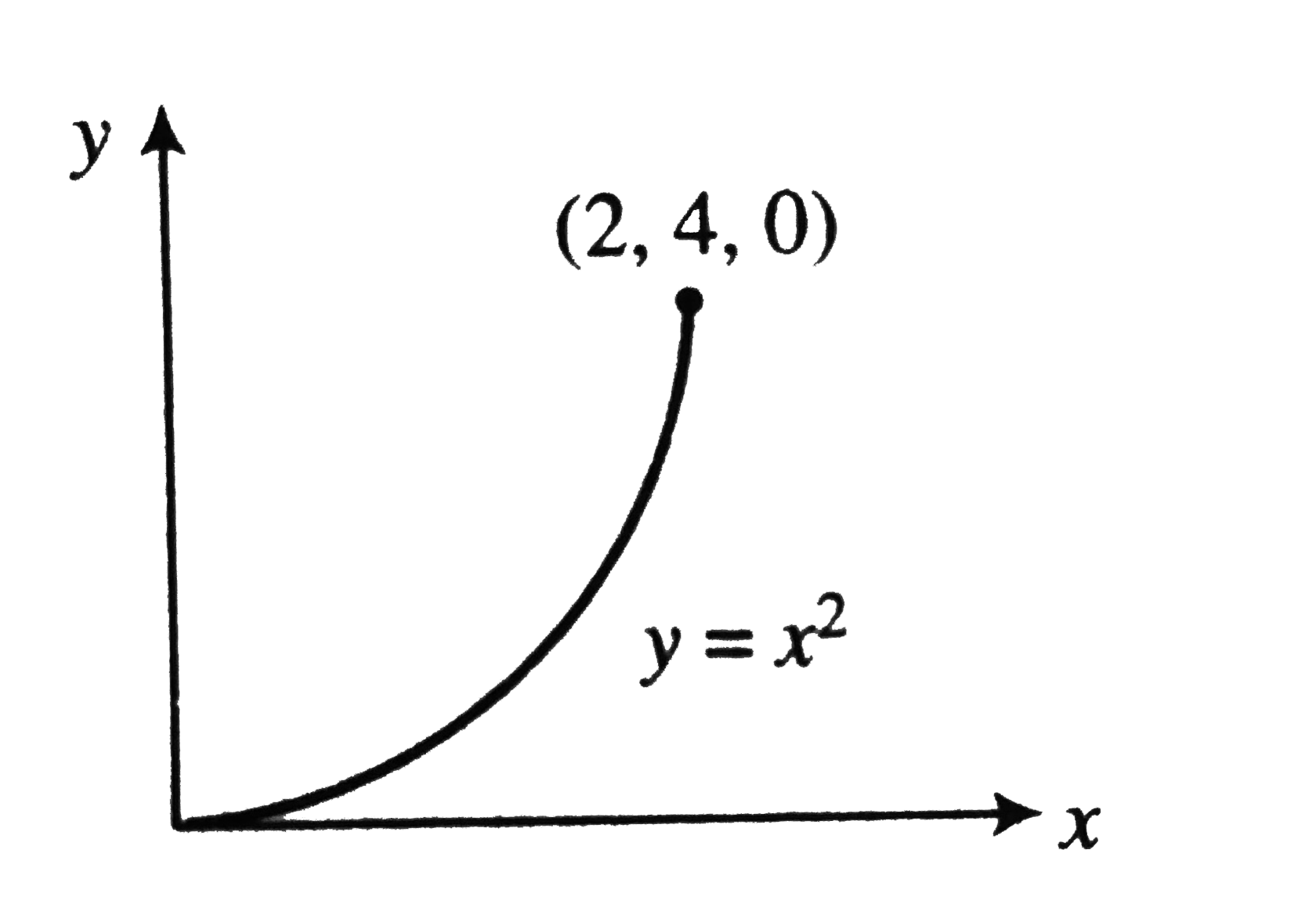
View SolutionA particle moves in x-y plane under action of a path dependent force F=yˆi+xˆj. The work done by the force as it moves in x-y plane can be evaluated by solving the integral ∫→F.→dr,where →dr=dxˆi+dyˆj. The position coordinates x and y will vary according to some constraint determined by teh path followed by the particle. For example, if particle moves along a straight line from one position to other, then an possible rarticle. For example, if particle moves along a straight line from one position to other, then a possible relation is y=mx+c. NOw. try to solve the following questions.
1. The particel moves along a straight line from origin to (a ,a) . The work done by the force on the particle is
(1)a2 (2)2s (3)a22 (4)Zero
2. The particle moves from (0,0) to (a,0) and then from, (a,0) to (a,a), in straight line paths. The work done by the force on the particle is
(1)a2 (2)2a (3)a22 (4) Zero
3. The differential work by the given force over an elementary displacement is given as dW=→F.→dr=ydx+xdy
This can be expressed as dW=d(xy). From this, it can be inferred that the work done by the force
(1) Depends only on initial and final values of x and y
(2) Depends on initial and final values and on the path followed
(3) Is zero for any values of x and y
(4) Is zero when object returns to original position after following any path
View SolutionA body is subjected to a constant force given by
→F(N)=−ˆi+2ˆj+3ˆk
What is the work done by this force in moving the body through a distance of 4 m along the z=axis and then 3 m along the y-axis?
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
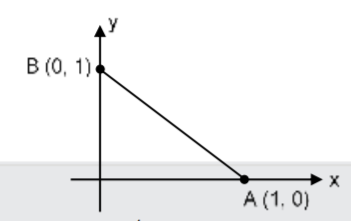
View SolutionA force given by →F=fxˆi+fyˆj+fzˆk acts on a particle which moves from (a, b, c) to (d, e, f). The work done by the force F is : (Here A1,A2,A3 are magntitude of area bounded )
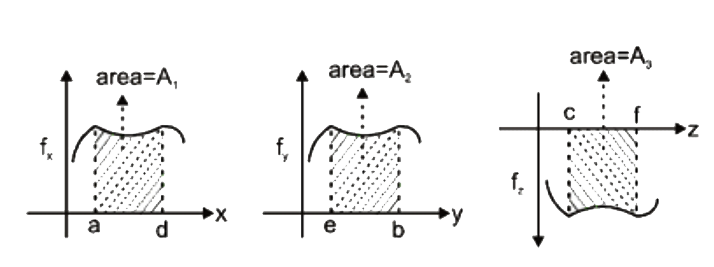
View Solution
