Gravitational field due to a solid sphere
remains constant throughout the sphere
increase inside the sphere and decreases outside the sphere
increases throughout with distance from the center
decreases throughout with distance from the centre
The correct Answer is:B
To find the gravitational field due to a solid sphere, we can analyze the behavior of the gravitational field both inside and outside the sphere.
1. Understanding Gravitational Field:
The gravitational field (E) at a distance r from the center of a solid sphere is influenced by the mass of the sphere (M) and the distance from its center.
2. Gravitational Field Inside the Sphere:
For a point inside a solid sphere (where r < R, R being the radius of the sphere), the gravitational field is given by:
Er=G⋅Mrr2
where Mr is the mass enclosed within radius r. According to Gauss's law for gravitation, the mass enclosed within a radius r is proportional to the volume of the sphere of radius r:
Mr=MR3⋅r3
Therefore, the gravitational field inside the sphere becomes:
Er=G⋅(MR3⋅r3)r2=G⋅MR3⋅r
This shows that the gravitational field inside the sphere increases linearly with r.
3. Gravitational Field Outside the Sphere:
For a point outside the solid sphere (where r > R), the gravitational field is given by:
Er=G⋅Mr2
This indicates that the gravitational field outside the sphere decreases with the square of the distance from the center of the sphere.
4. Conclusion:
- Inside the sphere, the gravitational field increases linearly with distance from the center.
- Outside the sphere, the gravitational field decreases with the square of the distance from the center.
Thus, the correct option is that the gravitational field increases inside the sphere and decreases outside the sphere.
The gravitational field (E) at a distance r from the center of a solid sphere is influenced by the mass of the sphere (M) and the distance from its center.
For a point inside a solid sphere (where r < R, R being the radius of the sphere), the gravitational field is given by:
Er=G⋅Mrr2
where Mr is the mass enclosed within radius r. According to Gauss's law for gravitation, the mass enclosed within a radius r is proportional to the volume of the sphere of radius r:
Mr=MR3⋅r3
Therefore, the gravitational field inside the sphere becomes:
Er=G⋅(MR3⋅r3)r2=G⋅MR3⋅r
This shows that the gravitational field inside the sphere increases linearly with r.
For a point outside the solid sphere (where r > R), the gravitational field is given by:
Er=G⋅Mr2
This indicates that the gravitational field outside the sphere decreases with the square of the distance from the center of the sphere.
- Inside the sphere, the gravitational field increases linearly with distance from the center.
- Outside the sphere, the gravitational field decreases with the square of the distance from the center.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.4
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
The density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
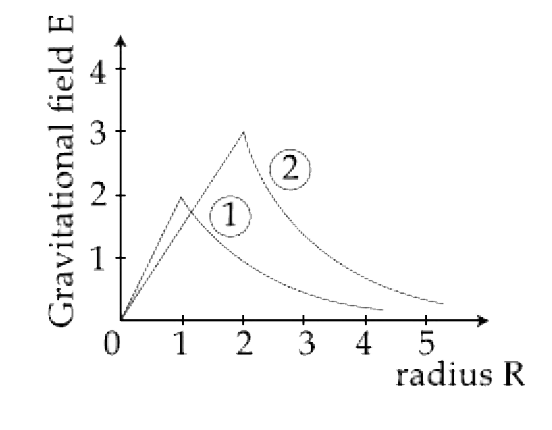
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
View SolutionThe gravitational field due to a mass distribution is E=Ax2 in x-direction. Here, A is a constant, Taking the gravitational potential to be zero at infinity, potential at x is
View SolutionCalcualte the intensily of gravitational field due to a body of mass 20kg at a distance of 50cm from the body ?
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe gravitational field due to a mass distribution is E=K/x3 in the x - direction. ( K is a constant). Taking the gravitational potential to be zero at infinity, its value at a distance x is
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionIntensity of gravitational field inside the hollow spherical shell is
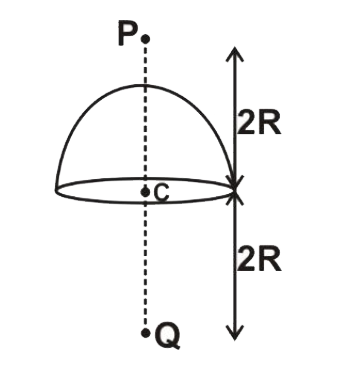
View SolutionIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
View Solution
