How will you connect three resistors of and respectively so as to obtain a resultant resistance of ? Draw the diagram to show the arrangement.
The correct Answer is:
To connect three resistors of 2Ω, 3Ω, and 5Ω to obtain a resultant resistance of 2.5Ω, we can follow these steps:
Step 1: Understanding Series and Parallel Connections
- In a series connection, the total resistance (R_total) is the sum of the individual resistances:
\(
R_{\text{total}} = R_1 + R_2 + R_3
\)
- In a parallel connection, the total resistance (R_total) can be calculated using the formula:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
Step 2: Connecting 2Ω and 3Ω in Series
- First, we connect the 2Ω and 3Ω resistors in series:
\(
R_{A} = 2Ω + 3Ω = 5Ω
\)
- The equivalent resistance of this series connection (R_A) is 5Ω.
Step 3: Connecting the Resultant Resistance in Parallel with 5Ω
- Now, we connect this resultant 5Ω resistance in parallel with the 5Ω resistor:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_A} + \frac{1}{5Ω}
\)
\(
\frac{1}{R_{\text{total}}} = \frac{1}{5Ω} + \frac{1}{5Ω}
\)
\(
\frac{1}{R_{\text{total}}} = \frac{2}{5Ω}
\)
\(
R_{\text{total}} = \frac{5Ω}{2} = 2.5Ω
\)
Step 4: Drawing the Circuit Diagram
- The circuit diagram will show the 2Ω and 3Ω resistors connected in series, and this combination connected in parallel with the 5Ω resistor.
Final Arrangement
- The final arrangement is:
- 2Ω and 3Ω in series (resulting in 5Ω)
- This 5Ω in parallel with the 5Ω resistor
Diagram
±−−(2Ω)−−−(3Ω)−−−+∣|∣|±−−−−−−−(5Ω)−−−−−+
Summary
- By connecting the 2Ω and 3Ω resistors in series to form a 5Ω resistance and then connecting this 5Ω resistance in parallel with the other 5Ω resistor, we achieve a resultant resistance of 2.5Ω.
- In a series connection, the total resistance (R_total) is the sum of the individual resistances:
\(
R_{\text{total}} = R_1 + R_2 + R_3
\)
- In a parallel connection, the total resistance (R_total) can be calculated using the formula:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
- First, we connect the 2Ω and 3Ω resistors in series:
\(
R_{A} = 2Ω + 3Ω = 5Ω
\)
- The equivalent resistance of this series connection (R_A) is 5Ω.
- Now, we connect this resultant 5Ω resistance in parallel with the 5Ω resistor:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_A} + \frac{1}{5Ω}
\)
\(
\frac{1}{R_{\text{total}}} = \frac{1}{5Ω} + \frac{1}{5Ω}
\)
\(
\frac{1}{R_{\text{total}}} = \frac{2}{5Ω}
\)
\(
R_{\text{total}} = \frac{5Ω}{2} = 2.5Ω
\)
- The circuit diagram will show the 2Ω and 3Ω resistors connected in series, and this combination connected in parallel with the 5Ω resistor.
- The final arrangement is:
- 2Ω and 3Ω in series (resulting in 5Ω)
- This 5Ω in parallel with the 5Ω resistor
±−−(2Ω)−−−(3Ω)−−−+∣|∣|±−−−−−−−(5Ω)−−−−−+
- By connecting the 2Ω and 3Ω resistors in series to form a 5Ω resistance and then connecting this 5Ω resistance in parallel with the other 5Ω resistor, we achieve a resultant resistance of 2.5Ω.
Topper's Solved these Questions
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Very Short Answer Type Questions
1 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Short Answer Type Questions
2 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Sample Problem
1 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - NCERT BOOK
2 Videos
Similar Questions
Knowledge Check
If you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
A B
B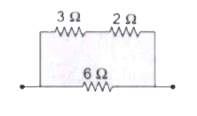 C
C Dnone of these
Dnone of theseIf you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
A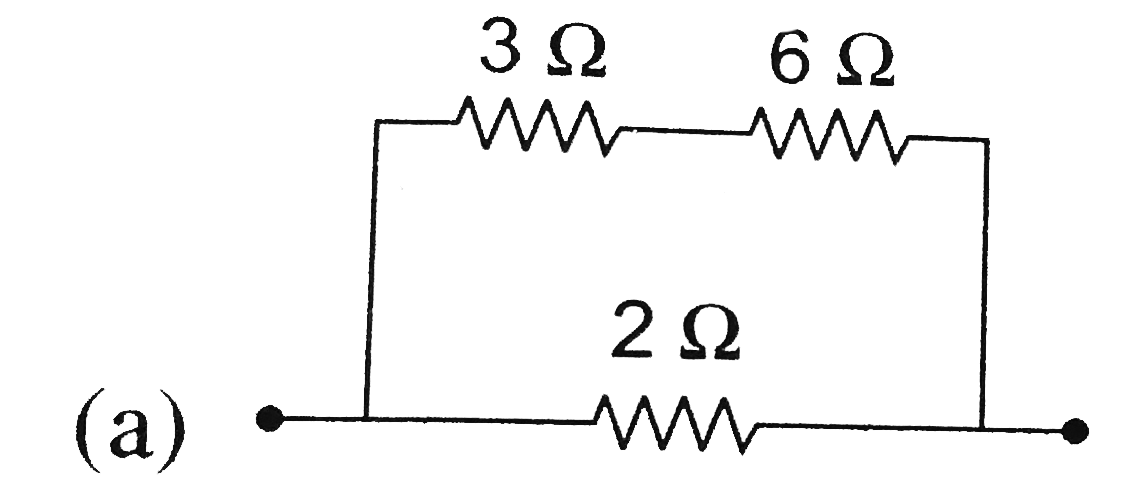 B
B C
C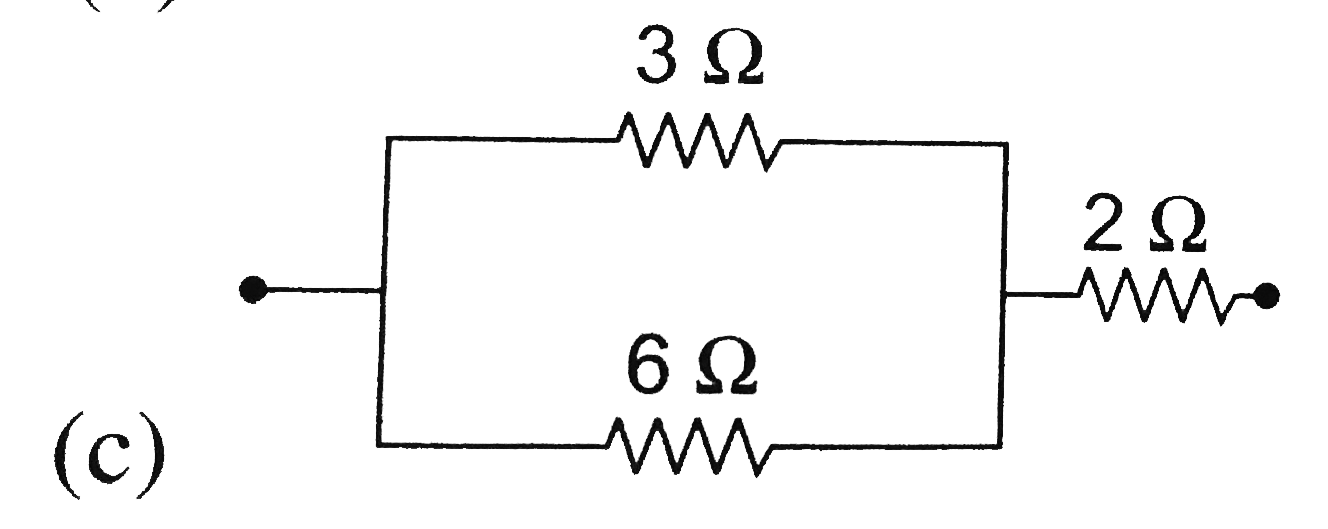 Dnone
Dnone
How will you join the resistors of resistances 3Ω,6Ω and 8Ω to get an equivalent resistance of 10Ω?
View SolutionHow can the resistances of 2Ω,3Ω and 6Ω be connected to give an effective resistance of 4Ω ?
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionHow can three resistors of resistance 2Ω,3Ω and 6Ω be connected to give a total resistance of (i) 4Ω, (ii) 1Ω?
View SolutionThree resistors, each of 2Ω, are connected together so that their total resistance is 3Ω. Draw a diagram to show this arrangement and check it by calculation.
View Solution
