(i) One end of a uniform glass capillary tube of radius r=0.025 cm is immersed vertically in water to a depth h=1cm. Contact angle is 0∘, surface tension of water is 7.5×10–2N/m, density of water is ρ=103kg/m3 and atmospheric pressure is Po=105N/m2
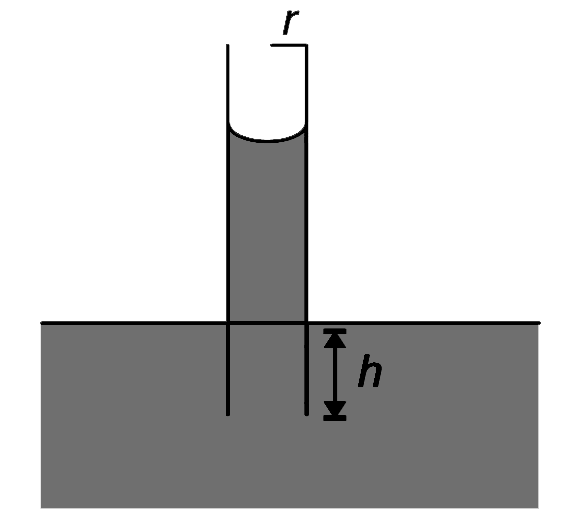
Find the excess pressure to be applied on the water in the capillary tube so that -
(a) The water level in the tube becomes same as that in the vessel.
(b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density ρ1 and ρ2(ρ2>ρ1). A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid.
The correct Answer is:(1) (a) 600Pa (b) Yes (3) T=r2(ρ2−ρ1)gh
Step by step video, text & image solution for (i) One end of a uniform glass capillary tube of radius r = 0.025 cm is immersed vertically in water to a depth h = 1cm. Contact angle is 0^(@), surface tension of water is 7.5 × 10–2 N//m, density of water is rho = 10^(3) kg//m^(3) and atmospheric pressure is P_(o) = 10^(5) N // m^(2) Find the excess pressure to be applied on the water in the capillary tube so that - (a) The water level in the tube becomes same as that in the vessel. (b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density rho_(1) and rho_(2) (rho_(2) gt rho_(1)). A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A small hollow sphere which has a small hole in it is immersed in water to a depth of 40 cm, before any water is penetrated into it. If the surface tensionof water si 0.073Nm−1, find the radius of the hole.
View SolutionWhen a glass capillary tube of radius 0.015 cm is dipped in water, the water rises to a height of 15 cm within it. Assuming contact angle between water and glass to be 0°, the surface tension of water.is [pwaler = 1000 kg m−3 , g = 9.81 ms∧(−2) ]
View Solution
Knowledge Check
One end of a uniform glass capillary tube of radius r = 0.025 cm is immersed vertically in water to a depth h = 1cm. The excess pressure (in Nm−2) required to blow an air bubble out of the tube (Given , surface tension of water =7×10−2Nm−1, density of water =10−3kgm−3 and acceleration due to gravity =10ms−2)
A0.0048×105B0.0066×105C1.0048×105D1.0066×105A capillary tube of radius 0.25 mm is submerged vertically in water so that 25 mm of its length is outside water. The radius of curvature of the meniscus will be
(surface tension of water =75×10−3 N/m)A0.2 mmB0.4 mmC0.6 mmD0.8 mmA glass capillary of radius 0.4 mm is inclined at 60∘ with the vertical in water. Find the length of water in the capillary tube.
(Given, surface tension of water =7×10−2N−1).A7.1 cmB3.6 cmC1.8 cmD0.9 cm
A glass capillary tube of inner diameter 0.28 mm is lowered vertically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as the vessel in Nm2 is (surface tension of water =0.07Nm atmospheric pressure =105Nm2
View SolutionOne end of a glass capillary tube with a radius r=0.05cm is immersed into water to a depth of h=2cm.Excess pressure required to blow an air bubble out of the lower end of the tube will be (S.T of water =70dyne/cm).Take g=980cm/s2.
View SolutionIf a capillary tube of radius 2×10−4 m is is dipped vertically in a water of surface tension 7×10−2 N/m and density 103kg/m3 then the height to which water rises will be
View SolutionWhen a glass capilary tube of the radius 0.015 cm is dipped in water, the water rises to a heigth of 15 cm within it. Assuming the contact angle between water and glass to be 0∘, the surface tension of water is
[ρwater=1000kgm−3,g=9.81ms−2]
View Solutionf the surface tension of water is 7×10−2 N/m then the rise of water is 7×10−2 N/m then the rise of water in a capillary tube of diameter 0.35 mm will be
View Solution
