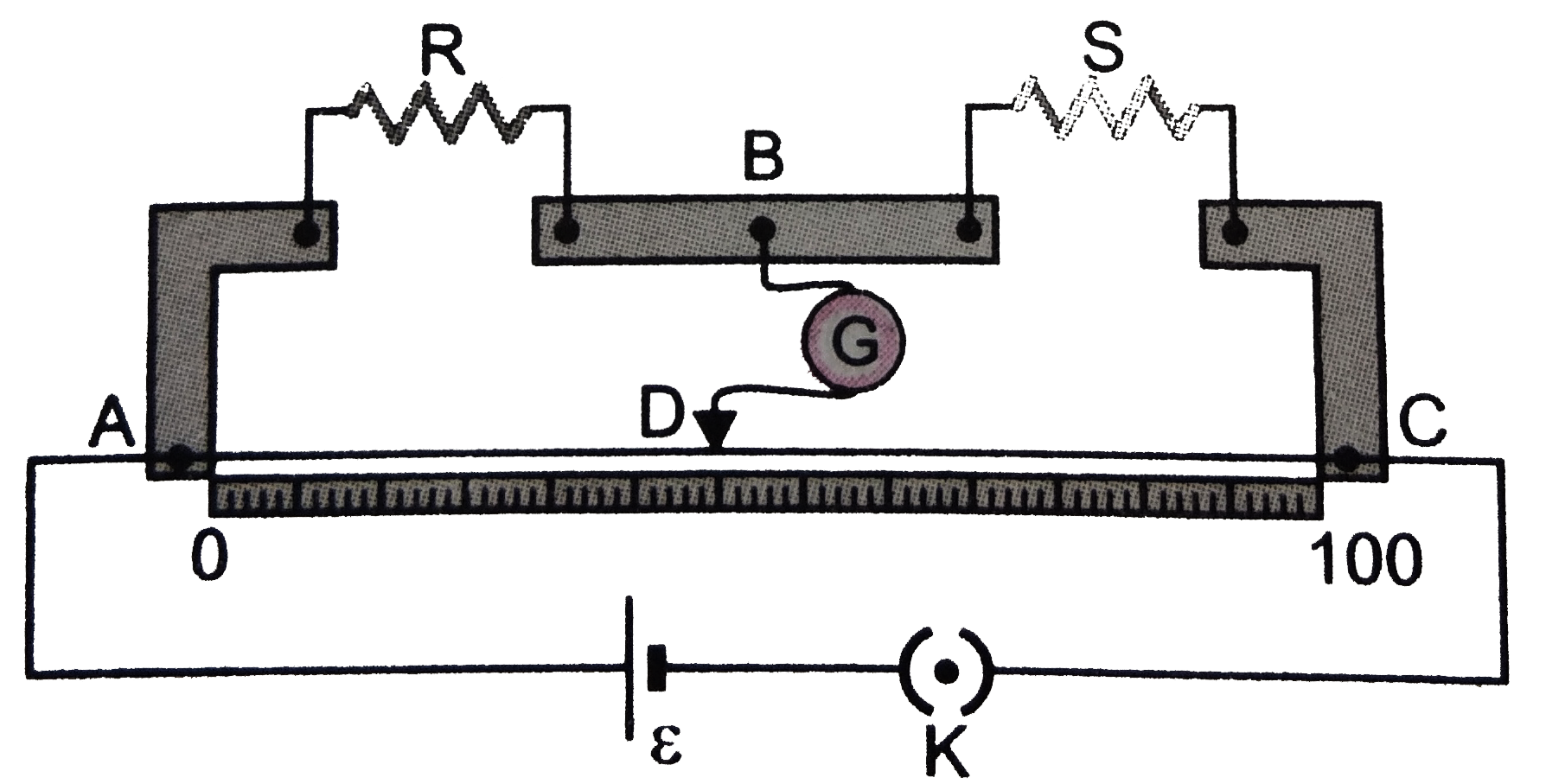
(i) State the principle of working of a meter bridge.
(ii) In a meter bridge balance point is found at a distance with resistances R and S as shown in the figure. When an unknown resistance X is connected in parallel with the resistance S, the balance point shifts to a distance . Find the expression for X in terms of and S.
Solution:
(i) Principle of Working of a Meter Bridge:
The meter bridge operates on the principle of the Wheatstone bridge. It consists of a one-meter-long uniform wire that is used to compare two resistances. When a current passes through the wire, a jockey is used to find a point along the wire where the galvanometer shows no deflection (null point). At this point, the ratio of the resistances on either side of the bridge is equal to the ratio of the lengths of the wire on either side of the jockey.
Mathematically, if R is the known resistance and S is the unknown resistance, and L1 is the length of the wire on the side of R and (100 - L1) is the length on the side of S, then:
RS=L1100−L1
(ii) Finding the Expression for X:
1. Initial Setup:
- Initially, the balance point is at distance L1 with resistances R and S.
- When an unknown resistance X is connected in parallel with S, the new balance point shifts to L2.
2. Using the Balance Condition:
- For the new setup with X in parallel with S, the equivalent resistance Rp can be expressed as:
1Rp=1X+1S⟹Rp=S⋅XS+X
3. Setting Up the New Balance Equation:
- At the new balance point, we have:
RRp=L2100−L2
- Substituting Rp into the equation:
RS⋅XS+X=L2100−L2
4. Cross-Multiplying:
R⋅(S+X)=S⋅X⋅L2100−L2
5. Rearranging the Equation:
- Rearranging gives:
R⋅S+R⋅X=S⋅X⋅L2100−L2
6. Dividing by the First Equation:
- From the first balance condition:
RS=L1100−L1
- Rearranging gives:
R=S⋅L1100−L1
7. Substituting R in the New Equation:
- Substitute R into the rearranged equation:
S⋅L1100−L1⋅S+S⋅L1100−L1⋅X=S⋅X⋅L2100−L2
8. Simplifying:
- Cancel S from both sides (assuming S≠0):
L1100−L1+L1100−L1⋅XS=X⋅L2S⋅(100−L2)
9. Final Expression for X:
- After simplification, we find:
X=L1⋅(100−L2)L2−L1⋅S
- Initially, the balance point is at distance L1 with resistances R and S.
- When an unknown resistance X is connected in parallel with S, the new balance point shifts to L2.
- For the new setup with X in parallel with S, the equivalent resistance Rp can be expressed as:
1Rp=1X+1S⟹Rp=S⋅XS+X
- At the new balance point, we have:
RRp=L2100−L2
- Substituting Rp into the equation:
RS⋅XS+X=L2100−L2
R⋅(S+X)=S⋅X⋅L2100−L2
- Rearranging gives:
R⋅S+R⋅X=S⋅X⋅L2100−L2
- From the first balance condition:
RS=L1100−L1
- Rearranging gives:
R=S⋅L1100−L1
- Substitute R into the rearranged equation:
S⋅L1100−L1⋅S+S⋅L1100−L1⋅X=S⋅X⋅L2100−L2
- Cancel S from both sides (assuming S≠0):
L1100−L1+L1100−L1⋅XS=X⋅L2S⋅(100−L2)
- After simplification, we find:
X=L1⋅(100−L2)L2−L1⋅S
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Answer the following:
(a) Write the principle of working of a metre bridge.
(b) In a metre bridge, the balance point is found at a distance I1 with resistances R and S as shown in the figure.

An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance I2 , Obtain a formula for X in terms of I1,I2 and S .
View SolutionIn a meter bridge,
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
View SolutionIn a meter bridge, the null point is found at a distance of l1cm from A. if now a resistance of X is connected in parallel with S, the null point occurs at l2cm. Obtain a formula for X is terms of l1,l2andS.
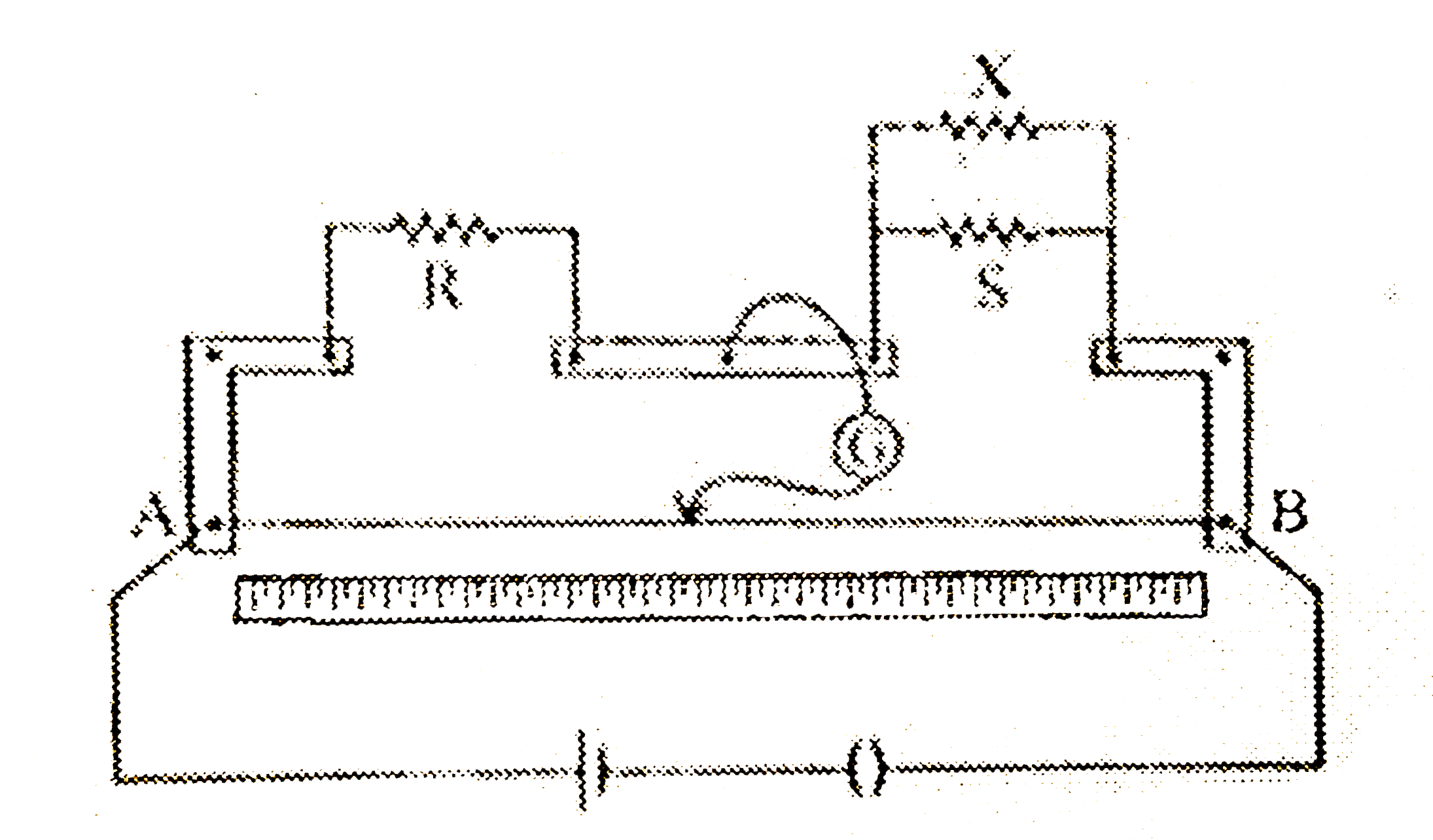
View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
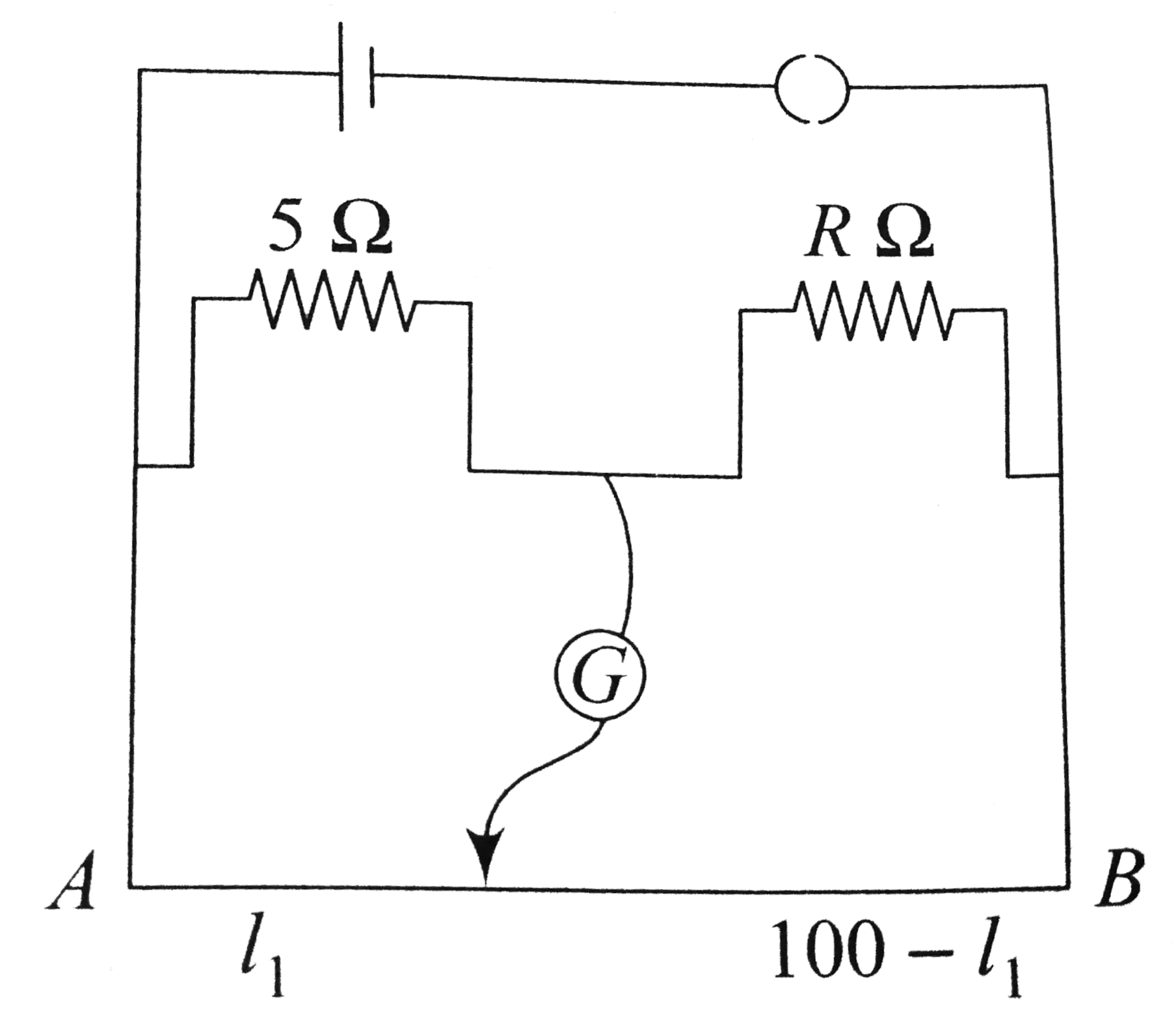
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
View Solution
