In meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
0.25Ω
0.4Ω
0.5Ω
4Ω
The correct Answer is:A
To find the unknown resistance using the meter bridge method, we can follow these steps:
Step 1: Understand the Meter Bridge Principle
The meter bridge is based on the principle of Wheatstone bridge. When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths on the bridge wire.
Step 2: Write the Formula
The formula for the meter bridge is given by:
SR=L100−L
where:
- S = unknown resistance
- R = known resistance (1 ohm in this case)
- L = balancing length from the left (20 cm in this case)
Step 3: Substitute the Known Values
We know:
- R=1Ω
- L=20cm
Substituting these values into the formula gives:
S1=20100−20
Step 4: Simplify the Equation
Now simplify the right side:
S1=2080
Step 5: Calculate the Unknown Resistance
Now calculate S:
S=2080=14=0.25Ω
Final Answer
The value of the unknown resistance S is 0.25Ω.
---
The meter bridge is based on the principle of Wheatstone bridge. When the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths on the bridge wire.
The formula for the meter bridge is given by:
SR=L100−L
where:
- S = unknown resistance
- R = known resistance (1 ohm in this case)
- L = balancing length from the left (20 cm in this case)
We know:
- R=1Ω
- L=20cm
S1=20100−20
Now simplify the right side:
S1=2080
Now calculate S:
S=2080=14=0.25Ω
The value of the unknown resistance S is 0.25Ω.
Similar Questions
In a metere bridge, the balance length from left end (standard resistance of 1Ω is in theright gap) is found to be 20cm the length of Resistance in left gap is 12m and radiusis 2mm its specific resistance is
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
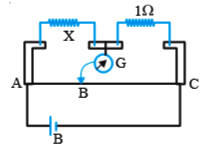
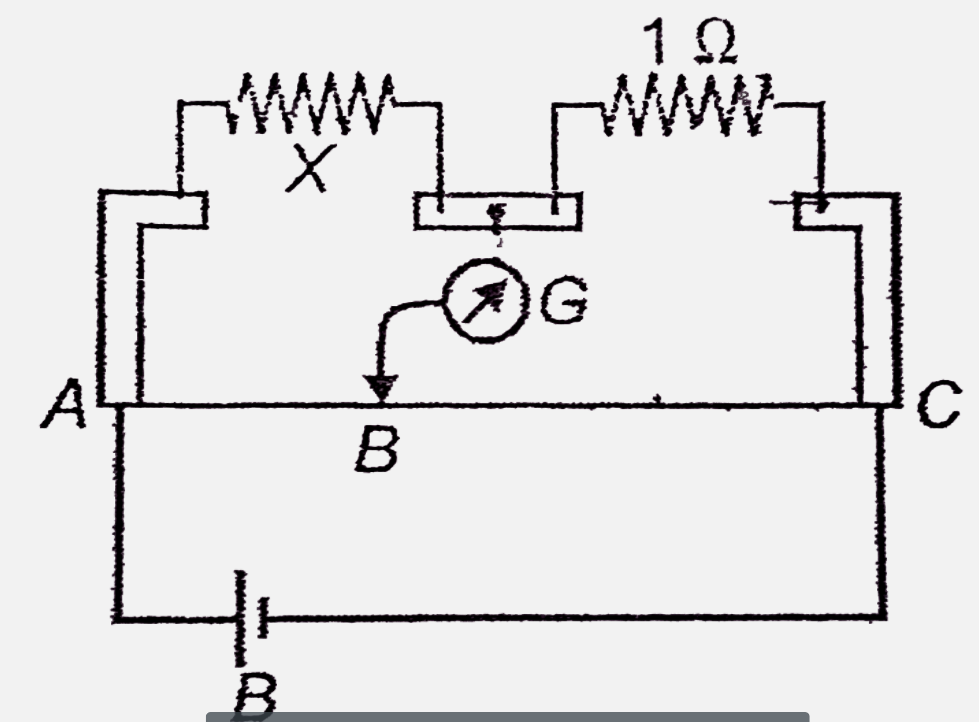
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
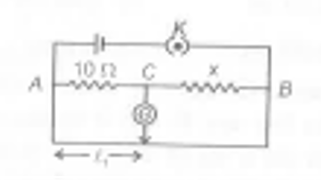
View SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be
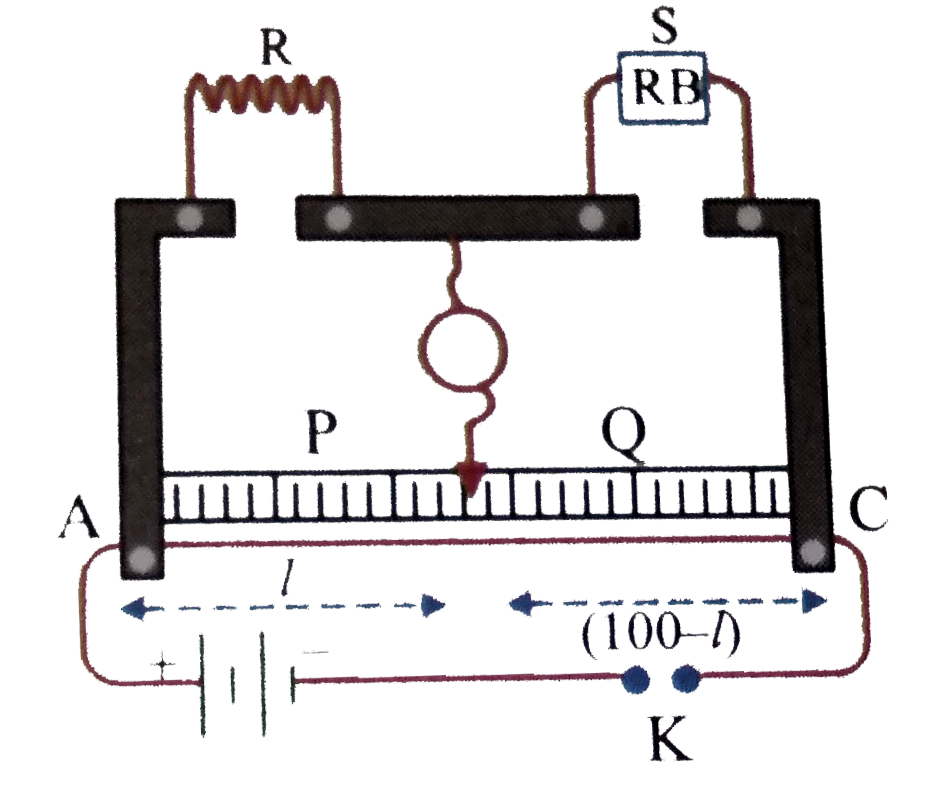
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
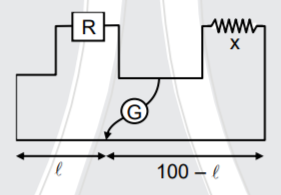
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is

View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View Solution
