Identify the correct order in which the value of normal reaction increases, (object is placed on rough horizontal surface)
i) The object is pushed with the force F at an angle 'q' with horizontal
ii) The object is pulled with the force F at an angle 'q' with horizontal
iii) The object is pushed down with the force F normally
iv) The object pulled up with the force F normally
i, ii, iii, iv
iv, ii, i, iii
i, iii, ii, iv
ii, iv, iii, i
The correct Answer is:B
To solve the problem of determining the correct order in which the value of normal reaction increases when an object is placed on a rough horizontal surface and subjected to different forces, we will analyze each case step by step.
Step 1: Understand the Forces Acting on the Object
For an object of mass M placed on a horizontal surface, the forces acting on it include:
- The weight of the object, Mg, acting downwards.
- The normal reaction force, N, acting upwards.
- Any applied force F at an angle θ with respect to the horizontal.
Step 2: Analyze Each Case
Case i: Object is Pushed with Force F at Angle θ
- The vertical component of the force F is Fsinθ acting downwards.
- The normal reaction N1 can be expressed as:
N1=Mg+Fsinθ
Case ii: Object is Pulled with Force F at Angle θ
- The vertical component of the force F is Fsinθ acting upwards.
- The normal reaction N2 can be expressed as:
N2=Mg−Fsinθ
Case iii: Object is Pushed Down with Force F Normally
- Both the weight Mg and the force F act downwards.
- The normal reaction N3 can be expressed as:
N3=Mg+F
Case iv: Object is Pulled Up with Force F Normally
- The weight Mg acts downwards while the force F acts upwards.
- The normal reaction N4 can be expressed as:
N4=Mg−F
Step 3: Compare the Normal Reactions
Now we have the expressions for the normal reactions:
1. N1=Mg+Fsinθ
2. N2=Mg−Fsinθ
3. N3=Mg+F
4. N4=Mg−F
To determine the order of these normal reactions, we need to consider the effects of F and sinθ:
- Since sinθ ranges from 0 to 1, N2 (which decreases with Fsinθ) will be the smallest when Fsinθ is maximized.
- N4 is also reduced by F, but it is less than N3 and N1 since both of these add to the weight.
Step 4: Arrange in Increasing Order
1. Smallest: N4=Mg−F (pulled up normally)
2. Next: N2=Mg−Fsinθ (pulled with force at angle)
3. Next: N1=Mg+Fsinθ (pushed with force at angle)
4. Largest: N3=Mg+F (pushed down normally)
Final Order
Thus, the correct order in which the value of normal reaction increases is:
N4<N2<N1<N3
For an object of mass M placed on a horizontal surface, the forces acting on it include:
- The weight of the object, Mg, acting downwards.
- The normal reaction force, N, acting upwards.
- Any applied force F at an angle θ with respect to the horizontal.
- The vertical component of the force F is Fsinθ acting downwards.
- The normal reaction N1 can be expressed as:
N1=Mg+Fsinθ
- The vertical component of the force F is Fsinθ acting upwards.
- The normal reaction N2 can be expressed as:
N2=Mg−Fsinθ
- Both the weight Mg and the force F act downwards.
- The normal reaction N3 can be expressed as:
N3=Mg+F
- The weight Mg acts downwards while the force F acts upwards.
- The normal reaction N4 can be expressed as:
N4=Mg−F
Now we have the expressions for the normal reactions:
1. N1=Mg+Fsinθ
2. N2=Mg−Fsinθ
3. N3=Mg+F
4. N4=Mg−F
- Since sinθ ranges from 0 to 1, N2 (which decreases with Fsinθ) will be the smallest when Fsinθ is maximized.
- N4 is also reduced by F, but it is less than N3 and N1 since both of these add to the weight.
1. Smallest: N4=Mg−F (pulled up normally)
2. Next: N2=Mg−Fsinθ (pulled with force at angle)
3. Next: N1=Mg+Fsinθ (pushed with force at angle)
4. Largest: N3=Mg+F (pushed down normally)
Thus, the correct order in which the value of normal reaction increases is:
N4<N2<N1<N3
Similar Questions
A block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
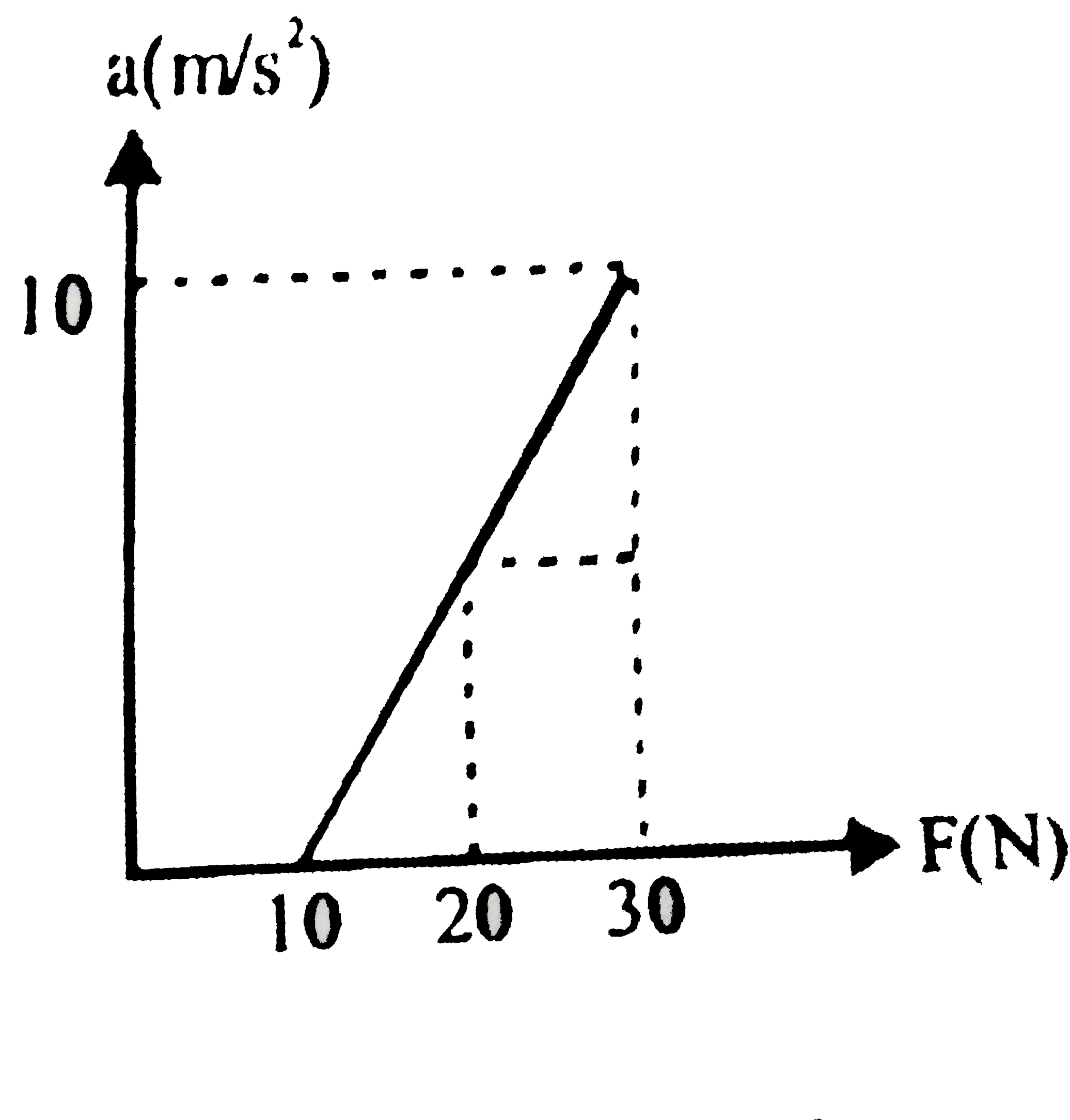
View SolutionA block placed on a rough horizontal surface is pushed with a force F acting horizontally on the block. The magnitude of F is increased and acceleration produced is plotted in the graph shown.
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionFor an object projected from ground with speed u horizontal range is two times the maximum height attained by it. The horizontal range of object is
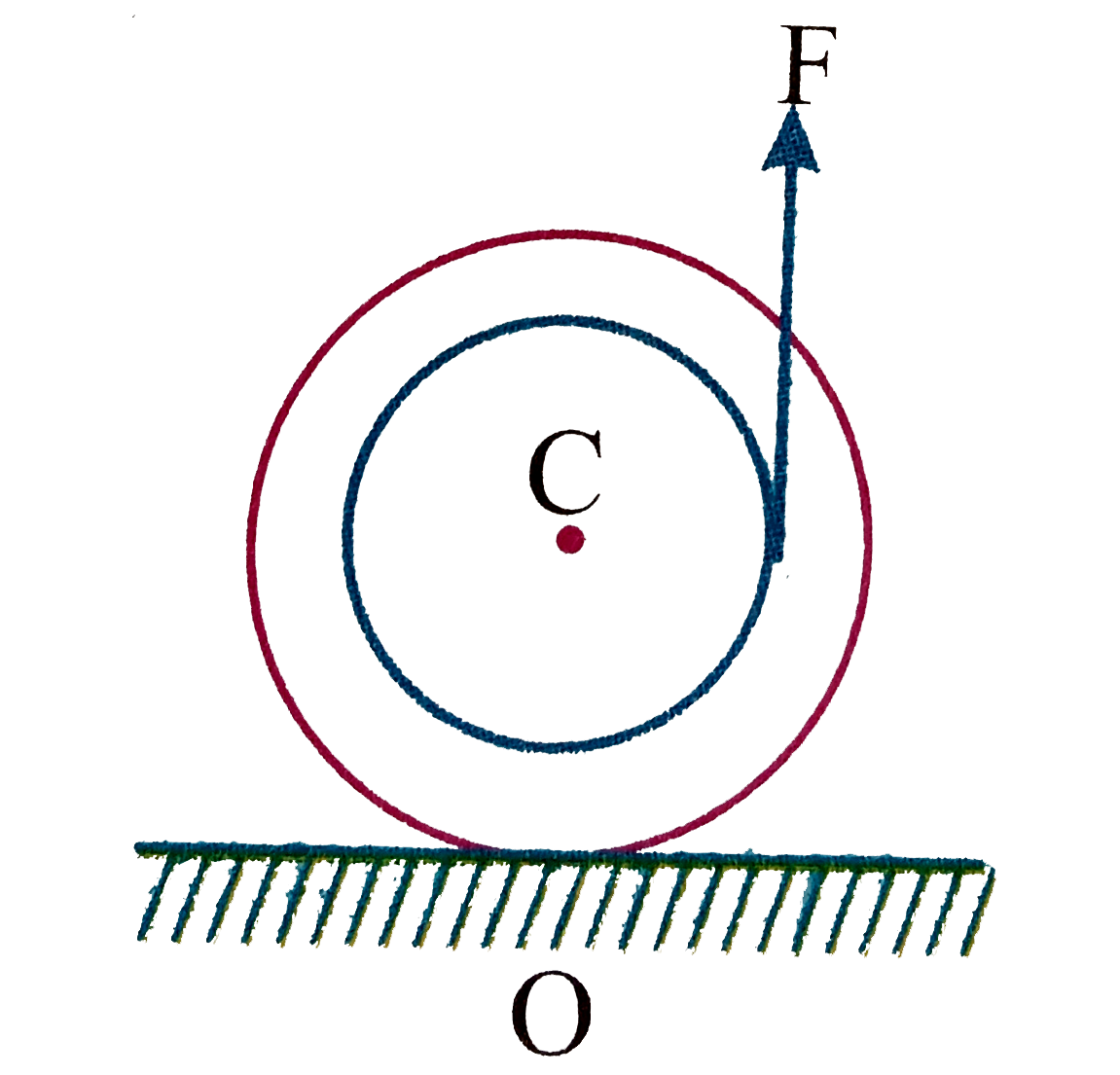
View SolutionA yo-yo is placed on a rough horizontal surface and a constant force F, which is less than its weight, pulls it vertically. Due to this
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View SolutionA block placed on a rough horizontal surface is pulled by a horizontal force F Let f be the force applied by the rough surface on the block . Plot a graph of f versus F .
View SolutionAn object is projected with a velocity of 30ms−1 at an angle of 60∘ with the horizontal. Determine the horizontal range covered by the object.
View SolutionA body of weight 20N is on a horizontal surface, minimum force applied to pull it when applied force makes an angle 60° with horizontal (angle of friction a = 30°) is
View Solution
