A body of weight 20N is on a horizontal surface, minimum force applied to pull it when applied force makes an angle 60° with horizontal (angle of friction a = 30°) is
20 N
20√3N
20√3N
20 N
The correct Answer is:C
To solve the problem, we need to determine the minimum force required to pull a body of weight 20 N when the applied force makes an angle of 60° with the horizontal, given that the angle of friction (α) is 30°.
1. Identify Given Values:
- Weight of the body (W) = 20 N
- Angle of applied force (θ) = 60°
- Angle of friction (α) = 30°
2. Calculate the Coefficient of Static Friction (μ):
- The coefficient of static friction can be calculated using the angle of friction:
μ=tan(α)=tan(30°)=1√3
3. Resolve the Applied Force (F):
- Let the applied force be F.
- The horizontal component of the applied force is:
Fhorizontal=Fcos(60°)=F2
- The vertical component of the applied force is:
Fvertical=Fsin(60°)=F√32
4. Calculate the Normal Force (N):
- The normal force can be calculated as:
N=W−Fvertical=20N−F√32
5. Use the Condition for Motion:
- For the body to just start moving, the horizontal component of the applied force must equal the maximum static friction:
Fhorizontal=μN
- Substituting the values we have:
F2=μ(20N−F√32)
- Substitute μ=1√3:
F2=1√3(20N−F√32)
6. Solve for F:
- Multiply both sides by √3:
F√32=20N−F√32
- Rearranging gives:
F√32+F√32=20N
F√3=20N
F=20N√3≈11.55N
Final Answer:
The minimum force required to pull the body is:
F=20√3 N
- Weight of the body (W) = 20 N
- Angle of applied force (θ) = 60°
- Angle of friction (α) = 30°
- The coefficient of static friction can be calculated using the angle of friction:
μ=tan(α)=tan(30°)=1√3
- Let the applied force be F.
- The horizontal component of the applied force is:
Fhorizontal=Fcos(60°)=F2
- The vertical component of the applied force is:
Fvertical=Fsin(60°)=F√32
- The normal force can be calculated as:
N=W−Fvertical=20N−F√32
- For the body to just start moving, the horizontal component of the applied force must equal the maximum static friction:
Fhorizontal=μN
- Substituting the values we have:
F2=μ(20N−F√32)
- Substitute μ=1√3:
F2=1√3(20N−F√32)
- Multiply both sides by √3:
F√32=20N−F√32
- Rearranging gives:
F√32+F√32=20N
F√3=20N
F=20N√3≈11.55N
The minimum force required to pull the body is:
F=20√3 N
Similar Questions
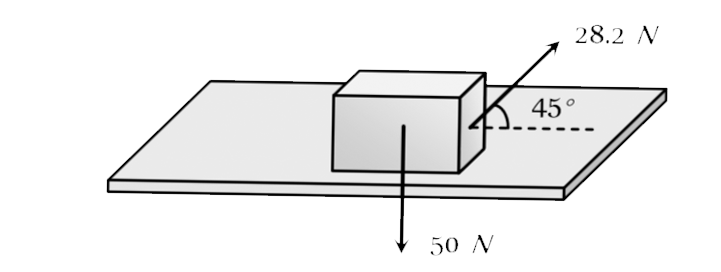
A body of weight 50 N placed on a horizontal surface is just moved by a force of 28.2 N. the frictional force and the narmal reaction are
View SolutionA block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View SolutionA body of mass 10 kg is placed on rough surface, pulled by force F making an angle of 30∘ above the horizontal. If the angle of friction is also 30∘, then the minimum magnitude of force F required to move the body is equal to ( take, g=10ms−2)
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionAssertion: A body of weight 10N (W) is at rest on an inclined plane (μ=√32) making an angle of 30∘ with the horizontal. The force of friction acting on it is 5N
Reason: In above situation, the limiting force of friction is given by flimitting=μWcosθ=7.5N.
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.

View Solution
