If a partical moves in a potential energy held U=U0−ax+bx2, where are a and b partical constents obtian an expression for the force acting on if as a function of position. At what point does the force vanish? Is this a point of stable equilibriun ?
Calculate the force constant and friquency of the partical.
To solve the problem step by step, we will follow the instructions given in the question.
Step 1: Obtain an expression for the force acting on the particle as a function of position.
The potential energy U is given by:
U=U0−ax+bx2
To find the force F acting on the particle, we use the relation:
F=−dUdx
Now, we differentiate U with respect to x:
dUdx=ddx(U0−ax+bx2)=0−a+2bx=−a+2bx
Thus, the force F is:
F=−(−a+2bx)=a−2bx
Step 2: Determine the point where the force vanishes.
To find the point where the force vanishes, we set F=0:
a−2bx=0
Solving for x:
2bx=a⟹x=a2b
Step 3: Check if this point is a point of stable equilibrium.
To determine if this point is a stable equilibrium, we need to check the second derivative of the potential energy U:
d2Udx2=ddx(−a+2bx)=2b
Since b is a positive constant, 2b>0. This indicates that the potential energy has a minimum at this point, confirming that it is a point of stable equilibrium.
Step 4: Calculate the force constant and frequency of the particle.
The force constant k is given by:
k=2b
The frequency f of the particle can be calculated using the formula:
f=12π√km=12π√2bm
Summary of Results:
1. Expression for force: F=a−2bx
2. Point where force vanishes: x=a2b
3. Stability: This point is a point of stable equilibrium.
4. Force constant: k=2b
5. Frequency: f=12π√2bm
1. Expression for force: F=a−2bx
2. Point where force vanishes: x=a2b
3. Stability: This point is a point of stable equilibrium.
4. Force constant: k=2b
5. Frequency: f=12π√2bm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example15videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionA particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionThe potential energy for a conservative force system is given by U=ax2−bx. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionThe potential energy for a conservative force system is given by U=ax2−bx. Where a and b are constants find out (a) The expression of force (b) Potential energy at equilibrium.
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionFigure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
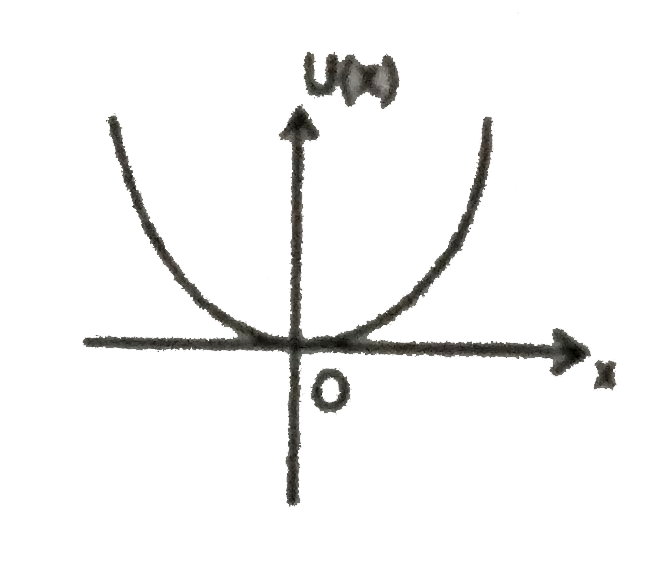 View Solution
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle isView Solution

