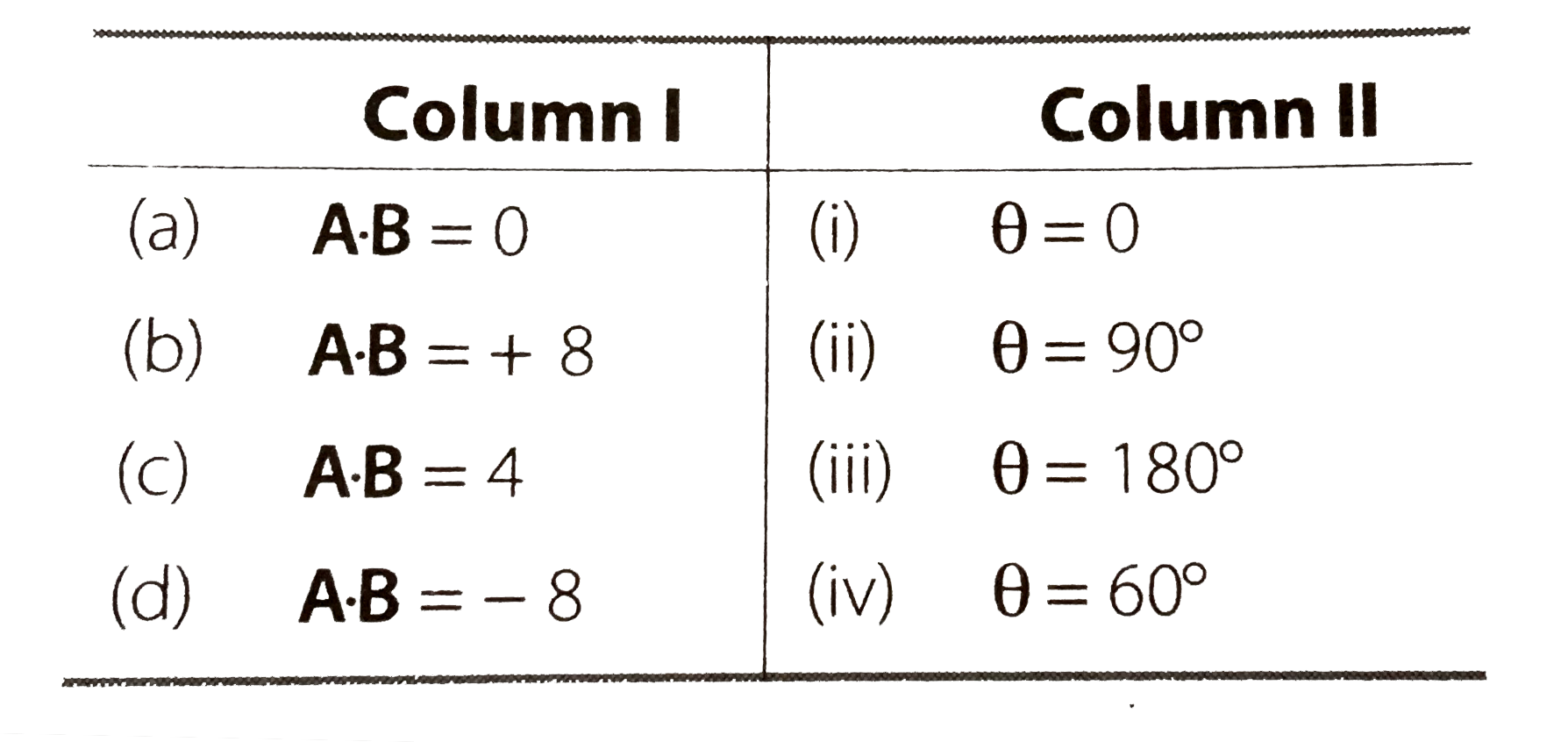
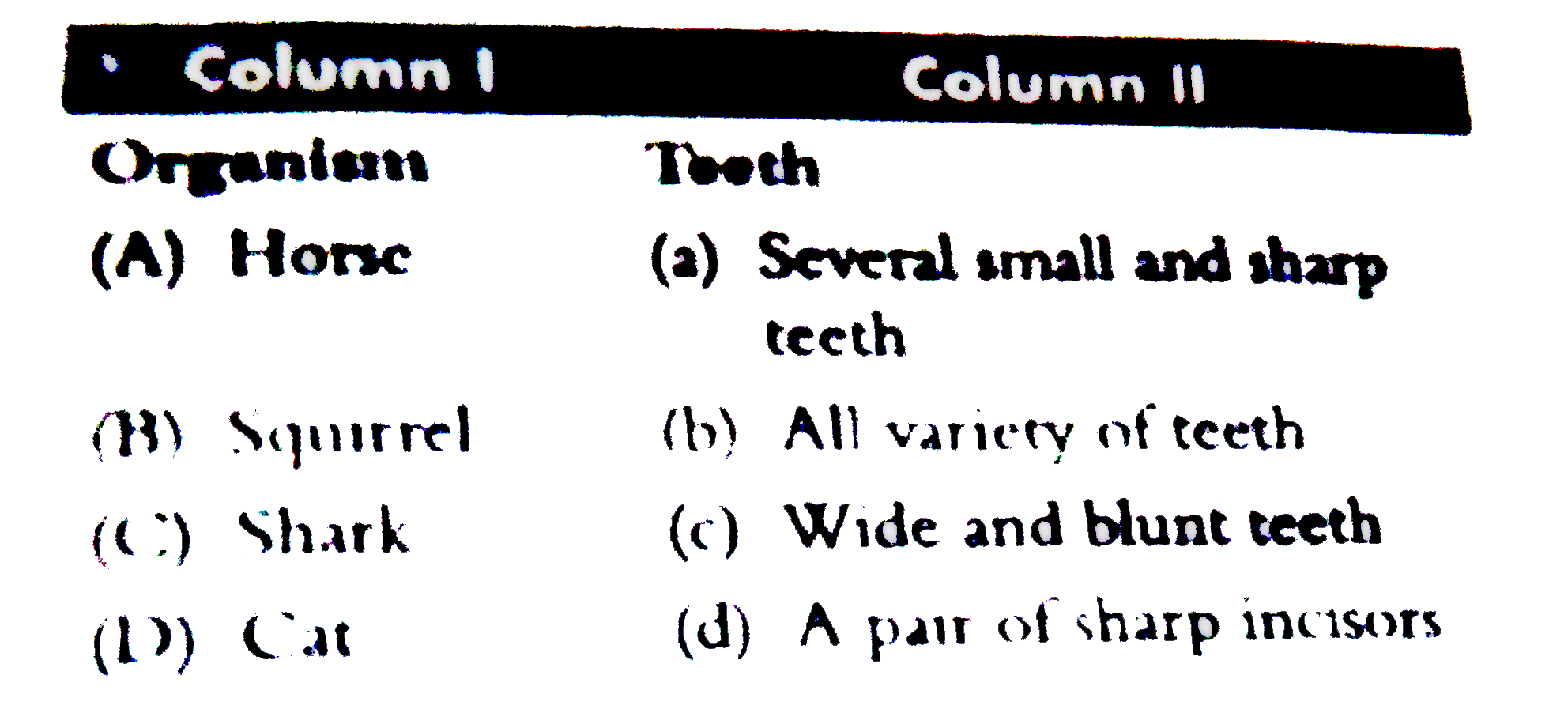If |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
Video Solution
Text Solution
Given |A| = and |B| =4
(a) A.B=ABcosθ=0 ⇒ 2×4cosθ=0
⇒ cosθ=0=cos90∘ ⇒ θ=90∘
∴ Option (a) matches with option (ii).
(b) A.B=ABcosθ=8 ⇒ 2×4cosθ=8
⇒ cosθ=1=cos0∘⇒ θ=0∘
∴Option (b) matches with option (i).
(c)A.B=ABcosθ=4 ⇒ 2×4cosθ=4
⇒cosθ=12=cos60∘ ⇒ θ=60∘
∴ Option (c) matches with option (iv).(d) A.B=ABcosθ=−8 ⇒ 2×4cosθ=−8
⇒ cosθ=−1=cos=−1=cos180∘⇒ θ=180∘
∴ Option (d) matches with option (iii)
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
If ∣∣→A∣∣=2and∣∣→B∣∣=4, then match the relations in column I with the ange θ between →Aand→B in column II.
Column I, Column II
(a) ∣∣→A×→B∣∣=0 , (i) θ=30∘
(b) ∣∣→A×→B∣∣=0 , (ii) θ=45∘
(c ) →A×→B∣=4 , (iii) θ=90∘
(d) ∣∣→A×x→B∣∣=4√2 , (iv) θ=0∘.View SolutionIf ∣∣→A∣∣=2and∣∣→B∣∣=4 , then match the relations in colum I with theange θ between →Aand→B in column II.
Column I , Column II
(a) →A.→B=0 , (i) θ =0<br>(b) vec A . Vec B= + 8,(ii) theta =90^@<br>(c) vec A .vec B =4,(iii) theta =180^@<br>(d) vec A .vec B =- 8,(iv) theta =60^@.View Solution
Knowledge Check
- Question 1 - Select One
IF ∣∣→A∣∣=2 and ∣∣→B∣∣=4, then match the relation in Column I with the angle θ between A and B in Column II.
Now, mark the correct above choice from the given codes :Ap-ii, q-i, r-iv,s-iiiBp-iv, q-iii,r-i,s-iiCp-I,q-iii,e-iv,s-iiDp-iii, q-iv, r-i ,s-ii - Question 2 - Select One
Match the column I with Column II
Aa-(iii), b-(iv), c-(i), d-(ii)Ba-(iii), b-(ii), c-(i), d-(iv)Ca-(i), b-(ii), c-(iv), d-(iii)Da-(ii), b-(i), c-(iii), d-(iv)
