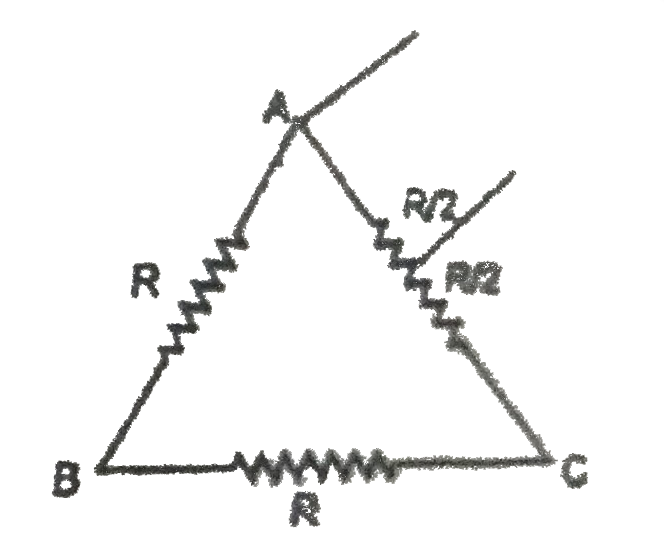
If an equilateral triangle is made of a uniform wire is resistance R, the equivalent resistance between the ends of sides is
The correct Answer is:C
To find the equivalent resistance between the ends of the sides of an equilateral triangle made of a uniform wire with total resistance R, we can follow these steps:
1. Understand the Structure:
- An equilateral triangle consists of three equal sides. When a uniform wire of resistance R is shaped into an equilateral triangle, the total resistance R is distributed equally among the three sides.
2. Calculate Resistance of Each Side:
- Since the total resistance R is divided equally among the three sides, the resistance of each side (let's call it Rs) is:
Rs=R3
3. Identify the Points of Interest:
- Let’s denote the vertices of the triangle as points P, Q, and R. We want to find the equivalent resistance between points P and Q.
4. Analyze the Current Flow:
- When a current enters at point P, it can either flow directly to point Q through one side or split and flow through the other two sides before reaching point Q.
5. Determine the Configuration:
- The two sides PR and QR are in parallel when considering the current flowing from P to Q. The resistance of side PR is Rs and the resistance of side QR is also Rs.
6. Calculate the Equivalent Resistance of the Parallel Combination:
- The equivalent resistance RPQ for two resistances Rs in parallel is given by:
1RPQ=1Rs+1Rs=2Rs
- Substituting Rs=R3:
1RPQ=2R3=6R
- Therefore, the equivalent resistance RPQ is:
RPQ=R6
7. Add the Resistance of the Direct Path:
- The direct path from P to Q through one side of the triangle also has resistance Rs which is R3.
8. Combine the Resistances:
- The equivalent resistance Req between points P and Q is the sum of the equivalent resistance of the parallel combination and the resistance of the direct path:
Req=RPQ+Rs=R6+R3
- Converting R3 to sixths:
Req=R6+2R6=3R6=R2
Final Answer:
The equivalent resistance between the ends of the sides of the equilateral triangle is:
Req=R2
- An equilateral triangle consists of three equal sides. When a uniform wire of resistance R is shaped into an equilateral triangle, the total resistance R is distributed equally among the three sides.
2. Calculate Resistance of Each Side:
- Since the total resistance R is divided equally among the three sides, the resistance of each side (let's call it Rs) is:
Rs=R3
- Let’s denote the vertices of the triangle as points P, Q, and R. We want to find the equivalent resistance between points P and Q.
- When a current enters at point P, it can either flow directly to point Q through one side or split and flow through the other two sides before reaching point Q.
- The two sides PR and QR are in parallel when considering the current flowing from P to Q. The resistance of side PR is Rs and the resistance of side QR is also Rs.
- The equivalent resistance RPQ for two resistances Rs in parallel is given by:
1RPQ=1Rs+1Rs=2Rs
- Substituting Rs=R3:
1RPQ=2R3=6R
- Therefore, the equivalent resistance RPQ is:
RPQ=R6
- The direct path from P to Q through one side of the triangle also has resistance Rs which is R3.
- The equivalent resistance Req between points P and Q is the sum of the equivalent resistance of the parallel combination and the resistance of the direct path:
Req=RPQ+Rs=R6+R3
- Converting R3 to sixths:
Req=R6+2R6=3R6=R2
The equivalent resistance between the ends of the sides of the equilateral triangle is:
Req=R2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B isA3R4B5R6C7R12D4R3In the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and C isA3R4B5R6C7R12D4R3In the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and G isA3R4B5R6C7R12D4R3
Find the equivalent resistance between A & B if all resistance are 'R' ?

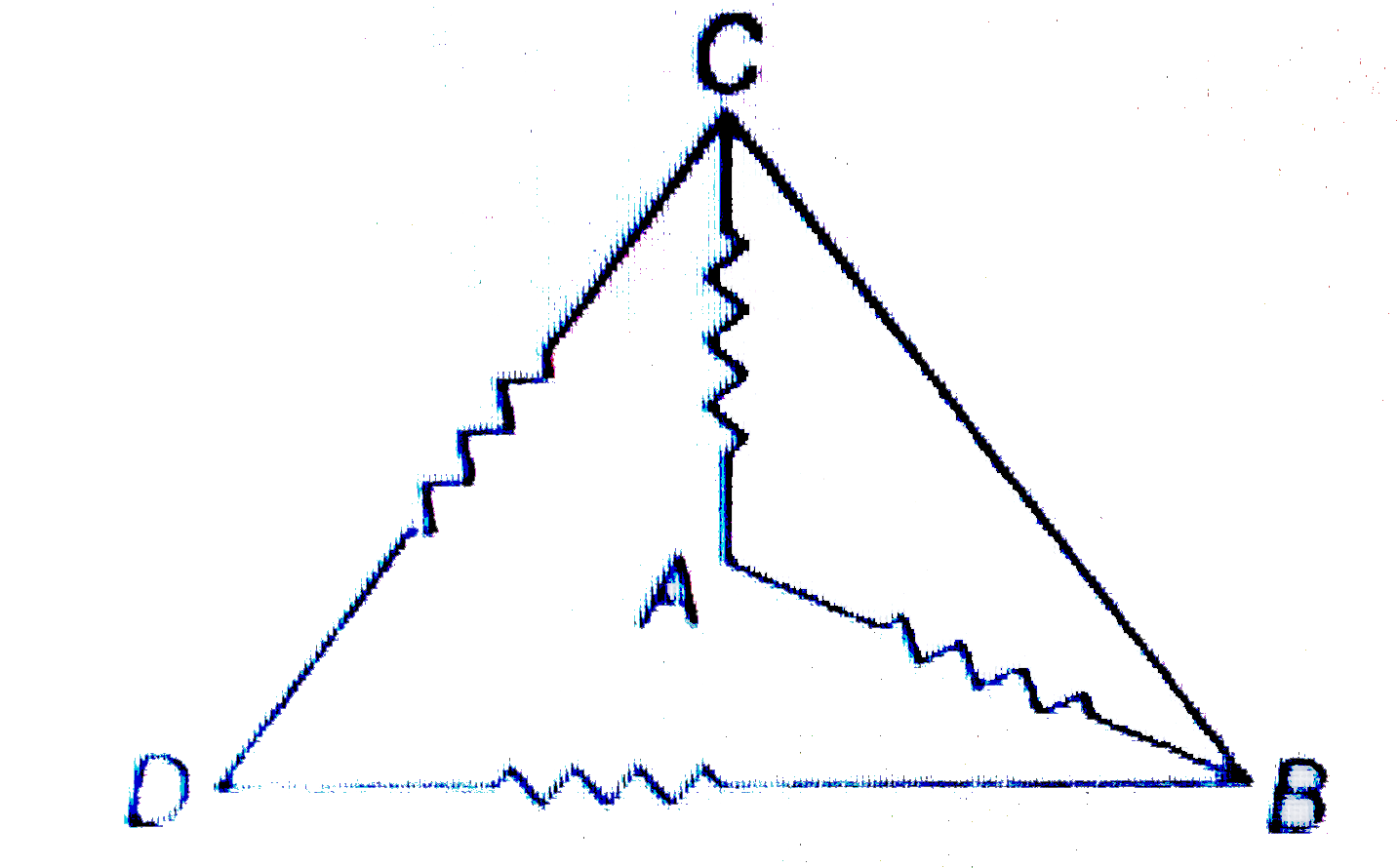
View SolutionA wire is bent in the form of a triangle now the equivalent resistance between its one end and the mid point of the side is
View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is

View SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
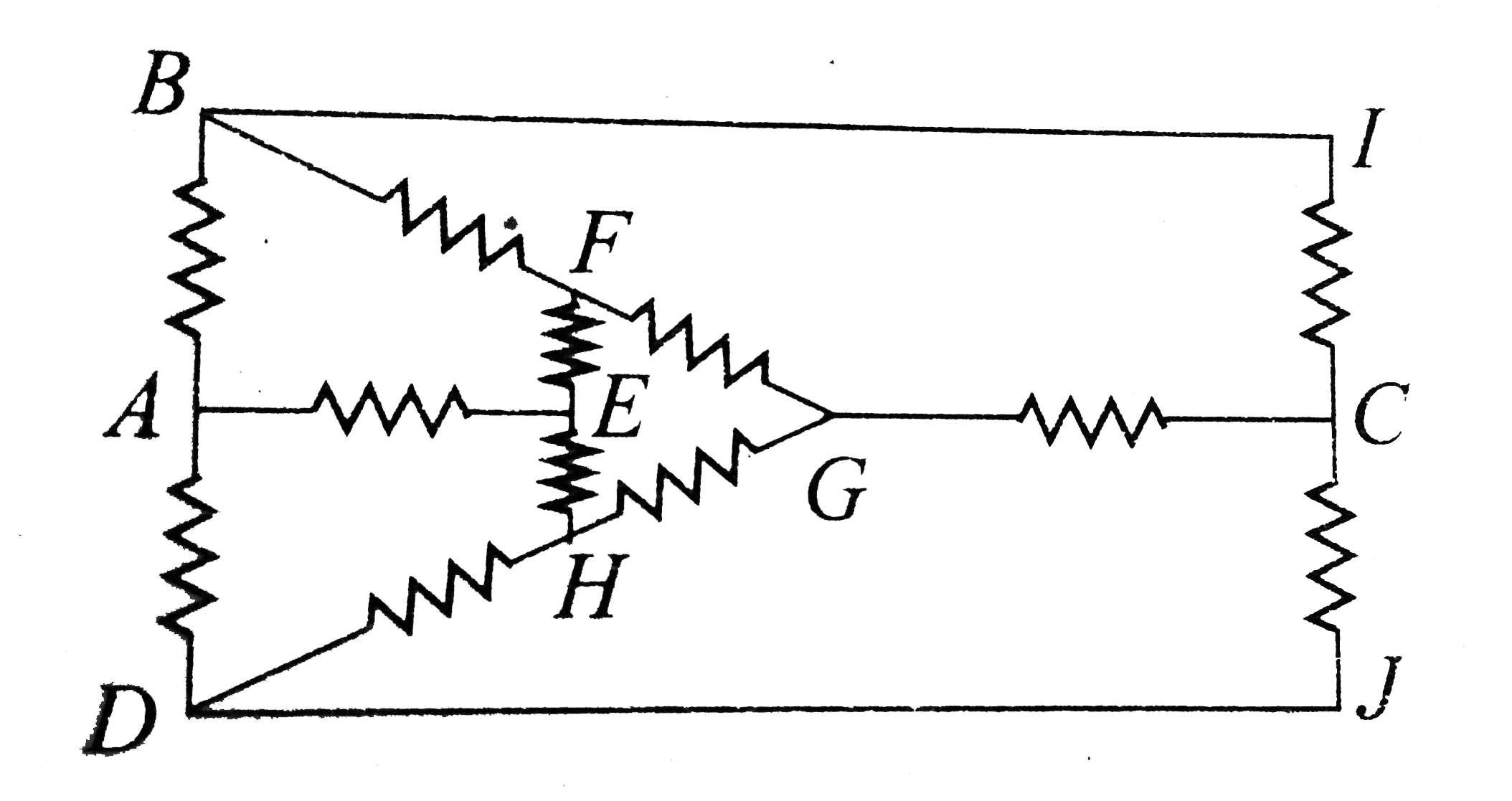
View Solutionfind the equivalent resistance between A and E(resistance of each resistor is R.
View Solution
