If Bohar 's quantisation postulate ( angular momentum = nh/2π) is a basic law of nature , it should be equal be equally valid for the case of planetary motion also . Why then do we never speak of quatisation of orbit of planets around the Sun ?
If we try to apply Bohr.s quantum conditions to planetary motion then on calculating angular momentum of planet we find the value of angular momentum is incomparably large relative to Planck.s constant h. For earth , it is such that quantum number n =1070 .For such large values of n, the difference in the successive energies and angular momenta of the quantised levels of the Bohr model are so small that of all purpose we may consider the angular momentum as well as energy levels continuous.
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - CASE BASED/SOURCE - BASED INTERGRATED QUESTIONS10videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - MULTIPLE CHOICE QUESTIONS30videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SELF ASSESSMENT TEST (SECTION C)2videos
ATOMS
- BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - SELF ASSESSMENT TEST (SECTION -C)2videos
ALTERNATING CURRENT
- BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION D12videos
CBSE EXAMINATION PAPER 2020
Similar Questions
If Bohr’s quantization postulate (angular momentum = nh/2π ) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?
View SolutionIf Bohr's qunatisation postulate (angular momentum=nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do never speak of quantization of orbits of planets around the sun?
View Solution
Knowledge Check
- Question 1 - Select One
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
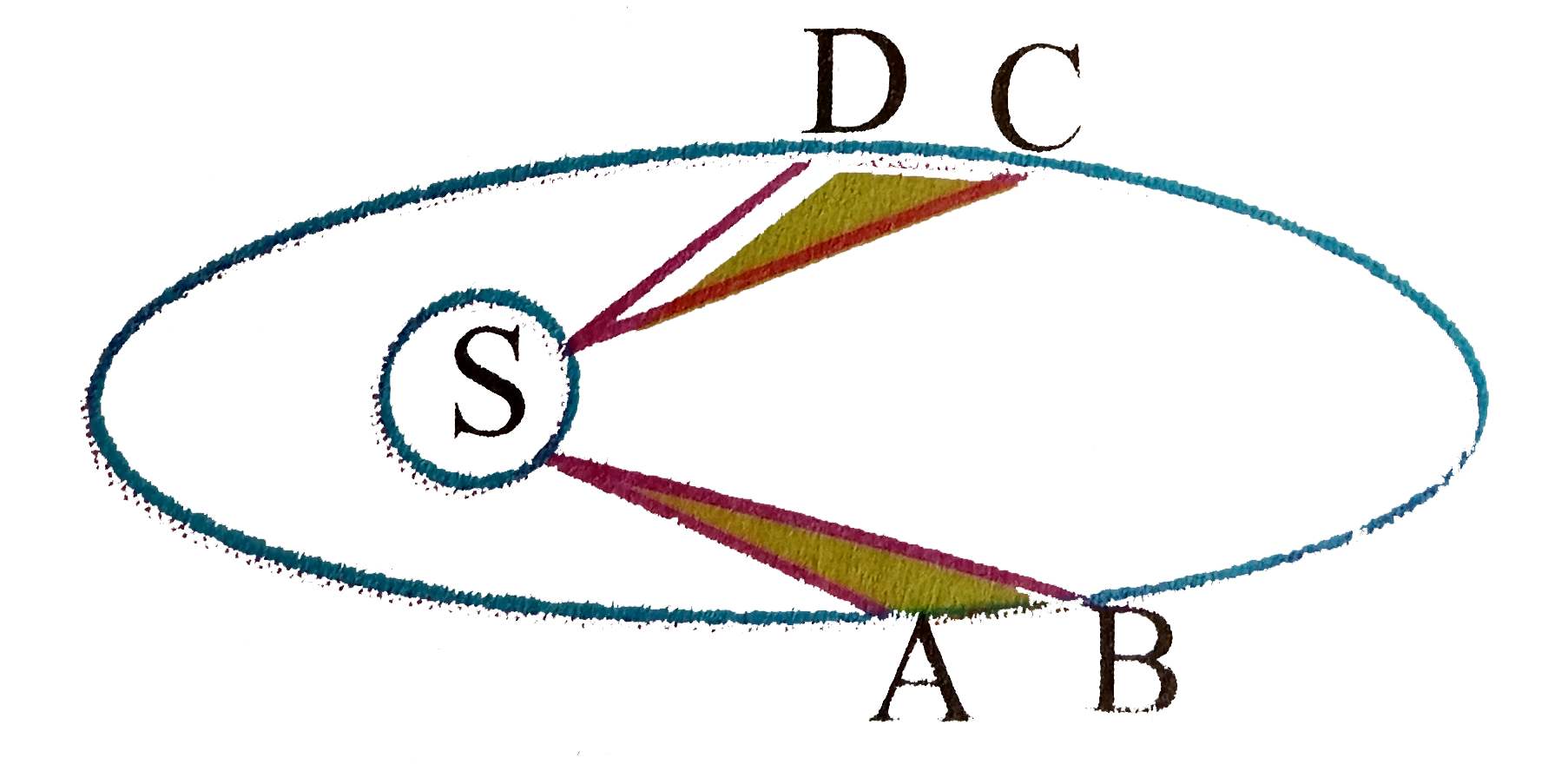 A3GMmaB5GMmaCGMmaDnone of the above
A3GMmaB5GMmaCGMmaDnone of the above - Question 2 - Select One
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
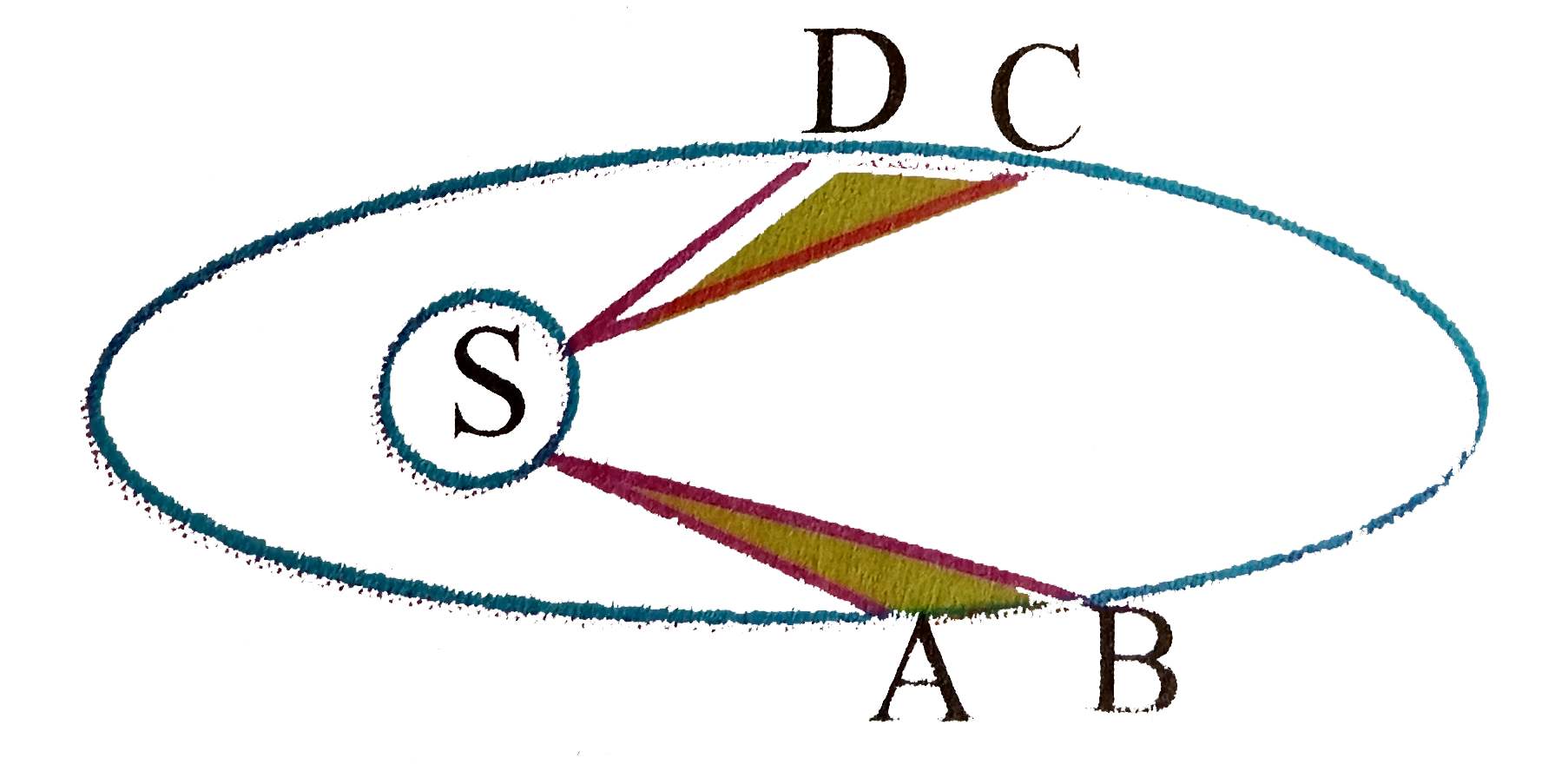 A−3GMm4aB−3GMm8aC−GMm5aDnone of these
A−3GMm4aB−3GMm8aC−GMm5aDnone of these - Question 3 - Select One
It is tempting to think that all possible transition are permissible and that an atomic spectrum arises from the transition of an electron from any initial orbital to any other orbital .However this is not so because a photon a photon has as intrinsic spin angular momentum of √2h/2π corresponding to S=1 although it has no charge and no rest mass
On the other hand , an electron has got two type of angular momentum: orbital angular momentum
L=[√l(l+1)]h/2π,and spin angular momentum L1=√s(s+1)h/2π arising from orbital motion and spin motion of the electron during any electronic transition must compensate for the angular momentum carried away by the photon .To satisfy this condition the different between the azimuthal quantum number of the orbital within which the transition take place must differ by 1.thus, an electron in a d-orbital (l=2) cannot make a transition into as s-orbital (l=0)because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electron with n=5 isA√2h2πB√6h2πC√12h2πD√20(h2π)
While studying the theory of planetary motion, kepler established three laws. According to kepler's second law, the line joining a planet to the sun sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant. This led him to conlude from the sun.
Read the above passege and answer the following questions :
(i) What is the basis of kepler's second law?
(ii) Mercury is closer to the sun than the earth. Will time period of mercury be less or more than one year ? Why ?
(iii) What value of life do you learn from kepler's second law?View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
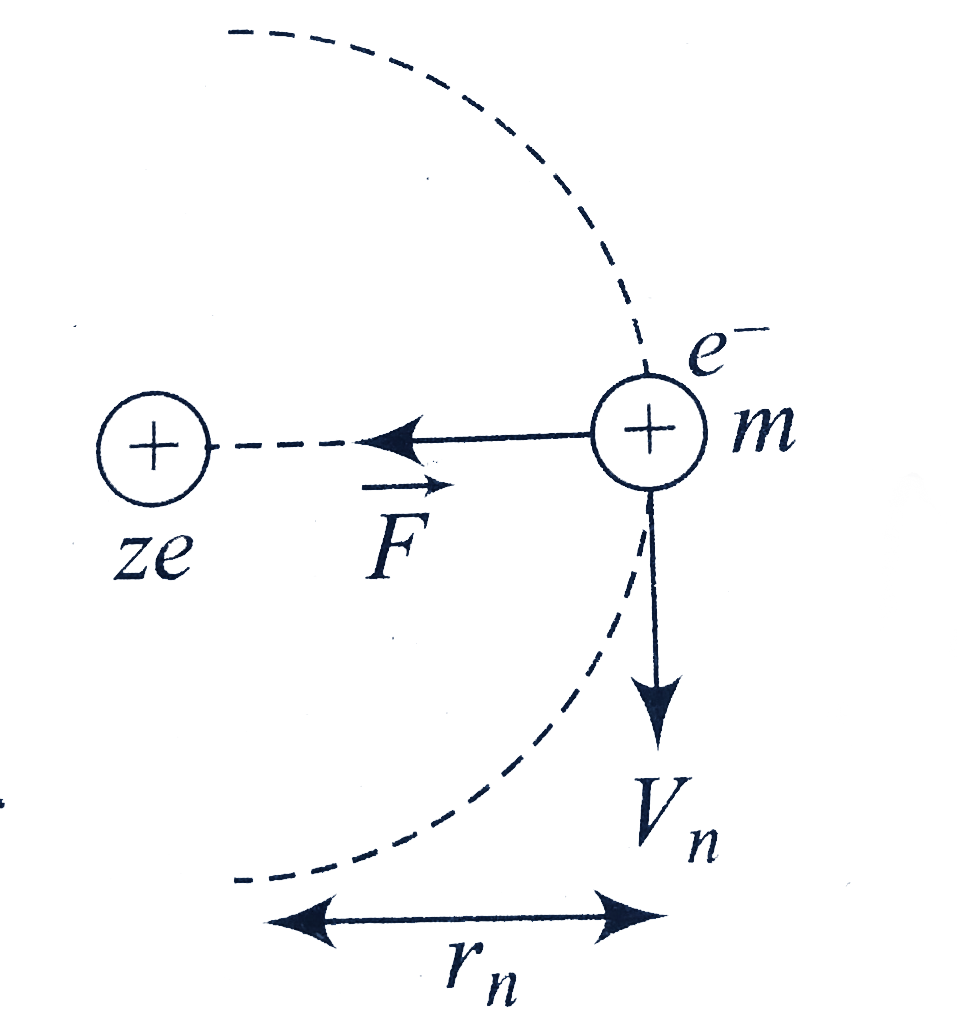
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.

we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
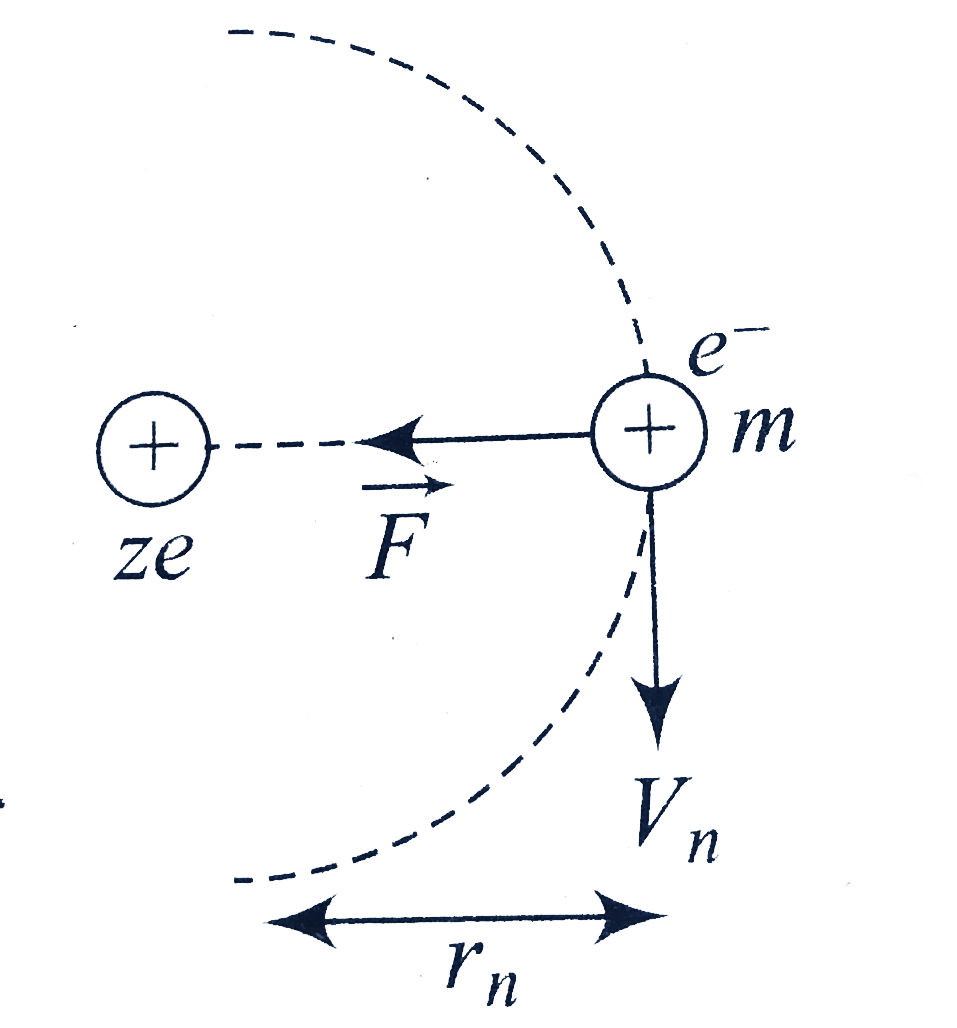
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multiple of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will beView SolutionL=√l(l+1)h2π
On the other hand, m determines Z-component of orbital angular momentum as Lz=m(h2π)
Hund's rule states that in degenerate orbitals electron s do not pair up unless and until each such orbital has got an electron with parallel spins. Besides orbital motion, an electron also possess spin-motion. spin may be clockwise and anti-clockwise. Both thes spin motions are called two spin states of electron characterised by spin. s=+12 and s=−12, respectively.
The orbital angular momentum of electron (l=1) makes an angle of 45∘ from Z-axis. The Lz of electron will beView Solution

