Question

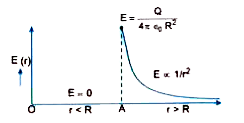
Use Gauss's law to show that due to uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for ${\displaystyle r\le R}$ and ${\displaystyle r\ge R}$.

Explanation

Consider a uniformly charged thin spherical shell of radius R and having a charge Q. To find electric field at a point P outside the shell situated at a distance `r(r gt R)` from the centre of shell, consider a sphere of radius r as the Gaussian surface. All points on this surface are equivalent relative to given charged shell and, thus, electric field `vecE` at all points of Gaussian surface has same magnitude `vecE` and `hatn` are parallel to each other.

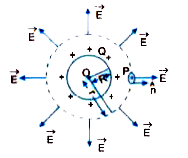
`therefore ` Total electric flux over the Gaussian surface
`phi_(E )= int vecE. hatn ds=E.4pi r^(2)" " ...(i)`
According to Gauss.s theorem,
`phi_(E )=(1)/(in_(0))"(charge enclosed)"=(Q)/(in_(0))" " ...(ii)`
Comparing (i) and (ii), we get
`E.4pi r^(2)=(Q)/(in_(0)) or E=(Q)/(4pi in_(0)r^(2))`.
Thus, for any point outside the shell, the effect is, as if whole charge Q is concentrated at the centre of the spherical shell.
A graph showing the variation of electric field E with r has been plotted here.